基于邊際-人工蜂群算法的艦載機機群出動保障人員配置-調(diào)度聯(lián)合優(yōu)化方法
蘇析超,伍恒,崔榮偉,張勇
(1.海軍航空大學,煙臺264001; 2.海軍研究院,北京100191)
艦載機機群出動保障是全周期出動回收作業(yè)的關(guān)鍵階段,作為衡量出動回收能力的核心指標,保障效率的發(fā)揮不僅與航母航空保障系統(tǒng)的指揮調(diào)度和協(xié)調(diào)控制水平密切相關(guān)[1],同時受限于以保障人員為主體的各類保障資源的規(guī)模和能力[2]。相對于陸基機場,甲板空間狹小、安全態(tài)勢復雜,傳統(tǒng)的固定機組制人員利用率較低,人數(shù)需求隨著機群規(guī)模增加而線性遞增,無法滿足艦載航空保障“減員增效”的要求;另外,當前國內(nèi)外航母艦載機調(diào)度仍處在以人工經(jīng)驗為主的水平,在大規(guī)模機群保障條件下難以確保最優(yōu)調(diào)度性能。因此,基于一體化聯(lián)合保障模式和智能調(diào)度技術(shù),開展面向出動任務(wù)的保障人員配置和資源分配調(diào)度聯(lián)合優(yōu)化,是高強度、快節(jié)奏作戰(zhàn)訓練條件下艦載機指揮管理信息化和智能化的迫切需求和發(fā)展趨勢。
由于艦載機出動保障作業(yè)內(nèi)涵開放性不足,約束限制多,研究難度大,當前國內(nèi)外針對出動保障調(diào)度和人員配置的研究成果尚不充分。在出動保障調(diào)度方面,Ryan等[3]基于所開發(fā)的甲板作業(yè)規(guī)劃決策系統(tǒng)(Deck operations Course of Action Planner,DCAP)[4],對比了專家經(jīng)驗和基于整數(shù)線性規(guī)劃的自動決策方法的優(yōu)劣。文獻[5]面向一站式保障調(diào)度問題,構(gòu)建了艦載機艦面機務(wù)勤務(wù)保障的資源受限項目調(diào)度模型;文獻[6]則借鑒柔性車間調(diào)度問題,對艦載機甲板作業(yè)進行建模優(yōu)化分析。文獻[7-8]以甲板空間約束為出發(fā)點,分別研究了考慮停機位空間約束的保障組調(diào)度和考慮調(diào)運/作業(yè)空間約束的艦載機作業(yè)調(diào)度。文獻[9]基于分布式路徑規(guī)劃方法,解決了出動階段的協(xié)同調(diào)度問題。文獻[10]進一步考慮了作業(yè)時間的不確定性,構(gòu)建了前攝式艦面保障調(diào)度優(yōu)化模型。以上研究不斷朝著約束的復雜化、模型的精細化和目標的多樣化發(fā)展。
在艦載機保障人員配置優(yōu)化方面,Ross[2]基于多主體(Multi-agent)仿真技術(shù),研究了保障人員配置數(shù)量與艦載機出動效率的影響關(guān)系;文獻[11]在多主體架構(gòu)基礎(chǔ)上,內(nèi)嵌合同網(wǎng)協(xié)議,提出了面向艦載機故障維修的保障人員配置和任務(wù)分配模型。崔博[12]提出了艦載機保障人員技能分配優(yōu)化方法,并采用遞增遍歷算法確定保障組人數(shù)。郭小威等[13]針對工時不確定下的航空彈藥保障作業(yè),以基于蒙特卡羅的PERT網(wǎng)絡(luò)仿真為效能評估核心,外層以遺傳算法為優(yōu)化框架,對保障人員配置方案進行優(yōu)化。針對資源配置的方法研究[14]在裝備保障領(lǐng)域可以歸納為經(jīng)驗比例公式[15]、數(shù)學規(guī)劃[16]、基于排隊模型的優(yōu)化方法[17]和基于蒙特卡羅仿真的優(yōu)化方法[18]等;按照資源配置主體,又區(qū)分為人員設(shè)備等可更新資源和不可修備件等消耗性資源。其中,邊際優(yōu)化算法作為一種高效實用的方法,在備件配置優(yōu)化領(lǐng)域得到了廣泛應(yīng)用[19]。
綜上所述,現(xiàn)有研究主要存在2個方面不足:①艦載機出動保障調(diào)度優(yōu)化和保障人員配置優(yōu)化的研究相對獨立,缺乏聯(lián)合優(yōu)化的機制;②當前調(diào)度模型的研究較少考慮資源轉(zhuǎn)移過程,更沒有細化至保障工位之間轉(zhuǎn)移,難以實現(xiàn)精細化保障需求。據(jù)此,本文立足艦載機出動任務(wù)需求,在一體化聯(lián)合保障模式下,構(gòu)建艦載機機群出動保障的人員配置和調(diào)度的聯(lián)合優(yōu)化模型,并提出基于邊際-人工蜂群(Artificial Bee Colony,ABC)算法的兩層優(yōu)化決策架構(gòu)進行模型求解,以實現(xiàn)艦載機機群出動保障的人員配置和調(diào)度決策的集成,減少決策環(huán)節(jié),進一步促進艦載航空保障的“減員增效”。
1 問題描述
艦載機機群出動保障人員配置與調(diào)度聯(lián)合優(yōu)化問題(Integrated Staffing and Scheduling Problem for Aircraft Sortie Support,ISSP-ASS)的目標是確定各專業(yè)保障人員數(shù)量及各類人員設(shè)備的分配計劃保障時序,以滿足出動時間的要求。與傳統(tǒng)的固定機組制不同,一體化聯(lián)合保障模式下各專業(yè)保障人員可在各架同機型艦載機之間轉(zhuǎn)移保障,因此可最大程度地提升保障人員利用率。該模式主要應(yīng)用于美軍艦載機保障,對人員配置和管理調(diào)度提出了更高要求。在給定保障人員配置方案下,保障資源的調(diào)度則受限于出動保障流程約束、出動時限約束、保障人員約束、保障設(shè)備約束、工位空間約束和資源供給能力約束等條件。
傳統(tǒng)任務(wù)規(guī)劃模式下,保障人員配置和保障作業(yè)調(diào)度兩者為先后序決策,即一般先根據(jù)保障任務(wù)量,基于經(jīng)驗進行人力資源的配置,或直接指派在位的所有員額,再根據(jù)人力資源進行保障方案的規(guī)劃調(diào)度。然而保障人員的配置直接影響到調(diào)度性能,獨立的分步?jīng)Q策可能導致調(diào)度方案無法滿足指標要求。因此,需要將2項決策任務(wù)進行統(tǒng)籌考慮和建模。

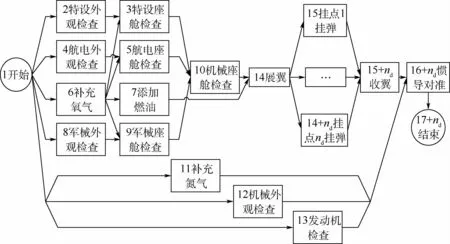
圖1 單機出動保障作業(yè)流程圖Fig.1 Support operation flowchart for single-aircraft sortie
每一架飛機均有各自的入場時間Mi,表示第i架飛機調(diào)運至停機位pi,并系留完畢,這也是單機保障的最早可開始時刻。令Oij表示第i架飛機的第j道工序,該工序當且僅當其前序工序集Pij均保障完畢后方可開始作業(yè),保障所需工時為dij,保障所屬工位表示為Wij。假設(shè)機群出動保障滿足“一站式”條件[5],即各艦載機在任一停機位均可滿足所有資源的保障,可原位保障所有工序。每項工序可能涉及至多4類資源需求:保障人員、保障設(shè)備、工位空間和供給類資源,其各自種類集合分別定義為Kp、Ke、Ks和Kw。

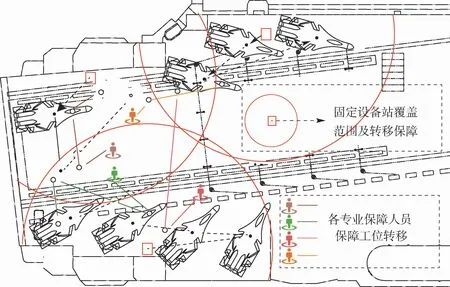
圖2 保障人員和設(shè)備轉(zhuǎn)移保障示意圖Fig.2 Schematic diagram of support personnel and equipment transfer
2 ISSP-ASS模型
2.1 決策變量和優(yōu)化目標建立
ISSP-ASS模型需優(yōu)化生成艦載機機群出動保障人員的數(shù)量配置、各保障人員設(shè)備的工序分配及作業(yè)時序等具體保障方案,因此模型的決策變量定義為



對2個優(yōu)化目標按照字典序進行排序,即優(yōu)先確保保障人員數(shù)量最小化,其次優(yōu)化人員負載均衡性,實際運算中可采用加權(quán)的形式進行組合。
2.2 數(shù)學模型建立
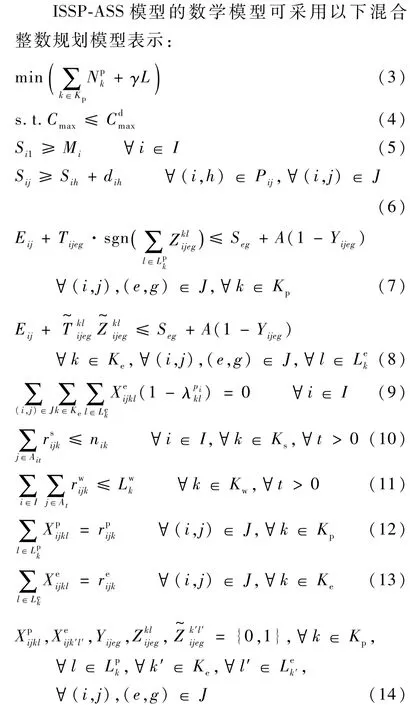


3 聯(lián)合優(yōu)化方法設(shè)計
針對第2節(jié)ISSP-ASS優(yōu)化問題,最直接的求解思路是采用集成式優(yōu)化方法,即將保障人員配置和保障作業(yè)調(diào)度作為一體化并列的決策對象,并同步開展迭代優(yōu)化。該方法的優(yōu)勢在于:算法設(shè)計簡單,只需采用一種優(yōu)化算法對配置和調(diào)度進行統(tǒng)一的編碼、解碼和循環(huán)搜索迭代。然而,人員配置和作業(yè)調(diào)度2部分的決策變量存在一定遞階關(guān)聯(lián)性,即最優(yōu)調(diào)度方案取決于人員的配置。如果同步對2部分決策變量進行擾動搜索,一方面2部分決策變量組合的搜索空間浩大,難以收斂至較優(yōu)解區(qū)域,尋優(yōu)的魯棒性難以保證;另一方面,搜索缺乏導向性,容易形成無效搜索,如針對局部最優(yōu)解,如果對2部分決策變量同步進行擾動尋優(yōu),則可能完全破壞原解的結(jié)構(gòu),無法在當前人員配置下進一步局部優(yōu)化調(diào)度方案。
為有效利用保障人員配置和調(diào)度方案的遞階關(guān)聯(lián)關(guān)系,提升尋優(yōu)的針對性和搜索效率,可采用兩層決策機制進行求解。在兩層規(guī)劃模型中,上下層均包含完整的目標和約束模型,下層模型依據(jù)上層模型的優(yōu)化參數(shù)來引導自身目標優(yōu)化,上層則依賴下層的優(yōu)化反饋來優(yōu)化自身目標。應(yīng)用至本文問題,構(gòu)建兩層決策模型的概念圖如圖3所示。
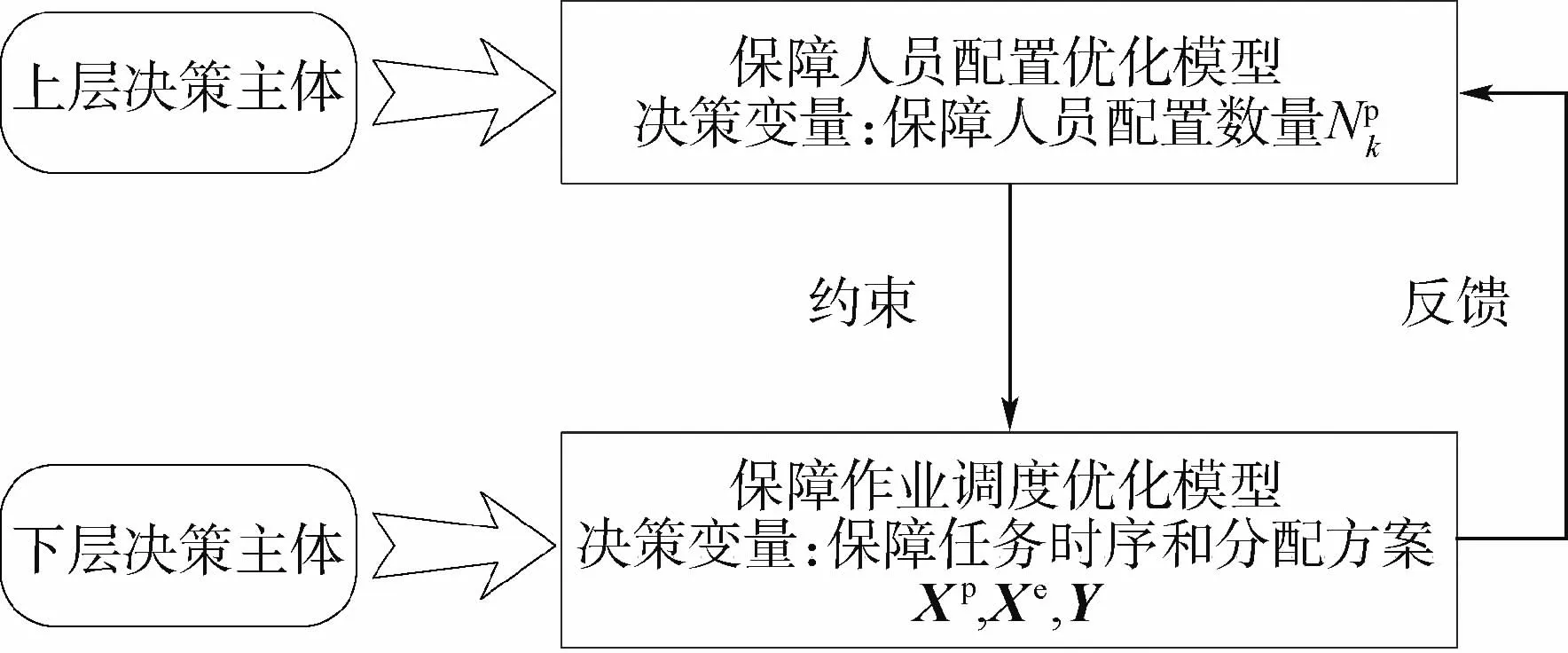
圖3 求解ISSP-ASS的兩層決策模型概念圖Fig.3 Concept of bi-level decision model for ISSP-ASS
上層模型負責各專業(yè)保障人員的配置決策。對此,采用邊際優(yōu)化算法進行求解,該算法操作簡單,搜索精度高,且最大優(yōu)勢在于迭代過程不丟失最優(yōu)解,在求解資源配置這類問題相對一般啟發(fā)式算法更具優(yōu)勢。下層模型負責艦載機機群出動保障調(diào)度優(yōu)化,以縮短保障完工時間,本文設(shè)計了一類改進人工蜂群算法進行求解。在每一步迭代過程中,在上層將各類專業(yè)保障人員分別增加單位數(shù)量后,調(diào)用下層調(diào)度優(yōu)化模型計算邊際效益的增量,下層則根據(jù)所增加的保障人員配置,基于改進的人工蜂群算法求解最優(yōu)調(diào)度方案,并將機群保障完工時間和保障人員負載方差和反饋至上層配置模型,由上層模型選取邊際效益最優(yōu)的人員增加方案,通過不斷迭代直至滿足機群完工時間的時限要求。基于邊際-人工蜂群算法的艦載機機群出動保障人員配置-調(diào)度聯(lián)合優(yōu)化流程如圖4所示。
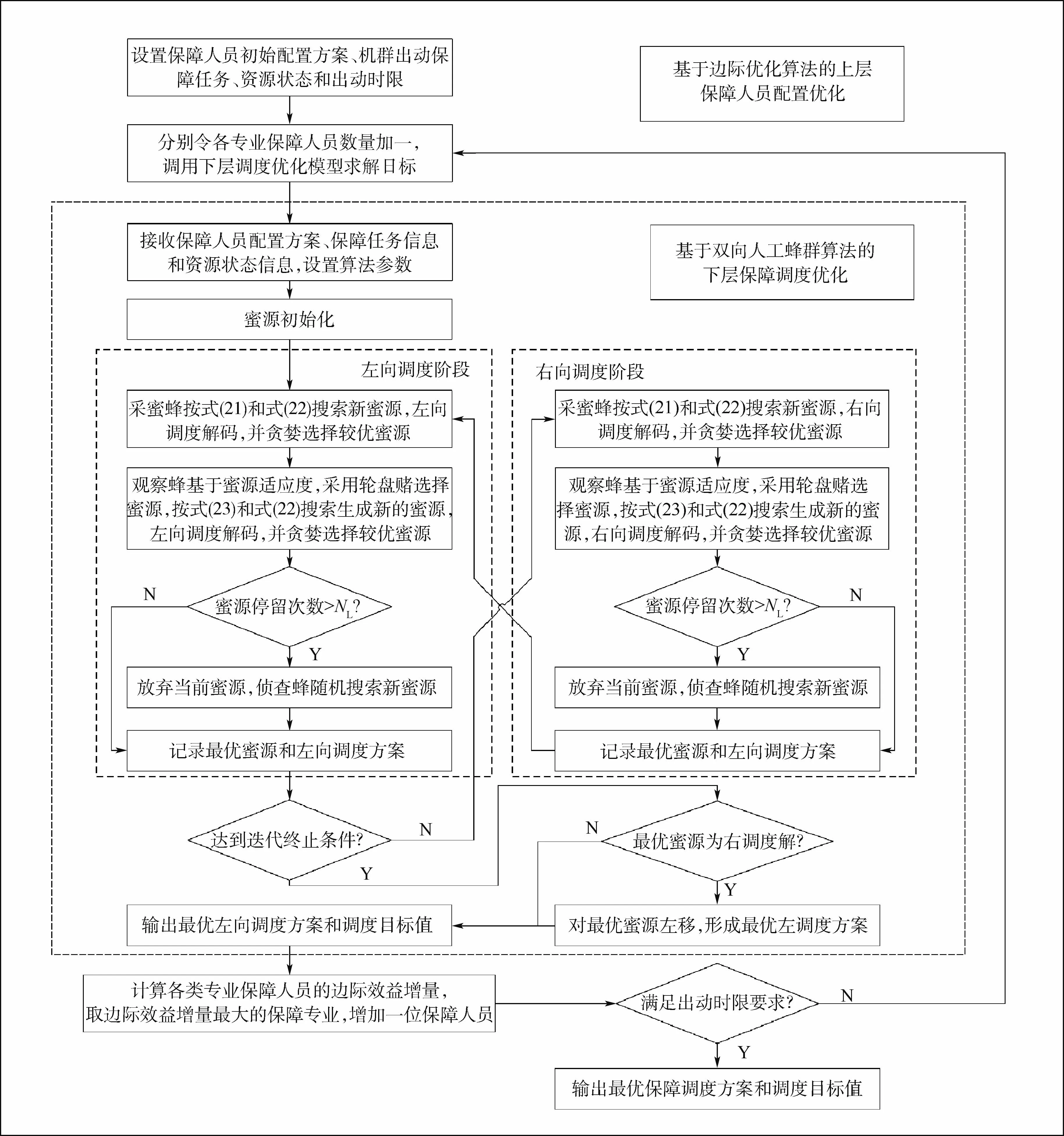
圖4 邊際-人工蜂群算法流程Fig.4 Marginal-ABC algorithm flowchart
3.1 上層保障人員配置優(yōu)化
保障人員的數(shù)量配置直接影響了機群保障完工時間,當保障人員數(shù)量較少時,保障完工時限約束(4)未必得到滿足,因此上層決策的目標是在保證達到保障完工時限的要求前提下,優(yōu)化目標函數(shù)(3),因此,上層保障人員配置優(yōu)化模型可抽象為
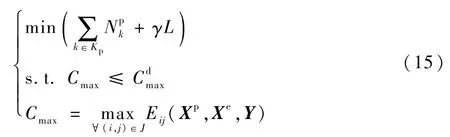
式中:(Xp,Xe,Y)表示機群保障調(diào)度分配決策方案。
采用邊際優(yōu)化算法,可將該優(yōu)化問題轉(zhuǎn)化為:依據(jù)各專業(yè)保障人員數(shù)量的邊際效益增量大小,選取專業(yè)類別進行逐項增加的方式,使得機群完工時間不斷迭代壓縮至完工期限內(nèi)。因此,可將第g次迭代過程中第k(k∈Kp)類專業(yè)保障人員的邊際效益增量定義為

在統(tǒng)一的調(diào)度優(yōu)化算法和較高的優(yōu)化魯棒性條件下,機群保障調(diào)度完工時間是關(guān)于保障人員配置數(shù)量的遞減函數(shù),考慮到α為極小值,第二目標項對優(yōu)化目標函數(shù)值的影響較小,因此可將目標函數(shù)近似看做凸函數(shù),即滿足邊際優(yōu)化需假設(shè)目標函數(shù)為凸的前提條件。
基于邊際優(yōu)化算法的上層保障人員配置優(yōu)化基本步驟如下:


式中:第k(k∈Kp)類專業(yè)保障人員的初始配置數(shù)量與配置強度、所保障工序的工作量成正比,與出動保障時限成反比。其中保障人員配置強度R為變量,隨著R增加,各專業(yè)保障人員數(shù)量按比例遞增。由于保障調(diào)度的復雜性,式(17)所得初始保障人員配置的比例未必是最優(yōu)比例,因此R的賦值不宜過大以免超出最優(yōu)保障配置解。

3.2 下層保障調(diào)度配置優(yōu)化
下層決策以上層保障人員配置作為輸入,求解以機群出動保障完工時間和負載方差和最小化為目標的保障工序任務(wù)分配及保障時序方案。因此,下層保障調(diào)度優(yōu)化模型可概括為

該問題可抽象為考慮轉(zhuǎn)移時間的資源約束下多項目調(diào)度問題(Resource-Constrained Multi-Project Scheduling Problem with Transfer Times,RCMPSPTT)[20]。由于RCMPSPTT的NP-hard特性,精確算法難以求解其中大規(guī)模調(diào)度問題,而以人工蜂群[21]算法為代表的元啟發(fā)式算法則可實現(xiàn)求解效率和求解精度之間的權(quán)衡,并在調(diào)度領(lǐng)域中得到了廣泛應(yīng)用。采用該算法求解本文調(diào)度問題的考慮在于:①算法控制參數(shù)少,易于操作;②采蜜蜂和觀察蜂的搜索機制較好地實現(xiàn)全局和局部搜索的協(xié)調(diào);③偵察蜂機制可有效避免陷入局部極值,更適用于ISSP-ASS這類多峰優(yōu)化問題的求解。
經(jīng)典的人工蜂群算法的搜索策略僅針對一維的局部搜索,搜索能力有限,對于大規(guī)模調(diào)度這類多維優(yōu)化問題會出現(xiàn)收斂速度較慢的現(xiàn)象。對此,本文在基本人工蜂群算法架構(gòu)之上,引入差分進化的交叉變異策略以提升蜂群的搜索效率,并將項目調(diào)度中的面向個體解的雙向?qū)R局部搜索[22]轉(zhuǎn)換為面向種群的雙向?qū)R,進一步提升種群的優(yōu)化性能。本文改進的雙向人工蜂群算法流程如圖4所示,具體執(zhí)行步驟如下:
步驟1 接收上層決策中的艦載機機群出動保障任務(wù)、保障人員配置等資源狀態(tài)及相關(guān)信息;設(shè)置蜜源數(shù)目NS,蜜源停留最大限制搜索次數(shù)NL,初始化隨機生成NS個蜜源。
步驟2 執(zhí)行基于左向調(diào)度的人工蜂群搜索,按以下子步驟進行:
步驟2.1 采蜜蜂按式(21)和式(22)搜索生成新的蜜源,基于左向調(diào)度求解其適應(yīng)度,并貪婪選擇較優(yōu)蜜源。
步驟2.2 觀察蜂根據(jù)蜜源花蜜量信息,基于輪盤賭概率選擇一個蜜源,并按式(23)和式(22)搜索生成新的蜜源,同理基于左向調(diào)度求解其適應(yīng)度,并貪婪選擇較優(yōu)蜜源。
步驟2.3 若蜜源停留次數(shù)超過NL,則放棄該蜜源,同時該處的采蜜蜂轉(zhuǎn)變偵察蜂,隨機搜索新蜜源。
步驟3 判斷是否達到最大評價次數(shù),若是,則終止迭代,并輸出最優(yōu)的艦載機機群出動保障的人員、設(shè)備分配方案和保障時序計劃;若未達到迭代終止條件,則轉(zhuǎn)入步驟4繼續(xù)迭代優(yōu)化。
步驟4 執(zhí)行基于右向調(diào)度的人工蜂群搜索,具體搜索子步驟與步驟2相同,其中差別在于生成的新蜜源采用右向調(diào)度進行適應(yīng)度的評價。轉(zhuǎn)入步驟2繼續(xù)迭代優(yōu)化。
步驟5 判斷最優(yōu)解對應(yīng)的調(diào)度方式,若為右向調(diào)度,則保持資源分配固定,對右向調(diào)度解左移生成左向最優(yōu)調(diào)度方案。
3.2.1 蜜源編碼形式
種群中每個蜜源個體對應(yīng)一個調(diào)度解,一方面為了利用人工蜂群算法求解連續(xù)優(yōu)化問題的優(yōu)勢,另一方面為了實現(xiàn)編碼與解空間的一對一映射,以精簡搜索空間,同時是為了便于基于種群的雙向?qū)R調(diào)度。本文設(shè)計了基于保障工序開始和結(jié)束時間向量的拓展優(yōu)先序編碼。
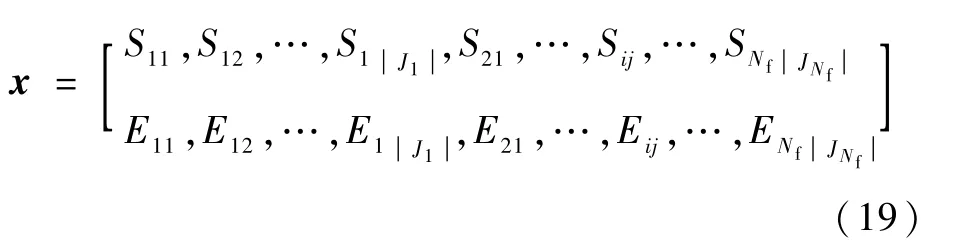
該編碼為兩層結(jié)構(gòu),第1行是保障工序開始時間向量,作為用于生成左向調(diào)度時的優(yōu)先序列表,取值越小則調(diào)度優(yōu)先級越高;第2行是保障工序結(jié)束時間向量,作為用于生成右向調(diào)度時的優(yōu)先序列表,取值越大則調(diào)度優(yōu)先級越高。在每次解碼的調(diào)度方案生成后,將新的時序方案修正原編碼。
3.2.2 解碼調(diào)度過程
本節(jié)以左向調(diào)度為例,右向調(diào)度過程為左向調(diào)度的逆方向過程。采用串行調(diào)度生成機制,定義已完成調(diào)度工序集Sg,可調(diào)度工序集Dg,解碼調(diào)度過程是從Dg中按工序優(yōu)先級選取工序,并安排在滿足各項約束的最早可開工時刻,分配人員、設(shè)備資源,并加入集合Sg這一循環(huán)迭代過程。將時間離散化,取間隔為Δt=0.1,解碼調(diào)度具體執(zhí)行步驟如下:
步驟6 為工序分配資源,從滿足工位轉(zhuǎn)移時序約束的保障人員集合中,選擇負載Bkl最小所對應(yīng)的保障人員;從滿足工位轉(zhuǎn)移時序約束的保障設(shè)備集合中,根據(jù)MTRCA規(guī)則[5],選擇覆蓋范圍內(nèi)剩余工序作業(yè)時間最少的保障設(shè)備進行分配,更新所分配保障人員和設(shè)備的保障作業(yè)狀態(tài),令Sg=Sg∪(i*,j*),轉(zhuǎn)入步驟2執(zhí)行下一個工序調(diào)度。
步驟7 輸出保障時序計劃和保障人員、設(shè)備的工序分配方案,根據(jù)式(18)計算目標函數(shù)值。
基于解碼調(diào)度結(jié)果,機群保障完工時間越短,保障人員負載方差和越小,則蜜源的花蜜量(適應(yīng)度)越大,因此算法的花蜜量可表示為
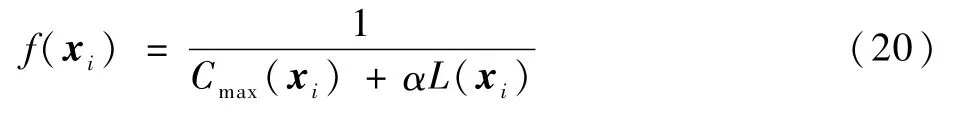
3.2.3 蜜源位置更新策略
在進行蜜源位置更新時,分為左向調(diào)度階段和右向調(diào)度階段。在左向調(diào)度時,取各蜜源位置的保障工序開始時間向量構(gòu)成的種群xL作為更新對象;反之在右向調(diào)度時,取保障工序結(jié)束時間向量構(gòu)成的種群xR作為更新對象。以下以左向調(diào)度階段為例,右向調(diào)度階段的蜜源更新操作與之相同。


當蜜源停留次數(shù)達到限制NL后,則放棄該蜜源,并由偵察蜂隨機產(chǎn)生一個新的蜜源,從而防止蜜源個體陷入局部極值,并增強種群多樣性。
3.2.4 面向種群的雙向?qū)R機制
面向種群的雙向?qū)R機制將進化過程分為了左向調(diào)度階段和右向調(diào)度階段,2類調(diào)度機制可有助于彼此時序的微調(diào)優(yōu)化以進一步壓縮工期。通過引入該機制,使得算法在2個方面得到改進:
1)經(jīng)典的雙向?qū)R技術(shù)針對個體調(diào)度方案進行,并將消耗更多額外的計算量,因此往往僅針對部分較優(yōu)個體實施;而面向種群的雙向?qū)R則將該機制融入到人工蜂群的進化過程,節(jié)省計算量的同時也將應(yīng)用范圍拓展到整個群體。
2)通過種群的交替雙向迭代,可增強蜜源位置(基因)的多樣性,有助于克服由于單一方向調(diào)度導致的早熟及陷入局部極值的問題。
4 算例仿真與分析
4.1 出動案例構(gòu)建

表1中,各項保障工序?qū)ΡU先藛T和設(shè)備的需求單位均為1。保障人員專業(yè)種類按特設(shè)、航電、軍械和機械依次編號1~4;保障設(shè)備種類按加油站、電源站、充氧站、充氮站、液壓站、掛彈設(shè)備和慣導對準裝置依次編號1~7;工位空間僅列出存在限制的座艙空間,僅可容納一人進行保障作業(yè);供給性資源種類對應(yīng)設(shè)備種類進行編號,且供給限制為[Lw1,Lw2,Lw3,Lw4,Lw5]=[5,8,2,4,6]。

表1 保障工序?qū)ΡU腺Y源需求Table 1 Support resource demand of support operations
4類作戰(zhàn)任務(wù)對應(yīng)的保障工序工時如表2所示。保障人員和保障設(shè)備在各機工位間轉(zhuǎn)移時間規(guī)模較大,篇幅原因不在文中列出。
甲板上各類保障設(shè)備的可覆蓋保障飛機集合如表3所示。表3中,1~5類保障設(shè)備均為固定設(shè)備站,除表3中所示,掛彈設(shè)備為移動保障設(shè)備,可覆蓋全甲板保障,配置12組,慣導對準設(shè)備較充足,不會對保障造成約束,因此本文案例可忽略。
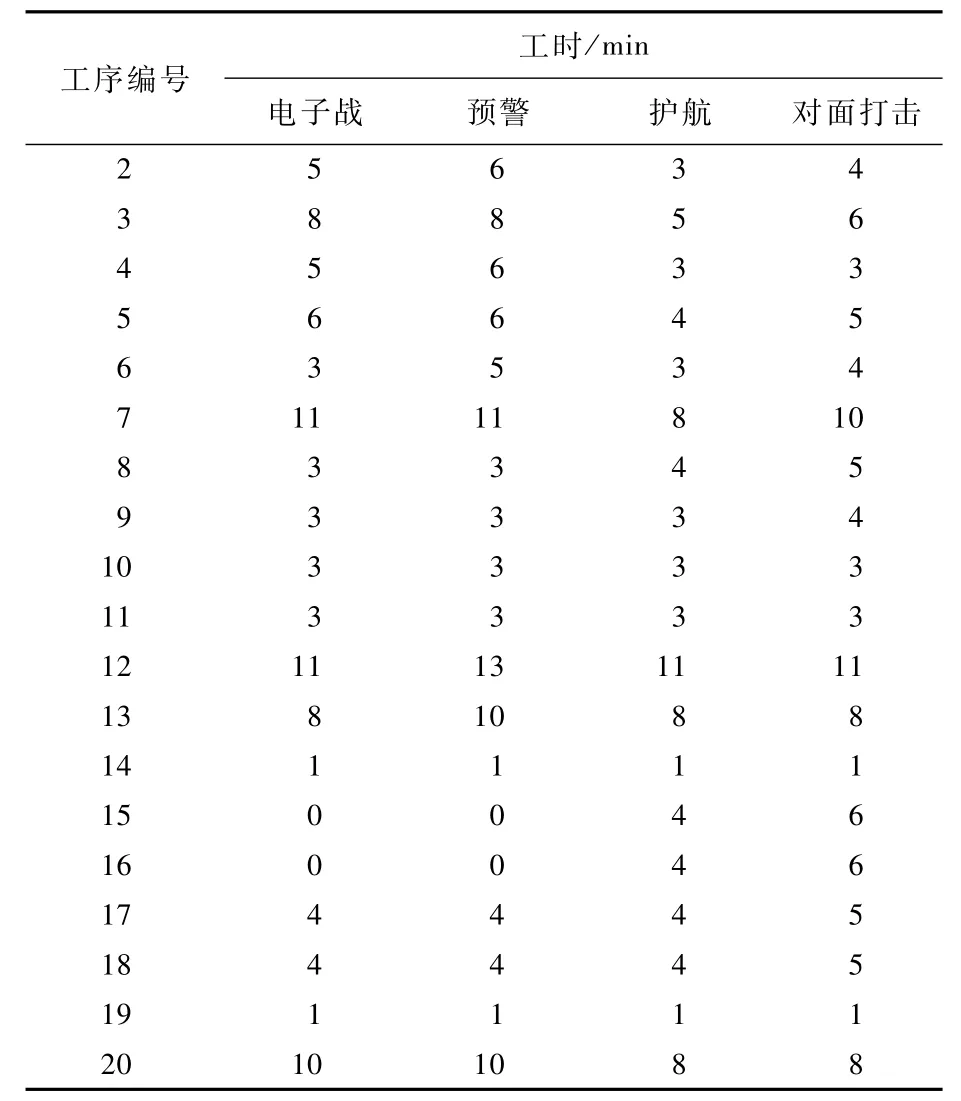
表2 各出動任務(wù)下保障工序工時Table 2 Support operation durations of different sortie missions
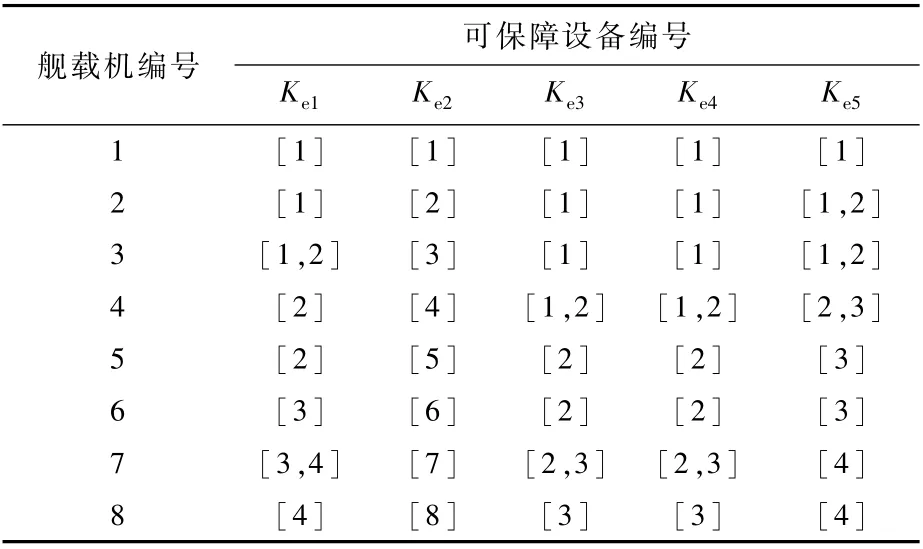
表3 保障設(shè)備與艦載機保障覆蓋關(guān)系Table 3 Reachability r elation between carrier-based aircr aft and support equipments
經(jīng)過多次實驗對比擇優(yōu),雙向人工蜂群算法參數(shù)選取為:蜜源數(shù)目NS=30,蜜源停留最大限制搜索次數(shù)NL=15,迭代終止條件設(shè)置為調(diào)度最大評價次數(shù)6 000。為克服調(diào)度優(yōu)化的隨機性,對每個保障人員配置方案進行n次調(diào)度優(yōu)化,并取其目標值均值作為輸出,本文設(shè)置n=5。
4.2 運算結(jié)果分析
基于MATLAB 2017編程運算,可得基于邊際-人工蜂群算法求解艦載機機群出動保障人員配置-調(diào)度聯(lián)合優(yōu)化的目標值收斂曲線如圖5和圖6所示。其中,機群出動保障完工時間呈現(xiàn)單調(diào)遞減趨勢,最終收斂至Cmax=53.5 min;而保障人員負載方差和則為波動趨勢,最終輸出結(jié)果為L=25.2。在外層迭代過程中,以機群出動保障完工時間作為第一優(yōu)先目標,因此每次迭代所選擇專業(yè)增加保障人員雖然能確保縮短保障完工時間,然而可能會對該專業(yè)保障均衡性帶來不確定的影響,而隨著人員數(shù)量的增加,該波動趨緩。
最終優(yōu)化所得人員配置方案為[4,4,8,9],迭代過程如圖7所示。由于機械專業(yè)和軍械專業(yè)的保障任務(wù)相對繁重,所需保障人員明顯多于特設(shè)專業(yè)和航電專業(yè)的保障人員,這也與實際保障狀況相吻合。
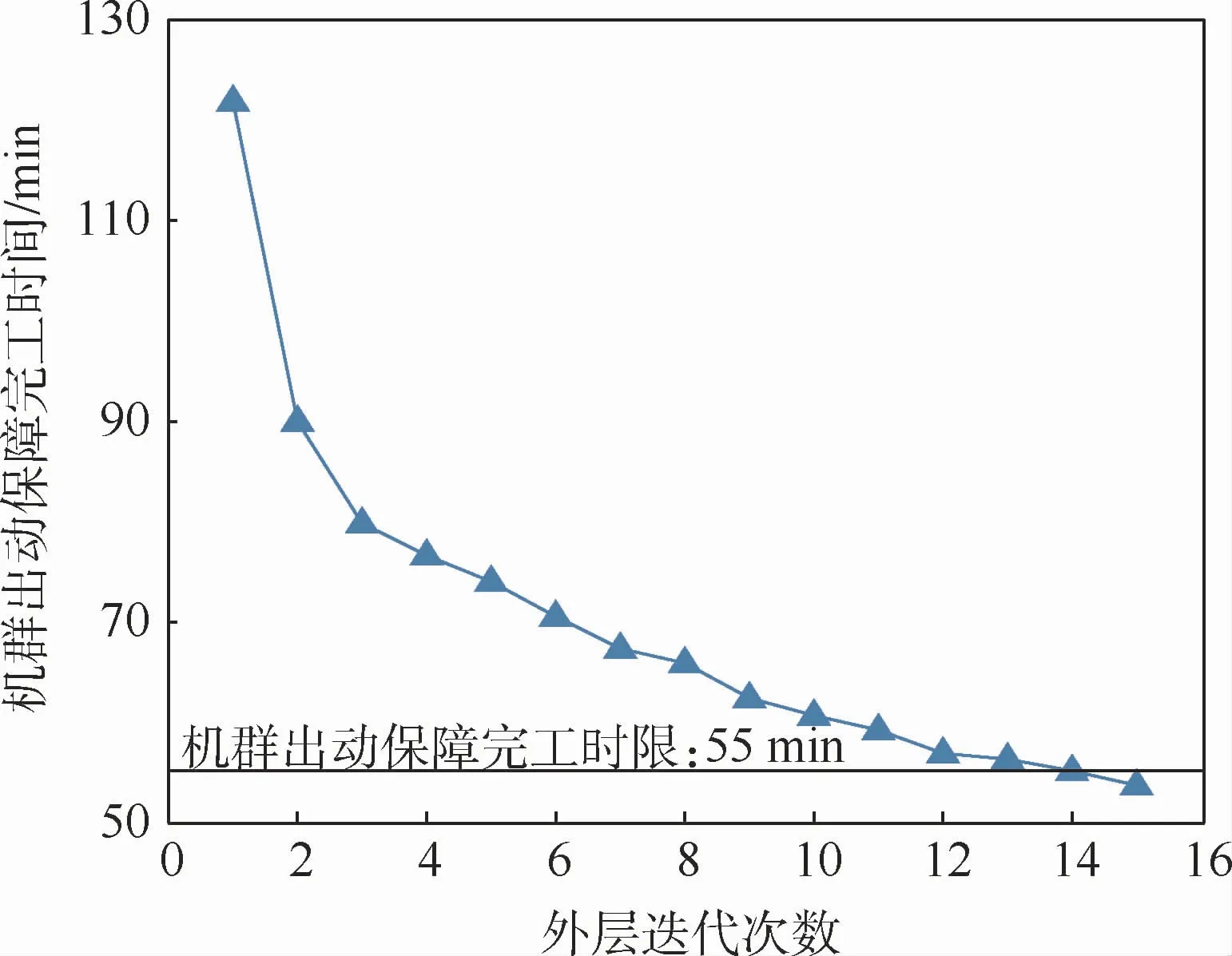
圖5 機群出動保障完工時間隨外層迭代次數(shù)收斂Fig.5 Convergence curve of aircraft fleet sortie support completion time with the increase of external iterations times
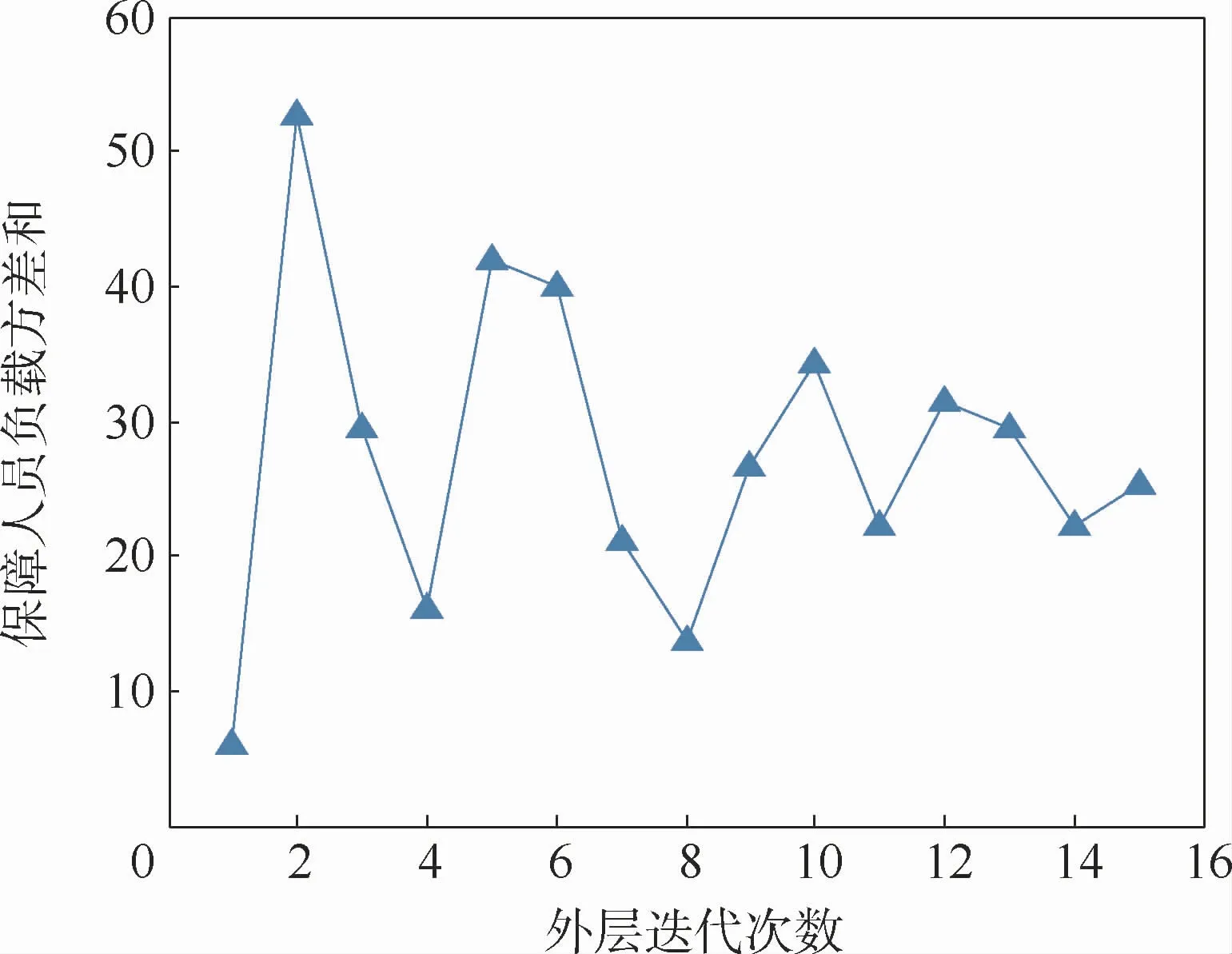
圖6 保障人員負載方差和隨外層迭代次數(shù)變化Fig.6 Variation trend of support personnel load variance sum with the increase of external iterations times
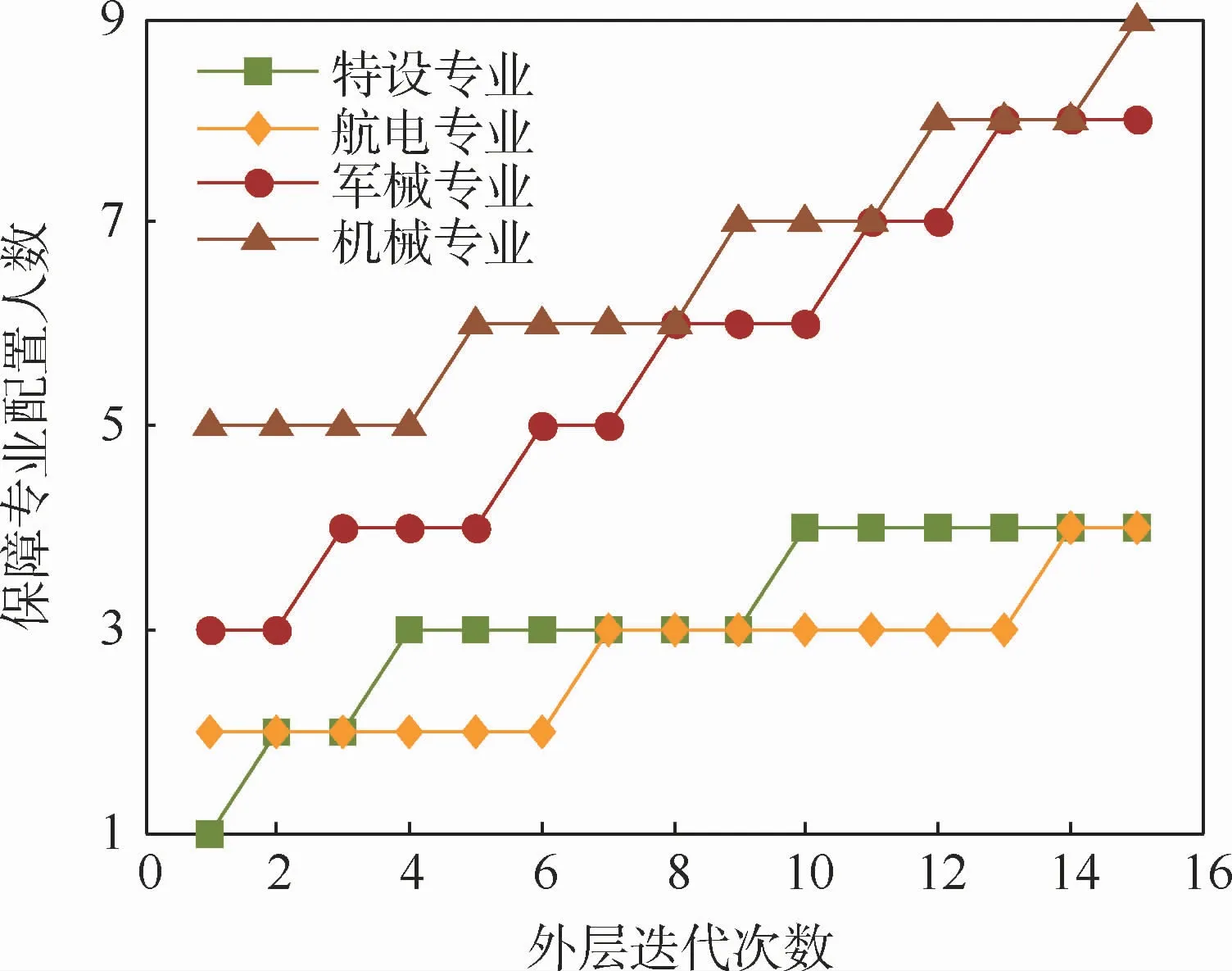
圖7 保障人員配置迭代過程Fig.7 Iteration trends of support personnel configuration
相對于固定機組制的保障模式,一體化聯(lián)合保障模式下對保障人員的需求明顯減少,在固定機組制下一般配置各專業(yè)保障人員共8人,本文保障模式下可減少需求39人。此外,為確定本文所提出初始配置模型的魯棒性,進一步選取特設(shè)專業(yè)的人數(shù)為2和3,分別在這2種配置強度下確定初始保障人員配置,通過邊際-人工蜂群優(yōu)化算法所得結(jié)果均與本次結(jié)果相同,最終配置方案均為[4,4,8,9],因此該初始配置方法在一定范圍內(nèi)具備尋優(yōu)的魯棒性,且可顯著減少迭代次數(shù),提升優(yōu)化效率。


圖8 保障人員調(diào)度甘特圖Fig.8 Gantt chart of support personnel scheduling
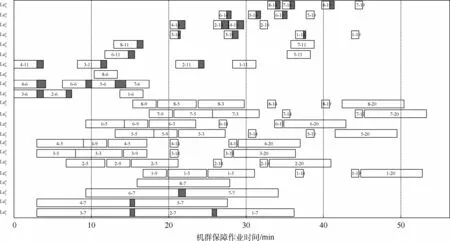
圖9 保障設(shè)備調(diào)度甘特圖Fig.9 Gantt chart of support equipment scheduling

4.3 算法分析

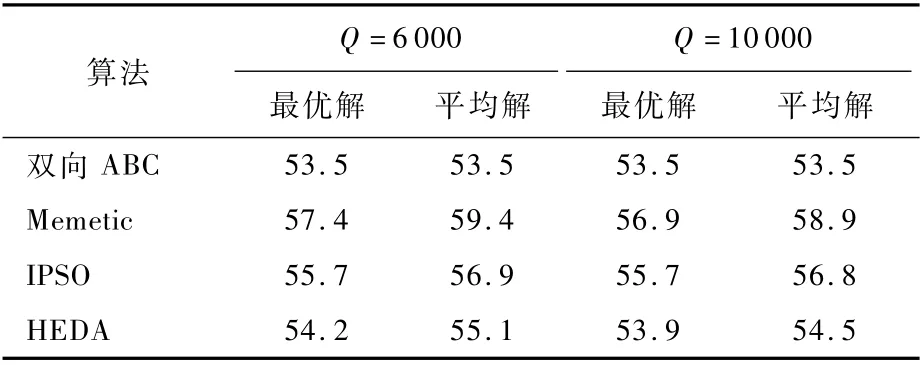
表4 算法對比結(jié)果Table 4 Comparison of different algorithms min
5 結(jié)束語
本文針對艦載機機群出動保障人員配置及調(diào)度聯(lián)合優(yōu)化問題,系統(tǒng)分析了保障過程的流程、資源工位轉(zhuǎn)移和出動時限約束情況,構(gòu)建了相應(yīng)的數(shù)學模型;提出了基于邊際-人工蜂群算法的兩層優(yōu)化決策架構(gòu),其中上層決策模型基于邊際優(yōu)化算法對保障人員配置方案進行迭代改進,下層決策模型基于改進的雙向人工蜂群算法,結(jié)合上層確定的人員配置方案,對艦載機機群出動保障任務(wù)進行調(diào)度優(yōu)化。針對上層保障人員配置,提出了基于人員配置強度的初始配置方法以縮短迭代次數(shù);針對下層調(diào)度優(yōu)化,引入差分進化的交叉變異策略及面向種群的雙向?qū)R機制。典型出動保障案例仿真結(jié)果表明,所提出的邊際-人工蜂群兩層優(yōu)化算法可有效解決艦載機機群出動保障人員配置及調(diào)度聯(lián)合優(yōu)化問題,且無論是上層的保障人員初始配置方法,還是下層的保障調(diào)度優(yōu)化算法,針對優(yōu)化結(jié)果均具有較強的魯棒性,所生成的保障資源分配方案和時序方案可滿足模型的各項約束,為甲板保障作業(yè)資源配置和調(diào)度提供一套新的聯(lián)合決策方法,對提升艦載機機群甲板作業(yè)的保障效率和資源利用率,促進航空保障“減員增效”均具有一定理論指導意義和工程應(yīng)用價值。結(jié)合甲板作業(yè)的不確定性,拓展保障資源的決策優(yōu)化范圍,開展不確定環(huán)境下艦載機保障的前攝-反應(yīng)式資源配置及動態(tài)調(diào)度研究是下一步的研究方向。

