ON THE NUCLEARITY OF COMPLETELY 1-SUMMING MAPPING SPACES*
Zhe DONG (董 浙)
School of Mathematical Sciences, Zhejiang University, Hangzhou 310027, China E-mail : dongzhe@zju.edu.cn Yafei ZHAO (趙亞菲)
Department of Mathematics, Zhejiang International Studies University, Hangzhou 310012, China E-mail : zhaoyafei zju@163.com



For the ordinary systems of mapping spaces,we can give the following definition:
Definition 1.3An operator spaceVis nuclear(in the system)if there exists the following diagram of complete contractions which approximately commute in the point-norm topology:
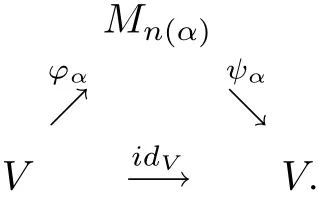
As we know,mapping spaces provide a fundamental tool for studying Banach spaces and operator spaces.In this note,we are interested primarily in the nuclearity in the system of completely 1-summing mapping spaces(Π1(·,·),π1).To our surprise,we obtain that C is the unique operator space which is nuclear in the system(Π1(·,·),π1).
2 Nuclearity in(Π1(·,·),π1)
Definition 2.1An operator spaceVis nuclear in the system of completely 1-summing mapping spaces(Π1(·,·),π1)if there exists the following diagram of linear mappings withπ1(?α)≤1,π1(ψα)≤1 which approximately commute in the point-norm topology:
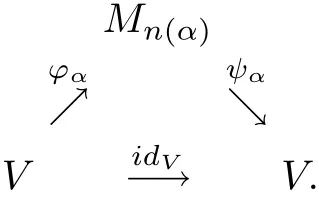
Lemma 2.2An operator spaceVis nuclear in the system of(Π1(·,·),π1)if and only ifVis nuclear andπ1(idV)≤1.
ProofSuppose thatVis nuclear in the system of(Π1(·,·),π1);it is clear thatVis nuclear.From Definition 2.1,there exists the following diagram of linear mappings withπ1(?α)≤1,π1(ψα)≤1,which approximately commute in the point-norm topology:

Corollary 13.4.2 in[5]implies thatν(ψα??α)≤π1(ψα)·π1(?α)≤1.Since the netψα??αconverges toidVin the point-norm topology,it follows from Lemma 12.3.1 in[5]thatι(idV)≤1.Thusπ1(idV)≤ι(idV)≤1.
Conversely,suppose thatVis nuclear andπ1(idV)≤1.By the nuclearity ofV,there exists the following diagram of complete contractions which approximately commute in the point-norm topology:
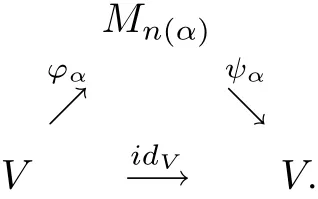

Theorem 2.4An operator spaceVis nuclear in the system of completely 1-summing mapping spaces(Π1(·,·),π1)if and only ifV=C.
ProofIt is clear,by the definition ofπ1in Section 1,thatπ1(idC)=1.Thus it follows from Definition 2.1 that C is nuclear in the system of(Π1(·,·),π1).
To prove the necessity of this,we suppose thatVis nuclear in the system of completely 1-summing mapping spaces(Π1(·,·),π1).From Definition 2.1,there exists the following diagram of linear mappings withπ1(?α)≤1,π1(ψα)≤1 which approximately commute in the pointnorm topology:
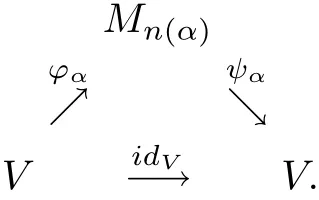
It follows from Lemma 2.2 thatπ1(idV)≤1.By Corollary 13.4.2 in[5]we have
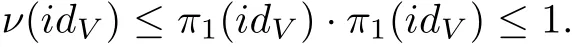
ThusidVis completely nuclear.Proposition 12.2.1 in[5]shows thatidVis compact in the Banach space sense,and from classical theory,Vmust be finite dimensional,and soV=V??.By Lemma 2.2 and Theorem 14.6.7 in[5],V=V??is injective.Thus,by Corollary 6.1.8 in[5]we have


Sinceiis a complete isometry andPis a complete quotient mapping,i?is a complete quotient mapping andP?is a complete isometry.Thus it follows from(7.1.27)and Proposition 8.1.5 in[5]that the following embeddings are complete isometries:


3λ-Nuclearity in(Π1(·,·),π1)
Definition 3.1An operator spaceVisλ-nuclear in the system of completely 1-summing mapping spaces(Π1(·,·),π1)if there exists the following diagram of complete contractions withπ1(?α)≤λ,π1(ψα)≤λ,which approximately commute in the point-norm topology:

It is clear from Definition 2.1 and Definition 3.1 that nuclearity in(Π1(·,·),π1)is equivalent to 1-nuclearity in(Π1(·,·),π1).
Lemma 3.2An operator spaceVisλ-nuclear in the system of(Π1(·,·),π1)if and only ifVis nuclear andπ1(idV)≤λ.
ProofThe proof is similar to that of Lemma 2.2.Suppose thatVisλ-nuclear in the system of(Π1(·,·),π1);it follows from Definition 3.1 and Definition 1.3 thatVis nuclear and that there exists the following diagram of complete contractions withπ1(?α)≤λ,π1(ψα)≤λ,which approximately commute in the point-norm topology:
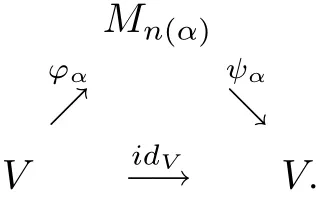
Thus we haveν(ψα??α)≤π1(ψα??α)≤‖ψα‖cb·π1(?α)≤λ.Since the netψα??αconverges toidVin the point-norm topology,it follows from Lemma 12.3.1 in[5]thatι(idV)≤λ.Thusπ1(idV)≤ι(idV)≤λ.
Conversely,suppose thatVis nuclear andπ1(idV)≤λ.By nuclearity ofV,there exists the following diagram of complete contractions which approximately commute in the point-norm topology:
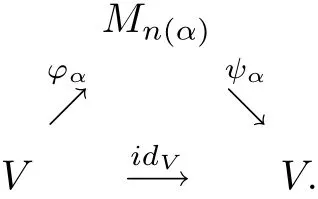


 Acta Mathematica Scientia(English Series)2020年6期
Acta Mathematica Scientia(English Series)2020年6期
- Acta Mathematica Scientia(English Series)的其它文章
- IT?O DIFFERENTIAL REPRESENTATION OF SINGULAR STOCHASTIC VOLTERRA INTEGRAL EQUATIONS?
- EXISTENCE AND UNIQUENESS OF THE POSITIVE STEADY STATE SOLUTION FOR A LTKA-VTE PEDPY MD WIH CING*
- ASYMPTOTICS OF THE CROSS-VARIATION OF YOUNG INTEGRALS WITH RESPECT TO A GENERAL SELF-SIMILAR GAUSSIAN PROCESS?
- THE DECAY ESTIMATES FOR MAGNETOHYDRODYNAMIC EQUATIONS WITH COULOMB FORCE*
- VAR AND CTE BASED OPTIMAL REINSURANCE FROM A REINSURER'S PERSPECTIVE*
- ON THE COMPLETE 2-DIMENSIONAL λ-TRANSLATORS WITH A SECOND FUNDAMENTAL FORM OF CONSTANT LENGTH*
