EXISTENCE AND UNIQUENESS OF THE POSITIVE STEADY STATE SOLUTION FOR A LTKA-VTE PEDPY MD WIH CING*
?Xianzhong ZENG (曾憲忠)? Lingyu LIU (劉玲妤) Weiyuan XIE (謝偉圓)
School of Mathematics and Computing Science, Hunan University of Science and Technology,Xiangtan 411201, China E-mail : zxzh217@sohu.com; 591283884@qq.com; 2310945546@qq.com


In this paper,we study the following Lotka-Volterra predator-prey model with a crowding term in the predator equation:

This paper is organized as follows:in Section 2,we give some preliminaries;in Section 3,by employing the local and global bifurcation theories[6,8–10,21,33,43],we obtain the existence and the global structure of the positive steady state solutions of(1.3);in Section 4,by using the Lyapunov-Schmidt reduction,we obtain the fine profile of the uniqueness of the positive steady state solution of(1.3);in Section 5,we show that whenμ≥λD1(?0),the predator does not exist in?0and the prey is equal to zero in?0.
2 Preliminaries

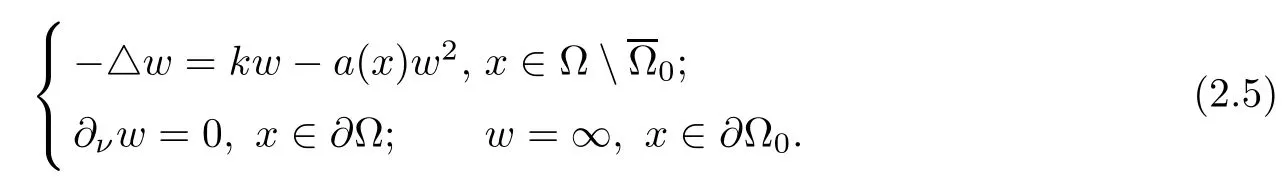
As far as we know,Problems(2.3),(2.4)and(2.5)have been widely studied.Here,we mainly quote some results of[16,17,22,26,31].The readers can look at[3–5,16–18,22,25,26,31]and references therein for more research results.Now,we collect the results of the equations(2.3)–(2.5)in the Lemmas 2.1–2.3,where Part(ii)of Lemma 2.1 quotes a research result obtained by Professor Lopez-Gomez(see[22]or Theorem 6.1 of[26]),and other parts of Lemmas 2.1–2.3 quote some research results obtained by Professors Du and Huang[16,17],and Ouyang[31].In addition,it should be noted that Lemma 2.4 was obtained in[39].

3 Existence of the Positive Solutions of(2.2)
In this section,by employing the local and global bifurcation theories[6,8–10,21,33],we will obtain the existence of the positive solutions of(2.2).
3.1 Local bifurcation analysis


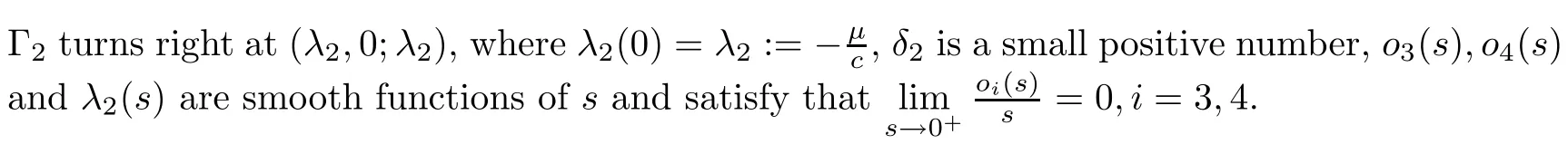
(iii)By a similar argument,(2.2)has no positive solution emanating from any point on Γ0for any fixedμ≠0.As forμ=0,by using the Lyapunov-Schmit reduction in Section 4 below,we obtain that the curve of the positive solutions of(2.2)may emanate from the point(0,0;λ)=(0,0;0).
By the arguments above,we obtain the following results:
Lemma 3.1Suppose thatμ,bandcare fixed.Then the following results hold:

3.2 Global bifurcation analysis



4 Uniqueness of the Positive Solution of(2.2)
In this section,we investigate the uniqueness of the positive solution of(2.2).Although we may obtain the uniqueness of the positive solution of(2.2)whenborcare near to zero by using the perturbation theory of the linearized operator,this result is not fine.In what follows,by using the Lyapunov-Schmit reduction,we will obtain the fine profile of the uniqueness of the positive solution of(2.2).One can look at[34,35,42]and references therein for discussion of some models using the Lyapunov-Schmidt reduction.
4.1 Lyapunov-Schmidt Reduction

whereX1andY1are theL2-orthogonal spaces ofR2inXandY,respectively.LetP:X→X1andQ:Y→Y1be the orthogonal projections.Then every solution(w,z)of(4.2)may be uniquely decomposed as
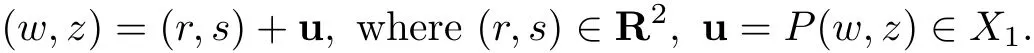

4.2 Structure of the solutions ofΦ0((r,s);α)=0

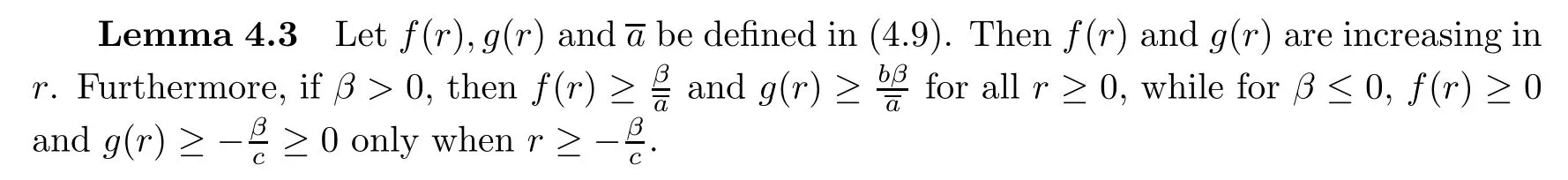
4.3 Construction of the positive solutions of(4.1)
In this subsection,by perturbing the solutions curve{((r,f(r));g(r))}ofΦ0((r,s);β)=0,we will construct the positive solutions of(4.1)forε>0 small enough,which yields a fine profile of the curve of the positive solutions of(2.2).In what follows,we only discuss the caseβ>0;as the caseβ≤0 is similar,we omit it.

Furthermore,by perturbing the set{((r,f(r));g(r)):0≤r≤C1},we may obtain the following proposition:
Proposition 4.4Assume thatβ>0 is fixed.LetC1andA1be defined in(4.10).Then there existε0>0 and a family of bounded smooth curves






5 Nonexistence of the Positive Solution of(2.2)


 Acta Mathematica Scientia(English Series)2020年6期
Acta Mathematica Scientia(English Series)2020年6期
- Acta Mathematica Scientia(English Series)的其它文章
- IT?O DIFFERENTIAL REPRESENTATION OF SINGULAR STOCHASTIC VOLTERRA INTEGRAL EQUATIONS?
- ON THE NUCLEARITY OF COMPLETELY 1-SUMMING MAPPING SPACES*
- ASYMPTOTICS OF THE CROSS-VARIATION OF YOUNG INTEGRALS WITH RESPECT TO A GENERAL SELF-SIMILAR GAUSSIAN PROCESS?
- THE DECAY ESTIMATES FOR MAGNETOHYDRODYNAMIC EQUATIONS WITH COULOMB FORCE*
- VAR AND CTE BASED OPTIMAL REINSURANCE FROM A REINSURER'S PERSPECTIVE*
- ON THE COMPLETE 2-DIMENSIONAL λ-TRANSLATORS WITH A SECOND FUNDAMENTAL FORM OF CONSTANT LENGTH*
