變質心技術發展與應用

周敏 周鳳岐 周軍 郭建國

摘 要：變質心技術利用飛行器內部質量塊移動改變質心位置， 無氣動舵、 直接力等傳統控制方式熱燒蝕、 舵面顫振、 燃料消耗問題， 控制效率高， 有利于保持機體良好氣動外形。 本文基于變質心控制內涵， 分類總結了變質心實現與配置的兩種形式及其特點， 詳細梳理了滾轉控制、 配平控制和復合控制三種變質心控制模式的研究進展。 最后， 通過分析變質心技術面臨的復雜多體動力學建模、 強耦合強非線性控制、 高動態高性能執行機構設計與研制等關鍵難點問題， 展望變質心技術應用新場景， 為未來變質心技術研究指明了方向。

關鍵詞： ????變質心; 總體配置; 滾轉控制; 配平控制; 復合控制; 飛行器控制

中圖分類號：???? TJ765; V249.1? 文獻標識碼：??? A 文章編號：???? 1673-5048（2021）06-0007-07

0 引? 言

變質心是指通過主動改變飛行器質心位置， 產生期望控制效應的一種新概念控制技術。 該技術最早是由美俄科學家提出并發展起來的。 而美國的變質心技術研究起步最早、 最成熟。 1975年， 美國完成了機動彈頭MK-500的飛行試驗， 該彈頭就采用了變質心技術， 通過移動彈頭內部電子裝置實現彈頭質心位置變化[1]， 但其他研究細節一直處于高度保密狀態， 直到1996年， 公開文獻中才首次出現與MK-500機動彈頭的變質心應用方案相近的研究內容[2]。

俄羅斯的變質心技術發展十分迅速， 目前也已實現工程應用。 作為首個能夠完全在俄羅斯本國境內研制和生產的戰略彈道導彈， 白楊-M就采用了變質心技術。 從1993年進入工程研制， 到1997年完成飛行試驗， 白楊-M用時不到5年就進入了俄羅斯戰略核力量作戰序列， 成為其核威懾力量的中流砥柱[3]。

從美俄的變質心技術應用現狀和相關技術細節的保密程度不難窺見， 變質心技術研究對于提升機動彈頭、 彈道導彈等武器性能具有重要意義。 鑒于此， 西北工業大學周鳳岐教授于1993年在國內最早提出并開展變質心技術研究， 其團隊針對變質心飛行器總體、 制導控制、 仿真試驗以及伺服機構等方面內容開展了系統性的深入研究[4-9]， 引領并推動了國內變質心技術從概念研究到工程應用的全過程。 另外， 哈爾濱工業大學、 北京理工大學等單位的學者也對該技術進行了深入研究[10-12]。

本文在闡述變質心控制內涵的基礎上， 對變質心實現與配置形式進行了分類介紹， 總結了變質心技術應用于飛行器姿態控制的三種模式及其研究現狀， 對未來變質心技術發展面臨的關鍵難點問題和主要應用場景進行了展望。

1 變質心控制內涵

飛行器變質心最直接的效應是改變系統質量分布， 由此導致系統質心位置變化和慣性主軸偏移。 基于此， 變質心技術可用于實現三種不同的控制效應， 分別是用于主動調節飛行器質心和壓心距離， 調控系統操控性能; 用于主動改變飛行器慣量特性， 控制飛行器的角運動規律; 用于調節飛行器所受合外力的作用力臂大小， 產生可變力矩作用實現姿態控制。 其中， 變質心姿態控制效應利用飛行器質量特性主動變化所產生的控制力矩， 因此也被稱為質量矩控制。

相比于常見的氣動舵、 擺動噴管、 直接力等飛行器姿態控制手段， 變質心姿態控制有其優越性：

（1） 不存在氣動舵面、 直接力噴管等外露執行機構的熱燒蝕問題;

（2） 不存在直接力噴流干擾、 氣動舵面顫振等不確定干擾作用;

（3） 變質心機構完全置于飛行器內部， 有利于保持飛行器良好氣動外形， 獲得更好的氣動特性;

（4） 利用整個飛行器機體為控制作動面， 費效比低， 控制效率高。

2 變質心實現與配置

變質心控制按照控制的姿態運動通道數可分為一維變質心控制、 二維變質心控制和三維變質心控制。 一維變質心控制實現飛行器俯仰、 偏航、 滾轉任一通道的姿態控制; 二維變質心控制實現俯仰、 偏航、 滾轉三通道中任意兩個通道的姿態控制; 三維變質心控制則需要完成飛行器全部三通道姿態控制。 一維/二維/三維變質心控制實現以變質心機構配置為基礎， 依賴于飛行器內部可動質量塊的安裝與運動方式， 可分為兩類： 變質心直角坐標配置和變質心極坐標配置。

2.1 變質心直角坐標配置

周 敏， 等： 變質心技術發展與應用

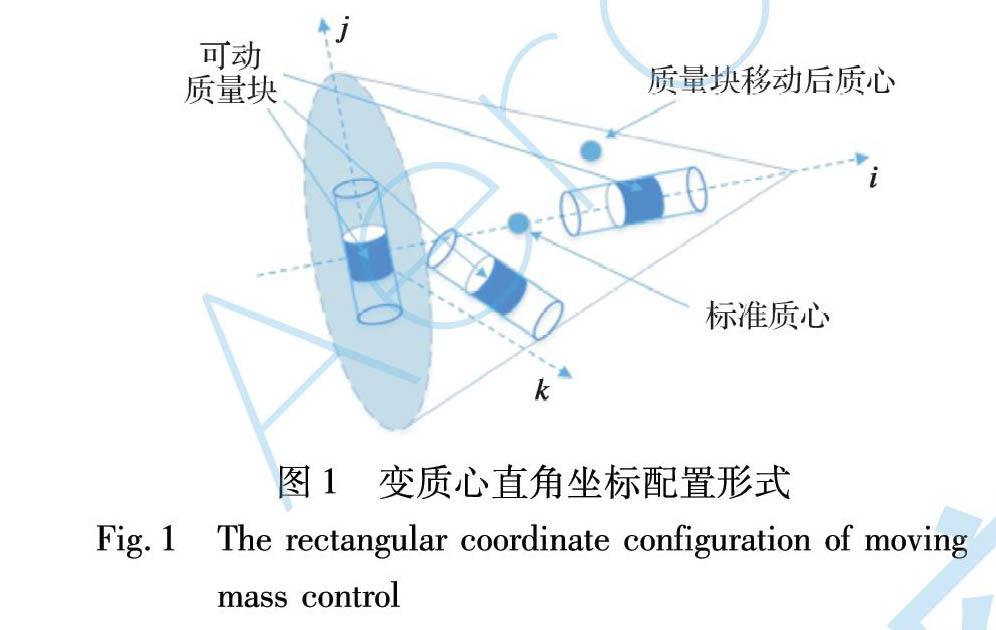
變質心直角坐標配置， 顧名思義就是在直角坐標系框架內實現飛行器質心變化的配置方式。 圖1為一種典型的變質心直角坐標配置： 三個可動質量塊分別在三個直線導軌上移動， 三個直線導軌相互垂直且分別與飛行器本體坐標系的三個坐標軸平行。 此時， 三個質量塊移動能夠實現飛行器系統總質心在本體坐標系三個軸向的位置分量。

定義可動質量塊均處于位移零位時的系統總質心位置為系統質心零位; 記飛行器本體坐標系三個坐標軸的單位矢量分別為i， j， k。 當變質心機構作用即可動質量塊移動時， 記系統瞬時質心相對于系統質心零位的位置矢量為r1=x1i+y1 j+z1k， 假設此時飛行器受到的合外力矢量為F=Fxi+Fy j+Fzk， 合外力作用點相對于系統質心零位的位置矢量為r2=x2i+y2 j+z2k。 此時， 變質心機構作用下飛行器所受合外力矩變化量為

MC=（r2-r1）×F=（yFz-zFy）i+（zFx-xFz）j+（xFy-yFx）k （1）

其中：

x=x2-x1; y=y2-y1; z=z2-z1。

顯然， 三個可動質量塊的獨立運動能夠改變飛行器滾轉、 偏航、 俯仰通道所受外力矩大小， 實現三通道姿態控制; 但各通道所受力矩分量由兩個方向的可動質量塊運動共同決定， 即飛行器三通道姿態控制存在通道間交叉耦合特性。

以滾轉通道的力矩分量（yFz-zFy）為例。 當飛行器受側向力Fz、 法向力Fy作用時， 沿j向和k向的質心位置變化量y和z將共同決定飛行器受到的滾轉力矩大小， j向質心位置變化量y同時也影響俯仰力矩大小， 飛行器的滾轉姿態運動與俯仰姿態運動耦合; 同理， 考慮k向質心位置變化量z影響時， 滾轉姿態運動與偏航姿態運動耦合; 考慮i向質心位置變化量x影響時， 偏航姿態運動與俯仰姿態運動耦合。

如果飛行器采用BTT （Bank-To-Turn）飛行模式， 其理想飛行狀態下的側向運動為零， 受到的側向力分量近似滿足Fz≈0， 此時式（1）簡化為

MC=-zFyi+zFx j+（xFy-yFx）k（2）

顯然， 變質心控制下的BTT飛行器受到的滾轉力矩和偏航力矩均由系統k向質心位置變化量決定。 可見， 變質心控制應用于BTT飛行器時存在欠驅動特性， 可以通過設計合理的通道間協同策略確定k向移動質量塊運動， 實現滾轉姿態控制和偏航姿態穩定; 也可以通過引入其他控制手段與變質心復合， 實現飛行器的三通道姿態控制。 如給BTT飛行器配置方向舵實現偏航穩定， k向移動質量塊在較大法向力作用下具有較強滾轉姿態控制能力， 沿i向和j向移動的可動質量塊則共同完成俯仰通道的姿態控制。 可見， 三個可動質量塊的變質心機構不一定用于實現飛行器三通道姿態控制， 即如圖1所示的直角坐標變質心機構不一定是三維變質心機構。

需要特別說明的是： 變質心直角坐標配置中， 質量塊相對于飛行器本體只有平動而無轉動運動。

2.2 變質心極坐標配置

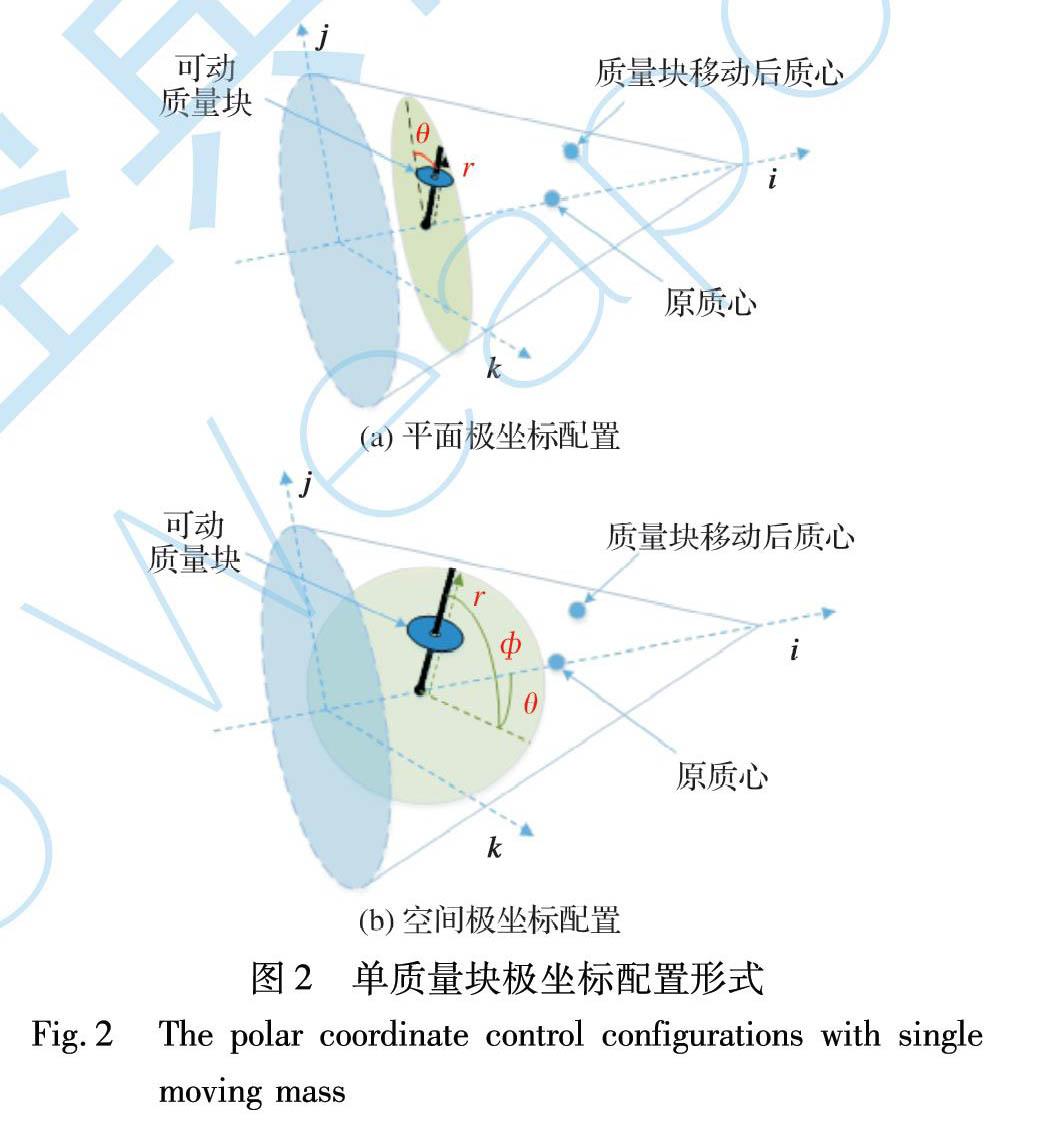
變質心極坐標配置， 顧名思義就是在極坐標系框架內實現飛行器質心變化的配置方式。 在此， 給出兩種典型的變質心極坐標配置， 如圖2所示。

變質心平面極坐標配置就是在平面極坐標框架內實現系統質心變化的可動質量塊配置形式。 如圖2（a）所示， 單質量塊沿直線導軌運動， 通過將直線導軌一端與飛行器本體鉸接， 實現直線導軌在以飛行器本體坐標系i軸為法向量的平面內轉動。 在該配置中， 通過改變質量塊相對于鉸接點的徑向距離r和直線導軌旋轉位置象限角θ， 即改變兩個自由變量組合（r，θ）， 實現飛行器系統質心在i平面內變化， 即j向和k向兩個方向上的主動變化。

若將圖2（a）極坐標配置中導軌的平面鉸接更換為球形鉸接， 就可以得到如圖2（b）所示的單質量塊空間極坐標配置。 在該配置中， 通過改變可動質量塊相對于鉸接點的距離以及直線導軌在三維空間中的指向角度θ和， 即改變三個自由變量組合（r， θ， ）， 可實現飛行器系統質心在三維空間中的主動變化。

若將圖2中的導軌+滑塊配置替換為雙滑塊， 也可以實現如圖3所示的變質心平面極坐標配置： 兩個質量塊能夠沿著以飛行器本體坐標系i軸為法向量的圓環形導軌運動。 在該配置中， 通過改變兩個質量塊的位置象限角θ1和θ2大小， 即改變兩個自由變量組合（θ1，θ2）， 實現飛行器系統質心在i平面內變化， 即j向和k向兩個方向上的主動變化。 在此基礎上， 若圖3所示平面極坐標配置中的環形導軌還能夠在i向前后移動， 就可以進一步實現飛行器系統質心在三維空間中的主動變化。 與直角坐標配置相比， 實現變質心極坐標配置的可動質量塊運動更加復雜， 相對于飛行器本體做平動與轉動運動的疊加。 因此， 極坐標配置下的變質心飛行器動力學更加復雜。

配置可動質量塊以實現變質心控制并沒有固定形式， 而是需要綜合飛行器總體布局約束、 飛行控制需求和工程應用實際限制等多方面因素進行取舍和平衡， 完成優化設計。 總結變質心直角坐標配置和極坐標配置區別如表1所示。

3 變質心控制模式

變質心技術應用于飛行器姿態控制時主要實現變質心滾轉控制MMRC （Moving Mass Roll Control）、 變質心配平控制MMTC （Moving? Mass? Trim? Control）和變質心復合控制MMPC （Moving Mass Compound Control）三種模式。

3.1 滾轉控制

變質心滾轉控制（MMRC）是指利用變質心技術實現飛行器滾轉姿態控制， 是較早深入研究并成功工程化的一種變質心技術應用模式。 變質心滾轉控制最典型的應用對象是固定配平型飛行器（Fixed-trim vehicle）， 此類飛行器利用上下非對稱氣動布局或非對稱質量分布特性獲得確定的非零配平攻角。 圖4所示為采用彎頭錐氣動布局和截錐氣動布局兩種方式， 實現飛行器上下非對稱氣動布局的固定配平型飛行器總體外形。 美國海軍研制的MK-500逃逸型機動彈頭就是采用了彎頭錐外形的固定配平型飛行器， 依賴確定的非零配平攻角產生一定升力， 再以彈頭內部電子裝置作為可動質量塊實現彈頭滾轉姿態控制[11]。

固定配平型飛行器執行機構少、 結構簡單， 但配平攻角大小由氣動布局設計提前確定， 變質心也只實現滾轉控制， 存在過載大小不可控僅方向可控的特點， 導致其軌跡規劃與制導實現存在困難[13-14]， 為此， 相關學者經過多年研究提出了多種解決方法。

固定配平型飛行器基于單質量塊的滾轉控制存在著多剛體復雜動力學建模、 強耦合強魯棒控制等問題。 美國海軍水面作戰中心和馬里蘭大學的研究人員最先開展相關工作， 建立了單質量塊飛行器二體七自由度數學模型， 采用現代控制理論的線性最優控制方法設計了滾轉自動駕駛儀。 文獻[15-16]分別從時域、 頻域分析了變質心滾轉控制的固定配平型飛行器動力學特性， 研究了變質心滾轉控制機理。 文獻[17]基于拉格朗日方法建立了單質量塊變質心固定配平型飛行器的多剛體動力學模型， 然后采用軌跡線性化方法設計了滾轉控制系統， 具有較強的魯棒性。 劉智陶[18]基于自抗擾控制方法設計了滾轉/偏航耦合欠驅動控制器， 利用單個可動質量塊同時實現滾轉角跟蹤和側滑角鎮定， 充分利用了單質量塊變質心的控制能力。

3.2 配平控制

變質心配平控制（MMTC）主要用于實現飛行器俯仰通道攻角配平和偏航通道側滑角配平控制， 是最直接的變質心技術應用模式。 美國海軍系統作戰中心的Regan等[19]早在1984年就對變質心配平控制進行了研究， 用于修正彈道式再入飛行器航程以提高目標點精度。 隨后， 研究人員分別針對快速旋轉彈道式軸對稱飛行器和慢速旋轉再入飛行器開展了變質心配平控制機理研究[20-21]， 明確了快速旋轉飛行器配平攻角主要由慣性主軸偏移產生， 慢速旋轉飛行器配平攻角則依賴于質心偏移和氣動阻力的綜合作用， 且較小穩定裕度是慢速旋轉飛行器實現變質心較大配平控制能力的前提。

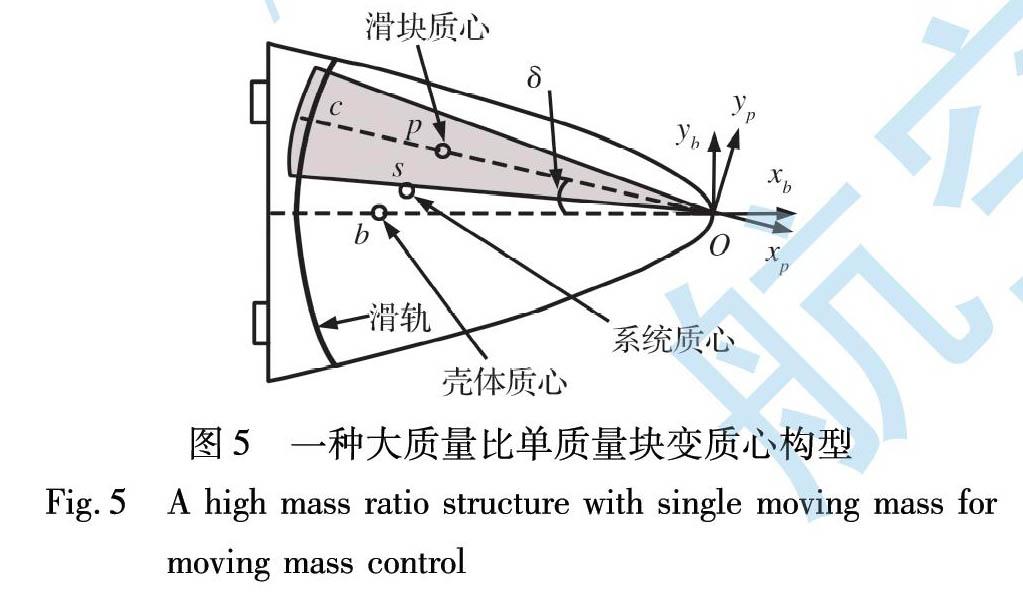
變質心配平控制通常需要配置多個可動質量塊， 文獻[22]配置三個可動質量塊用于完成動能彈頭俯仰通道和偏航通道的配平控制， 但多質量塊配置必然給飛行器總體布局帶來很大壓力， 導致基于多質量塊的變質心配平控制的工程應用難度很大。 因此， 采用較少質量塊實現變質心控制越來越受到研究人員的重視。 如Chen等[23]利用兩個可動質量塊直角坐標配置， 實現了面對稱再入飛行器的俯仰配平控制和滾轉控制， 設計了考慮質量塊移動行程受限的增益自適應控制方法， 結果表明兩個質量塊的變質心控制具有較好的動態響應。 Gao等[24]利用單個可動質量塊的極坐標配置實現了變質心配平控制， 采用兩質量塊直角配置或單質量塊極坐標配置都能有效減少可動質量塊數量， 降低變質心配置對飛行器總體布局的壓力。 此外， 李澗青等[25]提出了圖5所示的單質量塊變質心配置方案， 使可動質量比達到60%以上， 同時保證了質量塊配置數量少、 配平控制能力強兩方面需求， 但該配置方案的工程可實現性和可靠性還有待深入研究與驗證。

3.3 復合控制

隨著飛行任務的不斷復雜化， 大空域、 高精度、 強機動成為飛行控制的重要需求。 但是， 變質心控制性能受制于飛行器外力作用特性， 如稀薄大氣條件下氣動力不可用、 稠密大氣條件下直接力噴流擾動嚴重等， 這都導致變質心技術應用場景受限、 控制性能降低。 另一方面， 可動質量塊配置受到飛行器內部空間限制和總體布局約束， 且變質心滾轉控制（MMRC）模式、 變質心配平控制（MMTC）模式難以實現飛行器三個通道的姿態控制需求。 因此， 變質心與其他控制手段結合， 充分發揮不同控制手段優勢， 實現變質心復合控制（MMPC）模式就成為變質心控制發展的必然選擇。

變質心與其他手段復合主要有兩種方式： 變質心與其他手段分通道并行復合、 變質心與其他手段分時段串行復合。 分通道并行復合， 是指變質心與其他控制手段在時間尺度上并行， 用于實現飛行器不同通道姿態控制的復合模式。 如Li等[26]提出的大質量比變質心配置用于實現飛行器俯仰姿態控制， 而滾轉姿態控制和偏航姿態鎮定則依賴飛行器尾部安裝的直接力裝置。 文獻[27]為高超聲速無動力滑翔飛行器配置兩個可動質量塊實現俯仰和偏航通道姿態控制， 配置一對副翼實現滾轉通道姿態控制， 實現了變質心/氣動力分通道并行復合。 分時段串行復合， 是指變質心與其他控制手段在時間尺度上串行， 用于實現飛行器相同通道姿態控制的復合模式。 如王霄婷等[28]針對再入飛行器高空飛行動壓過低問題， 高空段采用直接力實現姿態控制， 隨著飛行高度降低， 逐漸過渡到采用變質心實現姿態控制， 對變質心/直接力分時段串行復合策略進行了研究。

總之， 變質心復合控制（MMPC）能夠有效應對不斷復雜的飛行任務需求， 充分發揮不同控制手段優勢， 實現控制效能優化， 是具有潛力的控制模式。

4 變質心技術展望

當前， 變質心技術主要研究應用于再入飛行器、 制導彈藥、 動能攔截器等高速飛行器的姿態控制中。 但隨著人類航天活動范圍擴大， 飛行控制對象多樣化， 變質心技術的應用場景和應用對象也將進一步擴充。 一方面， 應深入研究突破變質心技術應用的關鍵難點問題; 另一方面， 結合變質心技術優勢， 充分開拓思路， 為變質心技術應用打開更廣闊的空間。

4.1 難點問題

變質心控制具有傳統氣動舵等控制手段無法比擬的優勢， 但也面臨著諸多關鍵難點問題， 主要包括： 復雜多體動力學建模、 強耦合強非線性控制、 高動態高性能執行機構設計與研制等問題。 這些關鍵難點問題的研究突破將直接影響變質心技術未來發展與應用。

采用變質心技術的飛行器不再滿足單剛體假設條件， 屬于多剛體動力學范疇， 數學模型復雜。 在某些情況下還需要考慮變質心飛行器彈性變形[29]， 如具有長細比或楔形布局的飛行器， 此時， 飛行器多體動力學模型更加復雜， 運動耦合作用顯著。 充分考慮變質心飛行器復雜多體動力學特性， 建立高精度全量數學模型， 是開展變質心技術研究與應用的首要任務。

變質心飛行器可移動質量塊運動帶來了更加嚴重的控制耦合、 慣量耦合以及軌跡/姿態耦合問題。 同時， 受飛行器內部空間限制等， 變質心飛行器存在欠驅動控制、 抗飽和控制等非線性控制問題[30]， 研究適用于變質心飛行器的強耦合非線性控制方法， 對于發揮變質心技術優勢具有重要意義。

變質心執行機構設計要在考慮飛行器內部空間約束的前提下滿足變質心實施方案的具體需求， 避免多質量塊運動干涉， 提高質量塊質量比和行程范圍， 保證需用控制能力。 同時， 由于飛行器高動態、 高過載特點， 飛行器變質心執行機構也應具有高動態、 高效率、 抗高過載等性能， 這就給變質心執行機構的高效傳動和高性能伺服提出要求。

4.2 應用展望

基于變質心技術優勢， 結合不斷提升的航天活動需求， 未來變質心技術有望應用于更多場景和對象。

變質心技術應用于火星探測領域。 變質心控制作為一種低費效比控制方式， 可用于火星探測器再入段飛行控制， 一方面充分利用火星大氣環境特性， 另一方面可以減少燃料攜帶量， 對于火星探測等深空探測任務具有重要意義[31]。 已有研究人員以美國NASA火星探測器為對象， 開展了基于多個可動質量塊的變質心火星再入段姿態控制技術研究[32]。

變質心技術應用于平流層飛艇， 能夠有效支撐其長航時對地觀測等任務[33]。 平流層飛艇具有體積大、 內部空間充足的特點， 特別適合于需配置可動質量塊實現高效控制的變質心技術。 文獻[34]針對平流層飛艇配置圓弧軌道雙質量塊， 實現了俯仰/滾轉通道姿態聯合控制， 并對變質心應用于平流層飛艇的控制能力影響因素進行了分析。

變質心技術應用于低空無人機， 能夠有效提高氣動效率、 降低翼面結構復雜性等[35-36]。 研究表明， 變質心固定翼無人機姿態控制系統具有較強魯棒性和抗干擾能力， 能有效應對無人機飛行過程中所面臨的各類復雜狀況[37]。 此外， 小型電動旋翼無人機的變質心姿態控制也具有足夠高的可操縱性， 適用于航空運輸、 攝影、 監視、 搜索救援等任務[38]。

變質心技術應用于小型航天器， 有望以低成本、 高效率解決微納衛星、 立方星可控性差， 而傳統控制系統過于復雜等問題。 Huang等[39]就提出利用太陽航行CubeSat受到的太陽輻射壓力與CubeSat主動移動產生的變質心控制扭矩， 實現太陽帆姿態操縱和太陽指向穩定的方法。 陸正亮等[40-41]研究了應用變質心技術實現納衛星軌道機動過程中的姿態穩定控制問題， 回避了常用多噴嘴小推力的姿控發動機系統復雜、 成本高的問題。

不難發現， 由于變質心技術相比于其他傳統控制手段的優越性， 其將在深空探測、 對地觀測、 通用航空等未來航空航天任務中大有用武之地。

參考文獻：

[1] 謝佐慰. 美國機動彈頭技術發展概況[J]. 國外導彈技術， 1984（3）： 1-24.

Xie Zuowei. Development of Motorized Warhead Technology in the United States[J]. Foreign Missile Technology， 1984（3）： 1-24. （in Chinese）

[2] Petsopoulos T， Regan F J， Barlow J. Moving-Mass Roll Control System for Fixed-Trim Re-Entry Vehicle[J]. Journal of Spacecraft and Rockets， 1996， 33（1）： 54-60.

[3] Norris R S， Kristensen H M. Russian Nuclear Forces[J]. Bulletin of the Atomic Scientists， 2005， 61（2）： 70-72.

[4] 崔利明. 旋轉彈頭變質心機動控制、 制導系統的研究和仿真[D]. 西安： 西北工業大學， 2000.

Cui Liming. Study and Simulation of Control and Guidance System of Spinning Maneuver Warhead with Variable-Centroid[D]. Xi’an： Northwestern Polytechnical University， 2000. （in Chinese）

[5] 周鳳岐， 易彥， 周軍. 克服旋轉導彈螺旋運動的方法研究[J]. 宇航學報， 2001， 22（5）： 77-81.

Zhou Fengqi， Yi Yan， Zhou Jun. Research on Overcoming the Coning Motion of Rotary Missile[J]. Journal of Astronautics， 2001， 22（5）： 77-81. （in Chinese）

[6] 易彥， 周鳳岐.? 高超聲速戰術導彈的變質心矢量控制[J]. 中國科學（G輯）， 2003， 33（3）： 281-288.

Yi Yan， Zhou Fengqi. Variable Centroid Vector Control of Hypersonic Tactical Missile[J]. Science in China（Series G）， 2003， 33（3）： 281-288. （in Chinese）.

[7] 耿克達. 二維變質心機構半物理仿真平臺設計[D]. 西安： 西北工業大學， 2011.

Geng Keda. Design of Semi-Physical Simulation Platform for Two-Dimensional Moving Mass Mechanism[D]. Xi’an： Northwestern Polytechnical University， 2011. （in Chinese）.

[8] 虞天曄. 稀薄大氣下高速飛行器二維變質心/RCS復合控制系統設計[D]. 西安： 西北工業大學， 2018.

Yu Tianye. The Two-Dimensional Moving-Mass/RCS Compound Control System for High-Speed Vehicle in Thin Atomosphere[D]. Xi’an： Northwestern Polytechnical University， 2018. （in Chinese）

[9] 陳浩嵐. 高超聲速飛行器二維變質心控制系統設計[D]. 西安： 西北工業大學， 2019.

Chen Haolan. The Two-Dimensional Moving-Mass Control System Design for Hypersonic Vehicles[D]. Xi’an： Northwestern Polytechnical University， 2019. （in Chinese）.

[10] 王丹妮. 變質心飛行器控制方法研究[D]. 哈爾濱： 哈爾濱工業大學， 2018： 29-43.

Wang Danni. Control Method for a Moving-Mass Vehicle[D]. Harbin： Harbin Institute of Technology， 2018： 29-43.（in Chinese）

[11] 王林林. 再入飛行器制導與控制方法研究[D]. 北京： 北京理工大學， 2016： 4.

Wang Linlin. Research on Guidance and Control System of a Reentry Vehicle[D]. Beijing： Beijing Institute of Technology， 2016： 4.（in Chinese）

[12] 劉智陶， 李澗青， 高長生. 欠驅動變質心飛行器的滾偏耦合自抗擾控制[J]. 北京航空航天大學學報， 2021， 47（2）： 281-288.

Liu Zhitao， Li Jianqing， Gao Changsheng. ADRC-Based Roll-Yaw Coupling Control of Underactuated Moving Mass Flight Vehicles[J]. Journal of Beijing University of Aeronautics and Astronautics， 2021， 47（2）： 281-288.（in Chinese）

[13] 周敏， 周軍， 盧明飛. 一種面向固定配平型彈頭的螺旋機動控制方法[J]. 宇航學報， 2017， 38（11）： 1195-1203.

Zhou Min， Zhou Jun， Lu Mingfei. A Spiral-Maneuver Control Method for a Fixed-Trim Warhead[J]. Journal of Astronautics， 2017， 38（11）： 1195-1203.（in Chinese）

[14] Dong K X， Zhou J， Zhou M， et al. Roll Control for Single Moving-Mass Actuated Fixed-Trim Reentry Vehicle Considering Full State Constraints[J]. Aerospace Science and Technology， 2019， 94： 105365.

[15] Wang Y F， Yu J Q， Mei Y S， et al. Nonlinear Dynamics of Fixed-Trim Reentry Vehicles with Moving-Mass Roll Control System[J]. Journal of Systems Engineering and Electronics， 2016， 27（6）： 1249-1261.

[16] 范一迪， 荊武興， 高長生， 等. 滾控式變質心飛行器動力學特性分析與控制[J]. 宇航學報， 2019， 40（4）： 386-395.

Fan Yidi， Jing Wuxing， Gao Changsheng， et al. Analysis of Dynamics Characteristics and Control of a Flight Vehicle with a Moving-Mass Roll Control System[J]. Journal of Astronautics， 2019， 40（4）： 386-395.（in Chinese）

[17] Su X L， Yu J Q， Wang Y F， et al. Moving Mass Actuated Reentry Vehicle Control Based on Trajectory Linearization[J]. International Journal of Aeronautical and Space Sciences， 2013， 14（3）： 247-255.

[18] 劉智陶. 單滑塊滾控式變質心高超聲速飛行器制導控制[D]. 哈爾濱： 哈爾濱工業大學， 2019： 40-47.

Liu Zhitao. Guidance and Control of Hypersonic Flight Vehicle with a Single Roll-Control Moving Mass[D]. Harbin： Harbin Institute of Technology， 2019： 40-47.（in Chinese）

[19] Regan F J， Kavetsky R A. Add-On Controller for Ballistic Reentry Vehicles： US， 752766 [P]. 1984.

[20] Robinett R D， Sturgis B R， Kerr S A. Moving Mass Trim Control for Aerospace Vehicles[J]. Journal of Guidance， Control， and Dynamics， 1996， 19（5）： 1064-1070.

[21] Zheng Q S， Zhou Z M. Stability of Moving Mass Control Spinning Missiles with Angular Rate Loops[J]. Mathematical Problems in Engineering， 2019， 2019：1-10.

[22] Menon P K， Sweriduk G D， Ohlmeyer E J， et al. Integrated Guidance and Control of Moving-Mass Actuated Kinetic Warheads[J]. Journal of Guidance， Control， and Dynamics， 2004， 27（1）： 118-126.

[23] Chen H L， Zhou J， Zhou M， et al. Nussbaum Gain Adaptive Control Scheme for Moving Mass Reentry Hypersonic Vehicle with Actuator Saturation[J]. Aerospace Science and Technology， 2019， 91： 357-371.

[24] Gao C S， Jing W X， Wei P X. Research on Application of Single Moving Mass in the Reentry Warhead Maneuver[J]. Aerospace Science and Technology， 2013， 30（1）： 108-118.

[25] 李澗青. 單質量塊變質心飛行器動力學與控制問題研究[D]. 哈爾濱： 哈爾濱工業大學， 2018： 22.

Li Jianqing. Research on Dynamic and Control for Single Moving Mass Flight Vehicle[D]. Harbin： Harbin Institute of Technology， 2018： 22. （in Chinese）.

[26] Li J Q， Chen S， Li C Y， et al. Adaptive Control of Underactuated Flight Vehicles with Moving Mass[J]. Aerospace Science and Technology， 2019， 85： 75-84.

[27] 李瑞康， 荊武興， 高長生， 等. 再入彈頭質量矩復合控制系統設計[J]. 航天控制， 2009， 27（4）： 43-48.

Li Ruikang， Jing Wuxing， Gao Changsheng， et al. Control System Design for Reentry Warhead with Mass Moment Compound Actuate[J]. Aerospace Control， 2009， 27（4）： 43-48.（in Chinese）

[28] 王霄婷， 周軍， 林鵬. 再入飛行器變質心/RCS復合控制策略研究[J]. 西北工業大學學報， 2011， 29（2）： 212-216.

Wang Xiaoting， Zhou Jun， Lin Peng. Proposing Moving Centroid/RCS Control Strategy for Reentry Flight Vehicle[J]. Journal of Northwestern Polytechnical University， 2011， 29（2）： 212-216.（in Chinese）

[29] Wang X M， Zhou W Y， Mu R N， et al. Modeling and Simulation of Mass-Actuated Flexible Aircraft for Roll Control[J]. Aerospace Science and Technology， 2020， 107： 106254.

[30] Wei P X， Gao C S， Jing W X. Longitudinal Aerodynamic Coefficients Estimation and Identifiability Analysis for Hypersonic Glider Controlled by Moving Mass[J]. International Journal of Aeronautical and Space Sciences， 2019， 20（1）： 31-43.

[31] Yuan J L， Ni K， Zhang Q Z， et al. Modeling of Mars Entry Vehicles with an Internal Sole-Moving-Mass Actuator[C]∥IEEE CSAA Guidance， Navigation and Control Conference （CGNCC）， 2018： 1-6.

[32] Atkins B M， Queen E M. Internal Moving Mass Actuator Control for Mars Entry Guidance[J]. Journal of Spacecraft and Rockets， 2015， 52（5）： 1294-1310.

[33] Chen L， Gao Q， Deng Y， et al. Moving-Mass-Based Station Keeping of Stratospheric Airships[J]. The Aeronautical Journal， 2021， 125（1289）： 1231-1244.

[34] 陳麗， 周革， 段登平. 平流層飛艇變質心姿態運動仿真[J]. 系統仿真學報， 2012， 24（12）： 2434-2438.

Chen Li， Zhou Ge， Duan Dengping. Simulation of Moving-Mass Control of Stratospheric Airship[J]. Journal of System Simulation， 2012， 24（12）： 2434-2438.（in Chinese）

[35] Haus T， Orsag M， Bogdan S. Mathematical Modeling and Control of an Unmanned Aerial Vehicle with Moving Mass Control Concept[J]. Journal of Intelligent & Robotic Systems， 2017， 88（2/3/4）： 219-246.

[36] Brown R. Trim Analysis for an Electric Rotorcraft Utilizing a Moving Mass Control Scheme[C]∥AIAA Scitech 2020 Forum， 2020.

[37] 邱瀟頎， 高長生， 荊武興. 變質心固定翼無人機動力學分析與抗擾控制[J/OL].北京航空航天大學學報， 2021.https：∥doi.org/10.13700/j.bh.1001-5965.2020.0573.

Qiu Xiaoqi， Gao Changsheng， Jing Wuxing. Dynamic Analysis and Control of Mass-Actuated Fixed-Wing UAV[J/OL].Journal of Beijing University of Aeronautics and Astronautics， 2021. https：∥doi.org/10.13700/j.bh. 1001-5965.2020.0573. （in Chinese）

[38] Darvishpoor S， Roshanian J， Tayefi M. A Novel Concept of VTOL Bi-Rotor UAV Based on Moving Mass Control[J]. Aerospace Science and Technology， 2020， 107： 106238.

[39] Huang H， Zhou J. Solar Sailing Cube Sat Attitude Control Method with Satellite as Moving Mass[J]. Acta Astronautica， 2019， 159： 331-341.

[40] 陸正亮，張翔，于永軍， 等. 納衛星變軌段質量矩姿態控制系統設計[J]. 航空學報， 2017， 38（6）： 320778.

Lu Zhengliang， Zhang Xiang， Yu Yongjun， et al. Design of Moving-Mass Attitude Control System for Nanosatellites in Orbital Transfer Stage[J]. Acta Aeronautica et Astronautica Sinica， 2017， 38（6）： 320778.（in Chinese）

[41] Lu Z L， Hu Y D， Liao W H， et al. Modeling and Attitude Control of Cube Sat Utilizing Moving Mass Actuators[J]. Advances in Space Research， 2021， 67（1）： 521-530.

Development and Application of Moving Mass Control Technology

Zhou Min*， Zhou Fengqi， Zhou Jun， Guo Jianguo

（Institute of Precision Guidance and Control， Northwestern Polytechnical University， Xi’an 710072， China）

Abstract： The moving mass technology uses the movement of the internal masses to change the position of the mass center of vehicles. It can avoid thermal ablation， rudder flutter， and high fuel consumption caused by traditional manners such as aerodynamic rudder and reaction control system. It is of high control efficiency and advantageous to maintain a good aerodynamic configuration for vehicles. Based on the connotation of moving mass control， this paper summarizes the characteristics of the two forms of moving mass configuration. The research progress of three moving mass control modes， including roll control， trim control and compound control， is sorted out. Finally， key problems faced by the moving mass technology， such as complex multi-body dynamics modeling， strong coupling and strong nonlinear control， design and development of high dynamic and high performance actuator， are discussed. By looking forward to the new scenarios of moving mass control application， the future research direction is pointed out.

Key words： moving mass; configuration form; roll control; trim control; compound control; flight control