中考“面積問題”的教學實踐與思考

問題是數學的心臟，學習數學的主要目的在于解決問題。好的數學問題應與學生的實際生活有著直接的聯系，應當具有較強的探索性、現實意義和趣味性以及知識性。面積問題是數學知識結構中的“連結點”，其常結合一次函數、反比例函數、二次函數、三角形全等和相似、四邊形、圓等初中數學核心內容成為考試試題。

一、認識：面積問題的類型

面積問題為學生提供了一個觀察、分析、猜想并進行說理驗證的探究模型，以圖形的運動變化為策略，使學生能在一個動態(tài)的數學情境中感悟知識的發(fā)生和發(fā)展過程，探索問題的結論和規(guī)律的變化，真正理解圖形的性質。

1.公式法

例1.如圖，將一塊三角板和半圓形量角器按圖中方式疊放，三角板一邊與量角器的零刻度線所在直線重合，重疊部分的量角器弧對應的圓心角(∠AOB)為120°，OC 的長為2cm，則三角板和量角器重疊部分的面積為_____。

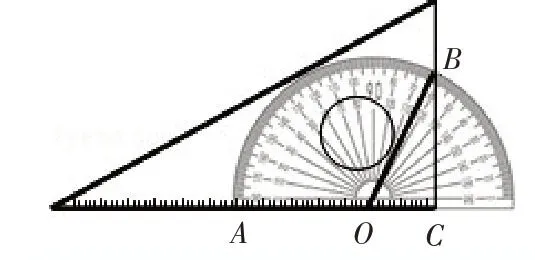
分析：在Rt△OBC中求出OB、BC，然后求出扇形OAB及△OBC的面積即可得出答案。本題考查了扇形的面積計算，解答本題關鍵是求出扇形的半徑，熟練掌握扇形的面積公式。

面積問題，有的是直接計算面積，有的是以面積為條件求其他，更多的情況是由圖形的運動引起圖形的變化，從而建立面積函數關系。中考命題中如何從具體情境中抽象出數學材料，并將獲得的材料符號化，體現基礎性、應用性、實踐性、開放性、探究性，這是中考數學試題的重要特征。

2.割補法

例2.如圖，AE是半圓O的直徑，弦，弦CD=DE=4，連結OB、OD，則圖中兩個陰影部分的面積和為____。

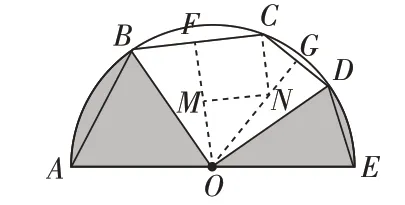
分析：根據弦AB=BC，CD=DE，可得∠BOD=90°，過點O作OF⊥BC于點F，OG⊥CD于點G，在四邊形OFCG中可得∠FCD=135°，過點C作CN∥OF，交OG于點N，判斷△CNG、△OMN為等腰直角三角形，分別求出NG、ON，繼而得出OG，在Rt△OGD中求出OD，即得圓O的半徑，代入扇形面積公式求解即可。

學習數學知識是學生主動構建知識體系的過程，學生只有通過自身的操作活動和主動參與學習的數學才是有效的。在學生動手操作、探究的過程中，逐步形成分析、判斷、推理、歸納、表達等能力。

3.整體法

例3.如圖，CD是⊙O的直徑，弦AB⊥CD，垂足為點M，AB=20，分別以CM、DM為直徑作兩個大小不同的⊙O1和⊙O2，則圖中陰影部分的面積為____(結果保留π)。

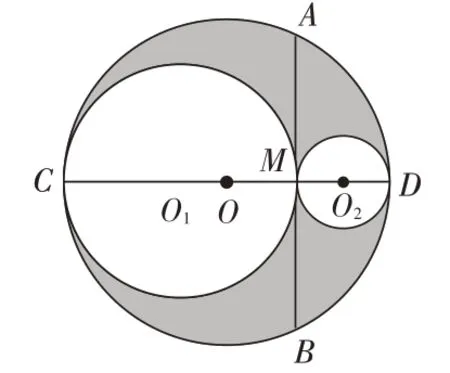
分析：因為題目中沒有告知⊙O1和⊙O2的半徑大小，說明所求陰影部分的面積與其大小是沒有關系的，這是一道選擇題，在考試的時候，直接計算顯然是不可取的，計算量大，費時且容易出錯，可用特殊值法整體考慮求解。

二、實踐：面積問題的解題策略

數學來源于生活，同時也必將應用于生活，學數學就是為了解決生活中所碰到的實際問題。近幾年的中考題相當注重運用數學知識解決實際問題的考查，考查層次非常豐富，不同水平的學生可以充分展示自己不同的探究深度，以及綜合運用數學知識、思想方法去探索規(guī)律、獲取新知的能力。

例4.如圖，直線l1⊥x軸于點A(2，0)，點B是直線l1上的動點。直線l2：y=x+1 交l1于點C，過點B作直線l3垂直于l2，垂足為D，過點O、B的直線l4交l2于點E。當直線l1、l2、l3能圍成三角形時，設該三角形面積為S1，當直線l2、l3、l4能圍成三角形時，設該三角形面積為S2。1.若點B在線段AC上，且S1=S2，則B點坐標為__▲__；2.若點B在直線l1上，且，則∠BOA的度數為__▲__。

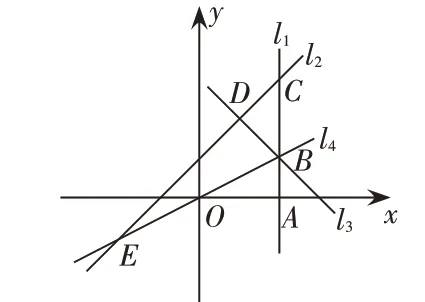
分析：1.設B的坐標是(2，m)，則△BCD是等腰直角三角形，即可表示出S1，求得直線l1的解析式，解方程組即可求得E的坐標，則S2的值即可求得，根據S1=S2，即可得到一個關于m的方程從而求得m的值；2.根據，即可得到一個關于m的方程從而求得m的值，得到AB的長，從而求得∠BOA的正切值，求得角的度數。

“能使學生獲得受用終生的東西的教育，才是最高尚最好的教育。”數學思想方法的教學，正是這樣一件富有意義的工作。對于學生來說，不論將來從事什么工作，唯有深深地銘刻于頭腦中的數學精神、數學的思維方法、研究方法，可以隨時隨地會發(fā)生作用，使他們受益終生。