城市LED屏幕光污染影響評價及防治初探
許 琰(沈陽城市建設(shè)學院,遼寧沈陽,110167)
?
城市LED屏幕光污染影響評價及防治初探
許 琰
(沈陽城市建設(shè)學院,遼寧沈陽,110167)
摘要:隨著我國現(xiàn)代化城市建設(shè)的不斷推進,城市中LED屏幕的光污染問題日益受到人們的關(guān)注和重視。本文從光污染的定義與分類出發(fā),論述LED屏幕光污染的危害和其光污染影響評價因素,并提出LED屏幕光污染的防治對策,以期引起人們對光污染的重視,為相關(guān)政府職能部門制定法律法規(guī)、標準等提供了一些參考。
關(guān)鍵詞:LED屏幕;光污染;影響評價因素;防治措施
0 引言
近年來,LED 顯示屏技術(shù)飛速發(fā)展,憑借其表現(xiàn)力更強,傳播效果好,價格逐漸下降的優(yōu)勢已廣泛地應(yīng)用于各行各業(yè),各大城市LED顯示屏如雨后春筍般豎立在街頭巷尾。可是隨著LED顯示屏增多,LED顯示屏產(chǎn)生的“光污染”問題越來越多,并引起了廣泛的重視。
1 光污染的定義與分類
光污染泛指影響自然環(huán)境,對人類正常生活、工作、休息和娛樂帶來不利影響,損害人們觀察物體的能力,引起人體不適感和損害人體健康的各種光。在我國頒布的行業(yè)標準《城市夜景照明設(shè)計規(guī)范》中“光污染”的定義是干擾光或過量的光輻射(含可見光、紫外和紅外光輻射)對人、生態(tài)環(huán)境和天文觀測等造成的負面影響的總稱。一般將現(xiàn)代社會產(chǎn)生的過量的或不適當?shù)墓廨椛鋵θ祟惿詈蜕a(chǎn)環(huán)境所造成的不良影響的現(xiàn)象統(tǒng)稱為“光污染”。
光污染主要有以下幾類:
(1)眩光污染:眩光是指由于視野中的亮度分布或亮度范圍的不適宜, 或存在極端的對比, 以致引起不舒適感覺或降低觀察細部或目標的能力的視覺現(xiàn)象。
(2)輻射污染:目前在城市燈光建設(shè)中廣泛使用的大功率光源在發(fā)出可見光的同時也輻射出非可見的射線,這些射線的一部分對人體或建筑材料具有損害作用,主要表現(xiàn)為紫外輻射和紅外輻射(熱輻射)。
(3)光泛濫:光泛濫表現(xiàn)在宏觀上,使城市天空溢散光水平提高,導致夜空發(fā)亮;在微觀上,表現(xiàn)為光線的過量溢散。光泛濫可歸結(jié)為光誤用和光干擾兩個方面。
(4)視單調(diào):視覺單調(diào)表現(xiàn)為空間單調(diào)、色彩單調(diào)和光形單調(diào)等。
(5)視遮蔽:視遮蔽是人的視界被不適當?shù)恼诒蔚默F(xiàn)象,包括燈光遮蔽和燈光設(shè)施遮蔽。
(6)頻閃:頻閃指在以一定頻率(通常在50Hz下)變化的光的照射下,觀察到物體運動顯現(xiàn)出不同于實際運動的現(xiàn)象。
2 LED 顯示屏產(chǎn)生光污染的危害
LED屏幕產(chǎn)生光污染對屏幕周邊生態(tài)系統(tǒng)的各個層面產(chǎn)生多種危害,主要表現(xiàn)為對周邊人群、動植物、交通等產(chǎn)生或大或小的影響,其主要表現(xiàn)在以下幾方面:
2.1對附近居民的影響
當LED屏幕射出光線直接侵入附近居民的窗戶時,就很可能對居民的正常生活產(chǎn)生負面的影響。這些影響包括:入夜后LED屏幕發(fā)出光線使居民的睡眠受到影響。LED屏幕播放畫面產(chǎn)生頻繁閃爍的光線使房屋內(nèi)的居民感到煩躁,難以進行正常的活動。
2.2對附近行人的影響
當?shù)缆放訪ED屏幕設(shè)備安裝不合理時,會對附近的行人產(chǎn)生眩光,當屏幕畫面切換時會瞬間降低或完全喪失正常的視覺功能。這一方面影響到行人對周圍環(huán)境的認知,同時增加了發(fā)生交通事故的危險性。并且當LED屏幕本身的亮度照射路面等處產(chǎn)生的高亮度反射面出現(xiàn)在行人的視野范圍內(nèi)時,因為出現(xiàn)很大的亮度對比,行人將無法看清周圍較暗的地方,使之成為盲區(qū),從而產(chǎn)生道路交通安全隱患。
3 LED屏幕光污染環(huán)境影響評價的幾個因素
(1)光強:發(fā)光強度簡稱光強,國際單位是candela(坎德拉)簡寫cd。對于LED顯示屏這種主動發(fā)光體一般采用cd·m-2 作為發(fā)光強度單位,并配合觀察角度為輔助參數(shù),其等效于屏體表面的照度單位勒克司;將此數(shù)值與屏體有效顯示面積相乘,得到整個屏體的在最佳視角上的發(fā)光強度,假設(shè)屏體中每個像素的發(fā)光強度在相應(yīng)空間內(nèi)恒定,則此數(shù)值可被認為也是整個屏體的光通量。
(2)光的頻閃度:電光源頻閃是指電光源光通量波動的深度。當電光源的光通量波動深度越大,頻閃越嚴重。光的閃爍會引發(fā)視覺疲勞、偏頭痛,造成人眼分辯能力下降,視力下降,還會引發(fā)心跳過速等,這種現(xiàn)象稱為頻閃效應(yīng)(或閃爍現(xiàn)象)。有時光源的發(fā)光強度并不大,但它不斷閃爍,造成視覺混亂,產(chǎn)生了光污染。光的閃爍度可以用Hz每秒所閃爍的次數(shù)(次/秒)來計量。人眼最敏感的閃爍頻率是8. 8Hz,當閃爍40Hz 以上感覺就不靈敏,至50Hz 以上時則完全感覺不到。
(3)光照與周邊環(huán)境的對比度,同樣的光照強度和頻閃度的情況下,如果與周邊環(huán)境照度的對比越大,產(chǎn)生光污染的強度就越大,例如同樣的LED屏幕在白天觀看并不是十分刺眼,而在夜晚觀看卻十分刺眼。
目前國內(nèi)外學者大多認為對光污染評價應(yīng)通過對上述指標的綜合評定來確定光污染的等級。例如國際照明學會(CIE)對住宅干擾光照度和光強均有嚴格的規(guī)定,并對相關(guān)區(qū)域宵禁前后照度和光強進行了限定,如表1 所示。
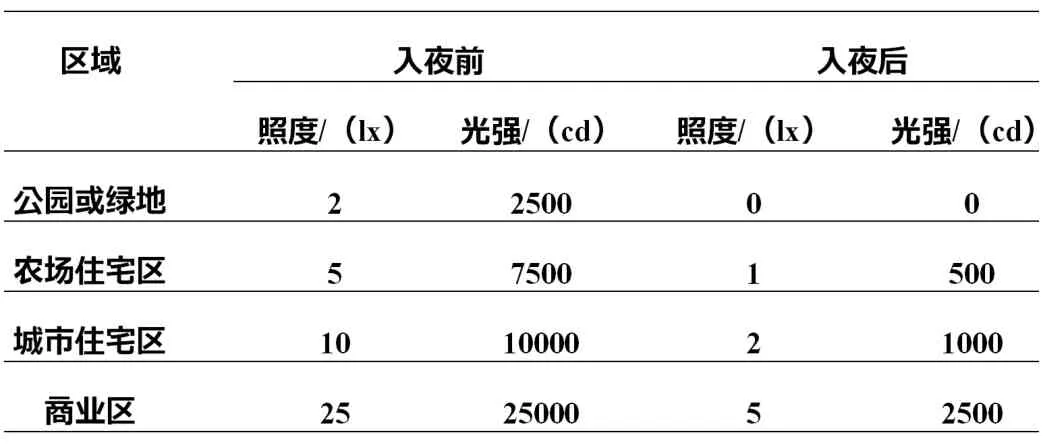
表1 CIE對相關(guān)區(qū)域入夜前后照度和光強的限定
在國內(nèi)上海市質(zhì)量技術(shù)監(jiān)督局發(fā)布《城市環(huán)境(裝飾)照明規(guī)范》 DB31/T 316-2004中對廣告、招牌的最大允許亮度的限值的相關(guān)內(nèi)容(見表2)。

表2 商業(yè)中心區(qū)內(nèi)的廣告、招牌的最大允許亮度[注]
北京和南京等大城市都出臺了《戶外電子顯示屏設(shè)置規(guī)范》,規(guī)定在商業(yè)區(qū)及其周邊設(shè)置的戶外電子顯示屏,夜間亮度值應(yīng)不大于1000 cd·m-2;在其他地區(qū)設(shè)置的戶外電子顯示屏,夜間亮度值應(yīng)不大于400 cd·m-2。
所以根據(jù)上述指標我們可以得出當LED屏幕的光強超出表中所列強度時。認為會產(chǎn)生光污染,且超出越高,產(chǎn)生光污染的強度越高。
同時LED屏幕的光強與周邊環(huán)境的照度對比同樣也是影響光污染的重要因素,相同的光強下,當與周邊環(huán)境照度對比強烈是,光污染的強度會增大。根據(jù)對人群進行主觀感覺測試的得出不同環(huán)境照度下屏幕光強的臨界值(見表3),當光強超過臨界值時,人們會感覺刺眼和不適。

表3 不同環(huán)境照度下屏幕光強的臨界值
LED屏幕播放靜止畫面是本身刷新都高于50HZ對人眼影響不大,但在播放動態(tài)畫面時,特別是在切換對比強烈的畫面時會產(chǎn)生閃爍感,對人眼刺激較大,所以LED播放動態(tài)畫面應(yīng)避免強對比度畫面的切換,切換畫面要柔和,減少對人眼的刺激。
綜上所述,LED屏幕對環(huán)境產(chǎn)生光污染的因素主要有LED屏幕的光強、屏幕光強與周邊環(huán)境的對比度、LED屏幕播放內(nèi)容產(chǎn)生的頻閃度幾個方面。
4 減少LED屏幕產(chǎn)生光污染的幾個措施
4.1LED屏幕亮度控制
LED屏幕亮度對人眼的影響是隨周邊環(huán)境的亮度影響的,同樣的屏幕亮度在白天,人們看起來并不刺眼,而到了夜間或光照不好時就顯得十分刺眼。所以建議LED屏幕增加亮度自適應(yīng)調(diào)節(jié)的功能,通過對周邊環(huán)境亮度的感知,自動調(diào)節(jié)LED屏幕本身的亮度,從而減少取所產(chǎn)生的光污染同時也可以達到節(jié)約能源的效果。
4.2LED屏幕播放內(nèi)容評估
LED屏幕在頻繁切換大對比度,色彩鮮艷的畫面時,會給人眼帶來頻繁閃爍的效果,所以對LED屏幕播放的內(nèi)容應(yīng)進行評估與控制,對色彩對比度大的畫面要采取漸進切換的方式,同時播放動態(tài)畫面時適當降低播放速度,減少對人眼的刺激。
4.3特殊時段或條件下關(guān)閉大屏幕
為了減少LED屏幕光源對周圍居民和行人的影響,在特殊的時段如:深夜,由于LED屏幕的光線會影響周邊居民的睡眠。特殊天氣,如雨天,LED屏幕的光線投射到路面會產(chǎn)生較強的反射應(yīng)用駕駛員看清路面,所以在每天的特殊時段和特殊天氣條件線關(guān)閉大屏幕以減少屏幕對周邊環(huán)境帶來的影響。
5 結(jié)語
光污染已成為21世紀人們關(guān)注的問題,城市越來越多的LED屏幕已從多個方面影響著人們的生活和工作環(huán)境,現(xiàn)已引起廣泛的重視與關(guān)心。LED光污染環(huán)境影響評價是LED屏幕建設(shè)項目環(huán)境管理的一項新內(nèi)容。目前我國對LED屏幕的光污染評價還沒有建立起一套完善的統(tǒng)一的指標、標準。希望本文可以為相關(guān)政府職能部門制定法律法規(guī)、標準等提供了一些參考。
參考文獻
[1]Jari L,Petri T,Timo A.Unawareness in environmental protection:the case of light pollution from traffic [J].Land Use Policy,2012,29( 3):598-604.
[2] 劉潔,彭曉春,鐘齊佳等.關(guān)于城市光污染控制管理對策探討[J],環(huán)境與可持續(xù)發(fā)展,2012,6(4):64-68.
[3] 周倜.城市夜景照明光污染問題及設(shè)計對策[D],武漢:華中科技大學[碩士論文],2004.
Preliminary study on Evaluation and prevention measures of city LED screen light pollution
Xu Yan
(Shenyang Urban Construction University,Department of Basic,110167)
Abstract:As China's urban construction developing,city LED screen light pollution of urban has increasingly come under people's concern and attention.This paper first discusses the definition and classification of light pollution,and discusses LED screen light pollution and light pollution impact assessment factors, lastly discusses LED screen light pollution prevention measures,to draw attention to light pollution,for the relevant authorities to make laws,regulations,standards provide some reference.
Keywords:LED screen;Light Pollution;environmental impact assessment factor;Prevention and control measures

