100 t鋼包流場物理及數值模擬研究

郝曉倩，高立福，崔 振，武光君，劉春偉，屈天鵬

（1 山鋼股份萊蕪分公司，山東 濟南271104；2 蘇州大學沙鋼鋼鐵學院，江蘇 蘇州215021）

1 前 言

鋼包又稱為大包，是用于盛放鋼液并進行精煉和澆注的容器［1］。鋼鐵連鑄是一個高溫、不可見、復雜的冶金過程，鋼包是連鑄的主要容器之一，因此物理模擬和基于fluent的數值模擬在鋼包流場研究中具有重要意義。

2 物理試驗研究

2.1 物理試驗原理

鋼包中鋼液的流動，是鋼液在重力作用下從鋼包水口流入中間包，在這種情況下，一般可視為黏性不可壓縮穩態流動，同時可以忽略化學反應的影響，因此在進行流動模擬研究時，系統主要滿足幾何相似和動力相似［2］。

幾何相似，即模型與其原型形狀相同，但尺寸可以不同，而一切對應的線性尺寸成比例，這里的線性尺寸可以是直徑、長度及粗糙度等。本試驗中鋼包模型（Lm）與實際（Lp）的幾何尺寸相似比選擇為1∶3［3］。

動力相似，用水作為介質模擬鋼液，水和鋼液的物理性質如表1 所示。因為水的運動黏度與鋼液的運動黏度相當。動力相似要求模型和原型中流體的雷諾準數Re 和付魯德準數Fr 分別相等，但是在試驗過程中，同時滿足模型和原型的雷諾準數Re 和付魯德準數Fr 相等是相當困難的。根據流體力學原理，當流體流動的Re 數大于第二臨界值時，流體的湍動程度及流速的分布幾乎不再受雷諾數的影響，也就是說流體流動進入第二自模化區域。一般雷諾數的第二自模化區的臨界值為1×104～1×105，此時，只考慮Fr 數相等，即能夠滿足動力相似［4］。

表1 水和鋼液的物理性質

鋼包底吹氬促使鋼液體系流動主要作用力是氣泡的浮力，而非湍流的粘滯力。考慮物理模擬試驗滿足模型及原型的Fr’相等，以保證模型與原型之間的動力相似。依此可以確定模型鋼包中底吹氣量的設計范圍［5］。

相似準數Fr’定義為：

式中：u為特征速度，m/s；H為熔池深度，m；ρ1、ρg為液體和氣體的密度，kg/m3；g為重力加速度，9.81 m/s2。

特征速度u可由下式給出：

式中：Q為氣體體積流量，m3/h；d為底吹噴嘴直徑，m。聯立上式，由Frm’=Frp’可得：

經過對氣體密度的修正可得：

式中：Qm、QP分別為模型和原型供氣流量，m3/h。

將修正參數代入上式可得模型與原型底吹氣量的關系式為：

2.2 物理模擬試驗方法

物理模擬試驗采用“刺激－響應”原理。其方法為：在冶金容器注入流處輸入一個刺激信號，信號一般使用示蹤劑來實現，然后在容器出口處測量該信號的輸出，即所謂響應，從響應曲線分析其流動狀況及其對冶金反應的影響。

在冷態模擬試驗中，通常使用電解質、發光或染色物質作為示蹤劑。常用的示蹤劑包括KCl 和高錳酸鉀溶液，加入的方法有脈沖式加入或階躍式加入。考慮到試驗條件，本試驗采用從鋼包底吹氣體上方區域脈沖加入KCl 示蹤劑的方法。在鋼包底部角部區域設置監測點，檢測流體電導率隨時間的變化趨勢，當示蹤劑濃度變化曲線波動值低于5%時則視為完全均混，如圖1所示，記錄tmix為均混時間［6］。

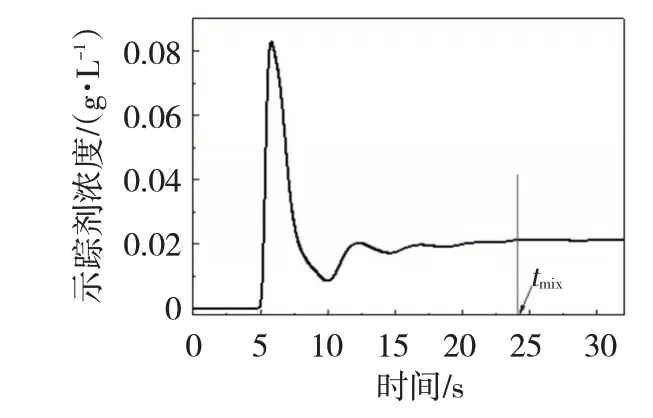
圖1 鋼包監測點示蹤劑濃度隨時間的變化曲線

2.3 物理模型的建立

按照相似比1∶3設計鋼包物理模型，設計圖如圖2所示。采用有機玻璃制成的鋼包模型，鋼包支架由鋁型材加工而成，為鋼包模擬系統設計單獨的供水管路。目前，鋼包模型已經具備上述研究內容的試驗條件。

圖2 鋼包模型設計

2.4 鋼包流體流動及均混行為試驗研究

鋼包底吹條件對于精煉過程具有重要影響，本試驗重點研究單孔噴吹和雙孔噴吹條件下鋼包流體流動特征及均混行為。底吹元件布置位置和試驗方案如圖3和表2所示。以鋼包出口所在的直徑為對稱軸，兩側分別在半徑為226 mm和339 mm的圓周上布置底吹噴嘴。對于底部單噴，考慮到對稱性，分別研究原 1#、12#、15#和 2#四個位置的底吹情況；對于雙噴，分別研究原1#+2#、原1#+4#、12#+2#和12#+4#四種方案。底吹總氣量分別為2 L/min、3 L/min和4 L/min。

圖3 鋼包底吹元件布置位置

表2 鋼包底吹實驗方案

不同單噴條件下的電導率變化曲線如圖4 所示，將濃度變化波動＜5%時刻定義為均混時間。在單孔噴吹條件下，吹氣位置逐漸向鋼包底部中心靠近，均混時間逐漸縮短，并且當采用底部中心單孔噴吹時，均混時間最短，約為105 s。均混時間的變化與吹氣鋼包內的流場密切相關，在中心底部條件下，鋼包內呈現對稱的流動分布特征，最有利于電解質溶液的擴散。

圖4 單噴條件下電解質溶液的電導率變化曲線

不同雙噴組合條件下鋼包內電解質溶液的電導率變化曲線如圖5 所示。重點變換12#和原1#位置分別與2#和4#的組合方式，該組合方式的現場干涉最小。通過比較可以看出，將原1#位置向底部中心移動至12#位置處，并且選擇與之呈135°分布的4#位置相組合，其對應的均混時間最短，約為75 s，比最佳的單噴15#位置均混時間還要短。此外，原1#與2#的組合方式對應的均勻時間僅次于最佳方案，其為120 s。所以，采用雙噴的底吹方式更加有利于發揮鋼包的精煉功能。

圖5 雙噴條件下電解質溶液的電導率變化曲線

圖6和圖7為原1#+2#和原1#+4#底吹條件下，不同吹氣量所對應的均混時間曲線，對于原1#+4#組合，隨著底吹氣量的增加，均混時間逐漸縮短；而原1#+2#組合方式則在中間氣量時達到最短均混時間。

圖6 不同底吹氣量條件下電解質溶液的電導率變化曲線（原1#+2#）

圖7 不同底吹氣量條件下電解質溶液的電導率變化曲線（原1#+4#）

3 數值模擬試驗研究

3.1 數學模型的建立

3.1.1 模型假設及控制方程

本數學模型主要基于如下假設：1）鋼液和底吹氣體均為不可壓縮流體，整體流動為湍流流動。2）忽略流體溫度梯度對流場的影響，假設整個流場溫度均勻分布。3）忽略底吹氣泡的破裂和聚合現象，假設氣泡直徑恒定。4）忽略頂渣對流體流動狀態的影響，自由液面處理為氣液兩相交界面。5）假設反應器出口截面恒定，出口流量恒定。

鋼包底吹氬過程數值模擬均采用歐拉兩相流模型描述反應器內的氣液兩相流動行為。鋼液和氬氣視為相互貫穿的連續介質，對每一相均認為是三維穩定的湍流流動，分別建立各相的連續性方程、動量方程，采用標準k-ε 雙方程模型求解有效黏度。氣液相之間通過曳力、升力、虛擬質量力進行傳遞［7-10］。鋼包內鋼液和氣相流動的方程如下。

1）連續性方程：

式中：下標l和g為液相和氣相；α表示相體積分數；u為速度，m/s；ρ為相密度，kg/m3。

2）動量傳輸方程：

式中：i和j為 1，2，3 分別代表x，y，z三個坐標軸方向。Kg1和k1g為相間動量交換系數，定義為：

式中：f為曳力函數，對于不同的交換系數函數定義有所不同。τg為顆粒弛豫時間，定義為：

本計算中采用Schiller和Naumann曳力模型：

式中：CD為曳力系數。取值為：

其中Re為相對Reynolds準數，定義為：

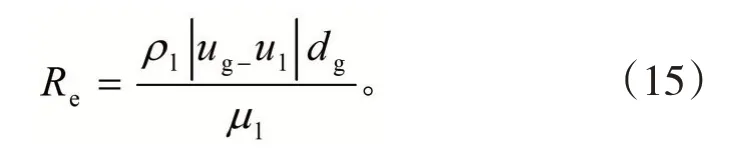
式中：Flj和Fgj為氣液兩相間的非曳力（且Flj=-Fgj），包括升力Flift和虛擬質量力Fvm，即Flj=Flift+Fvm。其中，Flift=-0.5ρlαg（u1-ug）×（▽×ul）。

氣相和液相的升力之間互為相互作用力，即：

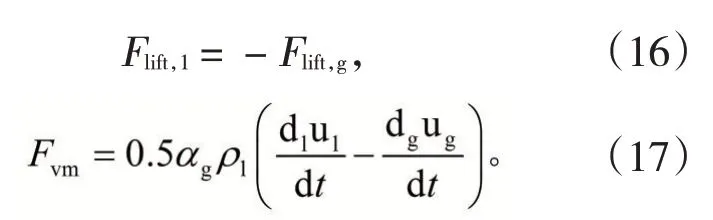
氣相和液相間的虛擬質量力為相互作用力，即：

湍流黏度μt定義為：

3）湍流傳輸方程。吹氬過程中，氬氣的密度和體積分率要遠小于鋼液，因此本計算選用液相的kε湍流模型求解湍動能及其耗散率。

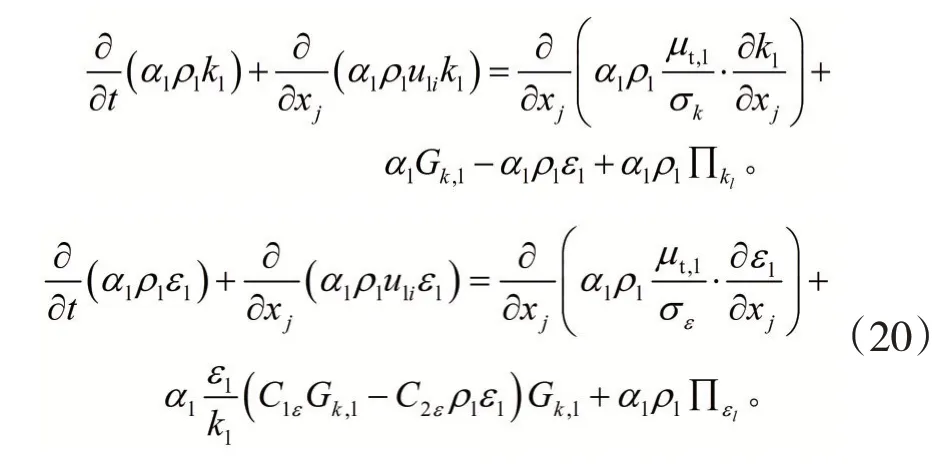
式中：Πkl和Πεl為氣相對液相的作用；Gk，1為湍動能的源項，。

以上方程中的各經驗常數采用Launder 和Spalding 的 推 薦 值 ，Cμ0.09，C1ε1.44，C2ε1.92，Ck1.00，Cε1.30。

3.1.2 模型的邊界條件及初始條件

1）邊界條件設置。a 氬氣入口：鋼包底吹氬氣入口設為質量流量入口，氬氣的質量流量按照體積流量換算。對于不可壓縮流體而言，指定質量流量入口相當于速度入口，根據入口截面積就可將質量流量換算成入口速度。該邊界流速和湍動能及耗散率的數學表達式如下：

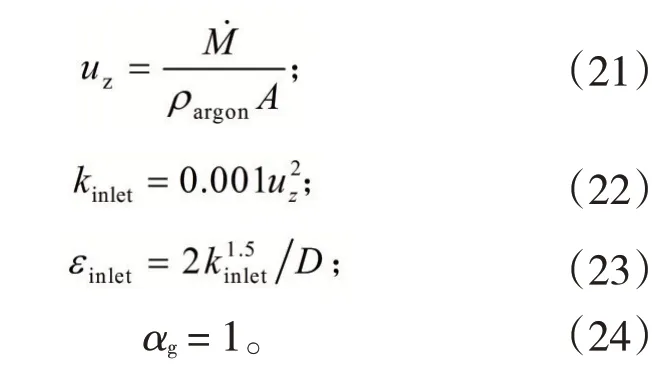
式中：uz為根據質量流量換算得到的入口氣體流速，m3/h；ρargon為氬氣密度，kg/m3；A為吹氣孔橫截面積，m2；Kinlet為入口處的湍動能，m2/s2；εinlet 為入口處的湍動能耗散率，m2/s3；D為吹氣孔直徑，m；αg為氣相體積分率。

b 自由液面：自由液面為Degassing 邊界，該邊界只允許氣相逸出，不允許液相通過該邊界。氣相如何通過該邊界取決于局部的氣體壓力，邊界條件的數學表達式如下：

式中：ux，uy，uz為流體在x，y，z方向上的速度矢量；α為計算單元格內各相所占的體積分率；下標l 和g為液相和氣相。

c鋼包出口：穩定過程底吹氣時，反應器內流體總量恒定，不存在出口邊界問題。研究非穩態澆注時，隨著澆鑄過程的進行，自由液面不斷下降，鋼液的靜壓力逐漸減小，同時為了保證長水口鋼液流量的穩定，需要逐漸增大滑動式水口的開口度，此時流經長水口鋼液的流速也會降低。但本數值計算忽略了鋼液靜壓力的變化對出口流速的影響，因此出口橫斷面尺寸設為恒定值，計算中出口鋼液流量不變，該穩定流量根據對應連鑄系統生產的鑄坯斷面尺寸和拉速確定。d 壁面：鋼包壁面設為無滑移邊界，即各變量在壁面處的值為零。近壁面附近采用標準壁面函數處理。

2）初始條件設置。鋼包澆鑄屬于多相流非穩態流動過程，需要在迭代計算之初設置初始條件。本計算忽略鋼包精煉后期吹氣攪拌結束后鋼包內流體的慣性流動，假設經過一定時間的靜置之后鋼包內流體流動速度為零；因此，本計算初始時刻鋼包內流體整體速度為零。初始時刻由于尚沒有氣體吹入熔池，所以整個熔池充滿了鋼液相，只是在熔池上方存在一定厚度的氣相層。

3.2 數值模擬結果分析

采用數值模擬方式研究了現場雙噴條件下的流場，圖8 為現用鋼包的底吹位置及含氣率模型，圖9為含氣率及密度分布云圖。可以看出，不同含氣率引起截面上的密度分布差異，依靠密度差產生浮力，進而驅動鋼液流動。

圖10和圖11分別為兩噴嘴截面上的速度分布和鋼包內部整體的速度分布。可以看出，底吹噴嘴上方流體的流速最大，在噴嘴所在的縱向截面上形成了非對稱的回環流動，正是該回環流促進了鋼液在鋼包內的均勻行為。從鋼包頂部的速度分布看，兩個噴嘴所形成的回環流動在其中間區域交匯，促使各自的流動轉向，形成了大致垂直于兩噴嘴連線方向的流動，該流股達到包壁后轉為向下的流動，最終加速了鋼液在鋼包內部的流動和均勻行為。

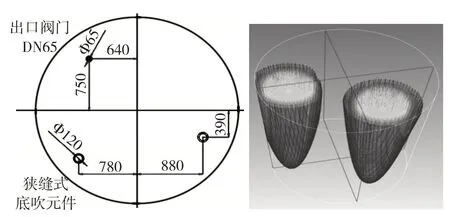
圖8 現用鋼包的底吹位置及含氣率模型

圖9 含氣率及密度分布云圖

圖10 兩底吹位置所在截面上的速度分布

圖11 鋼包內部及頂面的速度分布

4 結 論

4.1 不同含氣率引起截面上的密度分布差異，依靠密度差產生浮力，進而驅動鋼液流動。

4.2 單吹條件下，均混時間的變化與吹氣鋼包內的流場密切相關，采用雙噴的底吹方式更加有利于發揮鋼包的精煉功能。