形象化教學基礎課程探討研究
宋娟
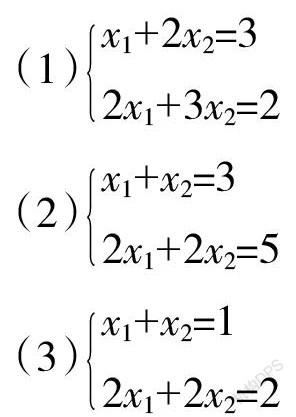
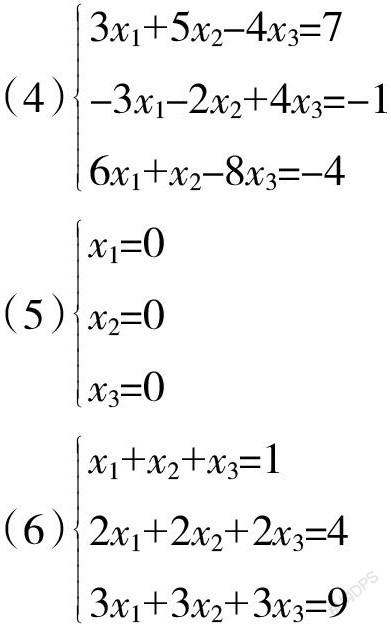



[摘 要] “線性代數”是大學階段理工科專業學生重要的基礎課程之一,具有概念抽象、學生難學、教師難教、應用廣泛等特點。針對此,從直觀的幾何角度通過對線性代數中線性方程組概念的形象化教學,幫助學生將抽象的概念形象化。基于線性代數中概念的應用舉例激發學生學習線性代數的內驅力。最后,結合線性代數的國內教材及國際教材教學對比分析情況,提出了通過調整“線性代數”的考核方式來適應線性代數現代化教學需求的方案。
[關鍵詞] 線性代數; 線性方程組;形象化教學;應用舉例;考核方式
[基金項目] 2019年度江南大學教改項目“全英文大學數學課程研究與建設”(JG2019096)
[作者簡介] 宋 娟(1982—),女,江蘇宿遷人,博士,江南大學理學院講師,主要從事計算數學研究。
[中圖分類號] G642? ?[文獻標識碼] A? ?[文章編號] 1674-9324(2021)47-0091-04? ? [收稿日期] 2021-05-06
一、引言
“線性代數”是大學階段理工科、經濟、管理等專業必修的一門重要的數學基礎課程,對學生數學思維能力的培養、后期專業課程的學習、編程能力的培養、解決問題及創新實踐能力的培養具有重要的作用[1,2]。但是,據調研,學生對“線性代數”的學習往往停留在記概念、記定理,甚至做題思路都是死記硬背的層面,對其中的概念等理論知識往往不能真正理解,從而不能真正體會“線性代數”的意義。因此,課程學完后往往不能應用線性代數去解決實際問題。
事實上,“線性代數”中很多概念具有深遠的意義,且“線性代數”在諸多領域如計算機圖形學、預測及優化中均有廣泛的應用。那么,如何把抽象的線性代數,以形象、易懂的方式呈現給學生,并用有趣的例子展示線性代數的廣泛應用,激發學生學習線性代數的主觀能動性,是我們應該深刻思考的問題。
下面結合筆者的教學經驗,舉例闡述線性代數概念的形象化教學,基于線性代數的應用舉例來激發學生學習線性代數的內在動力。通過線性代數的國內國際教材對比分析,及國內的教學環境分析,認為通過適當調整“線性代數”的考核方式可以有效適應線性代數的現代化教學需求。
二、線性方程組解的概念的形象化教學
線性方程組的解是線性代數的主線,也是線性代數的重點和難點內容,在科學、工程和生活中均具有廣泛的應用。針對此,本文以線性方程組的解為例,從幾何的角度對這個概念進行形象化闡述,幫助學生更好地掌握這個概念,為學生以后利用這個知識點解決問題奠定一定的基礎。
線性方程組的解,從幾何圖形上看,可以看成線性方程組中各個方程所對應的圖形的交集。下面,分別以包含兩和三個未知變量的線性方程組為例進行說明,含有多個未知變量的多元線性方程組可以在此基礎上進行自然的推廣。下面首先以三個二元線性方程組為例進行說明。
二元一次方程表示一條直線。很顯然,方程組(1)中兩個方程所對應的直線的斜率不同,所以是兩條相交的直線,兩相交直線的交集為其交點,此時,交點為方程組的唯一解;方程組(2)中兩個方程對應的直線的斜率相同,但截距不同,所以是兩條平行的直線,兩平行直線無交集,此時,方程組無解;方程組(3)中兩個方程對應的直線的斜率相同,截距相同,是兩條重合的直線,兩重合直線的交集為這條直線上所有點,此時,方程組有無窮多解,即為直線上所有的點。
把上面的幾何語言引入矩陣的秩進行重新闡述,即為線性方程組解的判定定理。再以三元線性方程組為例進行說明。
由空間解析幾何知,對于方程組(4),第一個方程表示法向量為n1=(3,5,-4)的平面,第二個方程表示法向量為n2=(-3,-2,4)的平面,第三個方程表示法向量為n3=(6,1,-8)的平面,三個平面的法向量既不平行,也不垂直,是三個兩兩相交且不垂直的平面。因第一個平面和第二個平面的交線L的方向向量為n1×n2=(12,0,9),第二個平面和第三個平面交線M的方向向量為n2×n3=(12,0,9),第一個平面和第三個平面交線K的方向向量為n1×n3=(12,0,9),很顯然,直線L、M與K的方向向量相同,且直線L、M和K均過點(1/3,2,1),因此三個平面的交集為直線L,直線L上所有點為第一個方程組的解。此時,方程組有無窮多解。
對于方程組(5),三個方程表示三維空間直角坐標系中相互垂直的三個平面,原點為唯一交點,此時,原點為方程組唯一解。
對于方程組(6),三個平面的法向量互相平行,且第一個方程過(0,0,1)點,不在第二個方程和第三個方程確定的平面上,第二個方程過(0,0,2)點,不在第一個方程和第三個方程確定的平面上,第三個方程過(0,0,3)點,不在第一個方程和第二個方程確定的平面上。因此,三個方程所確定的三個平面是互相平行且不重合的,此時,方程組無解。
類似地,對于包含三個未知數的方程組的解,在引入矩陣的秩后,可以將上面的幾何語言采用系數矩陣的秩和增廣矩陣的秩的關系重新闡述為線性方程組解的判定定理。
三、“線性代數”應用舉例
為了進一步激發學生學習“線性代數”的興趣,讓學生感受線性代數是因用而學,且學習的目的是學以致用,下面以“線性代數”在計算機圖形學以及未來預測中的應用為例進行闡述。
(一)計算機圖形學中的應用:物體的投影
三維物體在二維計算機屏幕上的顯示方法就是把它投影到一個可視平面上。三維物體和二維物體若僅考慮其形狀,則物體上每一點有其對應的坐標(x,y,z),那么它投影到計算機屏幕上的坐標(x*,y*,0)是如何確定的?這個問題可以利用線性代數中的線性變換來實現。
例:設三維空間中一長方體的8個頂點坐標分別為(4,1,6),(5,1,6),(5,0,6),(4,0,6),(4,1,2),(5,1,2),(5,0,2),(4,0,2),求此長方體在投影中心為(0,0,9)的透視投影下的像。
投影坐標可用投影矩陣P及長方體三維坐標對應的齊次坐標構成的矩陣得到。
每一列的前三行除以第四行的對應元素所對應的點即為長方體投影后計算機屏幕上圖形的頂點。上面的這個例子顯示,基于“線性代數”中矩陣的乘法,可以方便確定出空間三維物體在計算機屏幕上的顯示圖形。
(二)未來預測中的應用
因未來預測在生活、商業中具有重要作用,下面我們以線性代數在未來預測中的應用為例。假設A市只有一個機場、市中心和火車站。在A市,出租車公司大約有3000輛汽車,開始分配在機場、市中心和火車站三個點的車輛分別為500、1500、1000。據統計,出租車由機場出租后回到機場、市中心、火車站的概率分別為0.9、0.01、0.09,由市中心出租后回到機場、市中心、火車站的概率分別為0.01、0.9、0.09,由火車站出租后回到機場、市中心、火車站的概率分別為0.09、0.01、0.9。那么,第六天機場、市中心、火車站三個站點分別有多少輛出租車被租出或準備出租?隨著天數的增加,三個地點所需的出租車輛會不會大約固定,若固定,三個站點該如何分配出租車的比例?
顯然,第五天各個站點的車輛分別768、958、1274輛。
即三個站點分配的出租車基本固定,大約為210、450、2340輛。
四、結語
本文以線性方程組的解為例,對“線性代數”中的抽象概念進行其幾何意義下的闡述講解,從而將抽象的線性代數概念形象化,幫助學生進一步理解概念、升華概念,為提高學生的數學素養奠定一定的基礎。為進一步提高學生的學習興趣,促進學生認識到“線性代數”是以需求為牽引,內需為導向,介紹了“線性代數”中的線性變換在計算機圖形學中及在未來預測中的應用,激發了學生學習線性代數的內驅力,進一步培養了學生利用線性代數知識解決問題的能力。
最后,基于中外線性代數教材的比較[1,3]及國內的教學環境分析,筆者認為多元化“線性代數”的考核方式可以有效促進線性代數的教學與國際接軌,適應現代化教學需求。
目前,國內高校“線性代數”考核方式基本是閉卷考試,能較好考查學生掌握教材上基本知識點的情況,也能有效促進學生在較短時間內掌握用途較多的“線性代數”這門課的基本知識點。但是,目前國內的教材關于一些概念的背景及應用與國外的教材相比,還是相對較少的。
為了彌補這方面的不足,可以考慮將“線性代數”的考核按比例分為閉卷和開卷兩部分。閉卷部分就是我們目前的考試方式,占考核的主要比例。開卷部分可以設為類似于國外線性代數教材中的應用性問題的考核,考查學生運用所學知識解決實際問題的能力,以考促學,考學相長,提高學生解決問題的能力及學生綜合數學素養,以適應現代化的線性代數教學需求。
參考文獻
[1]David C. Lay, Steven R. Lay, Judi J. McDonald. Linear Algebra and Its Applications (Fifth Edition)[M].劉深泉,張萬芹,陳玉珍,等譯.北京:機械工業出版社,2018.
[2]同濟大學數學系.工程數學線性代數[M].6版.北京:高等教育出版社,2014.
[3]王正盛.中外線性代數教材的比較與探討[J].大學數學,2009,25(1):200-203.

