近十年上海蔬菜價格的SARIMA 分析與預測

鄭秀國,楊 娟,錢婷婷,許葉穎

(上海市農業科學院農業科技信息研究所,上海數字農業工程技術研究中心,上海201403)

蔬菜是“菜籃子工程”的主要產品之一,蔬菜產業也是城市近郊農業生產者的重要經濟來源。 然而,蔬菜價格不僅受到市場供求、自然氣候、生產成本、市場流通等規律性因素的影響,還會受到突發的氣候變化、供求變化等影響,尤其是近年來大市場大流通下蔬菜供應的季節性或種類性不均衡時有發生,導致蔬菜價格波動頻繁。

作為生物性產品,蔬菜的供應受季節氣候的影響最大,其價格隨著供應的周期性波動而波動,在時間序列上表現出明顯的季節性和周期性特征,時間序列模型可較好地反映這種變化特征。 常用于農產品價格分析的時間序列模型有自回歸移動平均模型(ARIMA 模型)、季節自回歸移動平均模型(SARIMA 模型)和Holt-Winters 指數平滑模型(Holt-Winters 模型)等,其中SARIMA 模型、Holt-Winters 模型均考慮到季節性因素的影響[1]。 SARIMA 模型在農產品價格分析預測中應用十分廣泛,如陳燦煌等[2]、陳兆榮等[3]運用該模型預測了中國農產品價格指數,王云鵬[4]用其預測農業生產資料價格指數。 應用該模型預測農產品價格、蔬菜價格和單種類蔬菜價格也都取得了較好的效果[5-7],也是雞蛋價格、肉雞價格、生豬價格、豬肉價格常用的分析預測方法[8-11]。 李干瓊等[12]采用5 種短期預測模型預測2009 年西紅柿價格,表明SARIMA 模型明顯優于其他4 種模型。 王美鳳等[13]對4 種上海青菜價格預測模型進行了比較研究,表明SARIMA 模型的預測效果最好。 蔬菜價格是同期多種單種類菜價的匯總,開展蔬菜價格波動特征分析和預測研究,可為管理部門的政策調控和生產者的經營決策提供參考,對于減少蔬菜價格大幅波動對市民生活和蔬菜生產者的影響具有重要意義,然而尚未見蔬菜總體價格的波動特征與預測分析研究的報道。 為此,本研究采用2010 年1 月—2019 年12 月上海蔬菜批發價數據,建立上海蔬菜SARIMA 模型,進而對2020 年1—6 月上海蔬菜價格進行預測,通過模型預測效果分析進一步驗證模型效果,最后根據SARIMA 模型參數值分析上海蔬菜價格波動特征。

1 數據來源與模型方法

1.1 數據來源

本研究所使用的數據序列為2010 年1 月至2020 年6 月上海蔬菜批發市場平均價格(元人民幣∕kg,下同),記為PR,來源于上海市農產品價格監測與分析預測系統。 其中2010 年1 月—2019 年12 月數據用于上海蔬菜SARIMA 模型建立,2020 年1—6 月數據用于進一步驗證分析模型預測效果。

1.2 建模方法

SARIMA(p,d,q)(P,D,Q)模型結構中,p 為自回歸項數,q 為移動平均項數,d 為差分次數,P 是季節自回歸階數,Q 是季節移動平均階數,D 為季節差分次數。 具有季節性、趨勢性和周期性的平穩數據序列{Bt,t=1,2,…},可以采用SARIMA(p,d,q)(P,D,Q)模型結構建立模型。

首先對上海蔬菜批發價數據序列進行季節性、趨勢性檢驗。 季節性檢驗通常采用時間序列趨勢圖來判斷,若趨勢圖是以年為周期變動,則時間序列具有季節變動特征。 趨勢性檢驗是采用CensusX-12 乘法方法對數據序列進行季節調整分解,獲得季節調整后的趨勢循環序列,再運用H-P 濾波法對獲得的趨勢循環序列進行趨勢波動與循環波動序列分離,分離出的趨勢波動圖可觀察出序列的變化趨勢。

SARIMA 模型的建立與應用可通過Eviews 軟件實現,主要過程如下:

1)序列平穩性檢驗。 可通過ADF 單位根檢驗來判斷,對于非平穩時間序列,可以通過數據變換和差分實現序列的平穩化,并采用時間序列的自相關函數(ACF)和偏相關函數(PACF)是否截尾來判定序列的平穩性。

2)模型的識別。 主要通過觀察序列的自相關函數(ACF)和偏相關函數(PACF)對可能的p,d,q 和P,D,Q 的參數值進行估計,由此構成不同的SARIMA 模型結構形式。

3)模型的參數估計。 運用最小二乘法估計模型的系數,并對其顯著性進行檢驗。 對于不同參數模型的選優可采用BIC(貝葉斯信息)準則等綜合判斷。 最后,對選出的模型檢驗其殘差是否為白噪聲,一個適合的模型的殘差序列應是白噪聲過程,其ACF 和PACF 不應與0 有顯著性差異。

4)模型預測。 由上述過程確定模型的最終參數后,即可得到模型,使用模型進行預測。

2 結果與分析

2.1 序列平穩化

從圖1 可以看出,上海蔬菜價格表現出較明顯的季節性,每年3 月至次年3 月蔬菜價格呈“W”型波動規律,價格高點多出現在3 月和9 月,價格低點多出現在6 月和11 月,數據在周期內呈現整體遞增趨勢,為非平穩序列。

首先,為消除序列可能存在的異方差,將原始序列進行對數化處理;其次,為消除趨勢性,對原始序列進行季節性差分和普通一階差分。 由圖2 可以看出,處理后序列ΔΔ12LnPR 的自相關函數ACF 和偏相關函數PACF 整體呈現截尾態勢,由此認為ΔΔ12LnPR 是平穩的序列。

2.2 模型建立與參數識別

本研究選擇多種不同的模型進行擬合,如SARIMA(0,1,1) ×(1,1,1)12、SARIMA(2,1,1) ×(1,1,1)12、SARIMA(2,1,1) ×(1,1,2)12、SARIMA(2,1,2) ×(2,1,1)12、SARIMA(2,1,2) ×(2,1,2)12等p、q 和P、Q為3 以內的各種取值組合,發現SARIMA(3,1,3) ×(2,1,0)12參數顯著性t檢驗結果最好。 從表1 可以看出,該模型結構各參數的相伴概率均小于0.15,確定上海蔬菜模型結構為SARIMA(3,1,3) ×(2,1,0)12。模型結構為:(1 -φ1B-φ2B-φ3B)(1 -Φ1B12-Φ1B24)Δ1Δ112logPr=(1 -θ1B-θ2B-θ3B)εtεt-N(0,0.100)。

回歸方程的決定系統為0.71,誤差項的方差估計值為0.100,模型中各參數的取值見表1。 模型的殘差序列經檢驗為平穩的白噪聲序列。

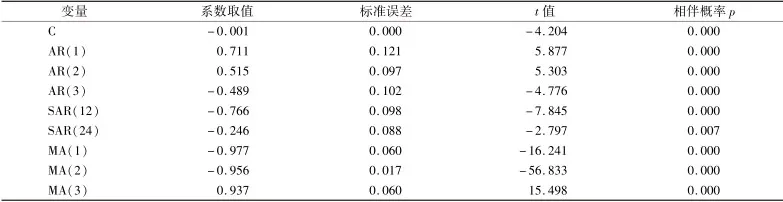
表1 SARIMA 模型參數估計與相關檢驗結果Table 1 Model parameter estimation and test results based on SARIMA model

2.3 模型預測

根據建立的SARIMA(3,1,3) ×(2,1,0)12模型對2020 年1—6 月的上海蔬菜價格進行靜態預測和動態預測,通過實際價格和預測價格的比較,判斷模型的預測精度。

市場調查發現,假期對蔬菜價格有一定影響,進一步分析了春節假期對蔬菜價格的影響。 從2010—2019 年上海蔬菜價格數據來看,含春節期間價格的1 月蔬菜月平均價格比不含春節期間價格的1 月上海蔬菜月平均價格低2.0%,含春節期間價格的2 月蔬菜月平均價格比剔除春節期間價格的2 月上海蔬菜月平均價格高12.3%,可見,春節假期對蔬菜價格影響效果不定。 但是春節當月的蔬菜價格整體高于其前后月份,如春節在1 月,1 月蔬菜價格比其前一個月和后一個月的價格平均高2.9%;春節在2 月,2 月蔬菜價格比其前一個月和后一個月的價格平均高7.7%。

為此,本研究在進行預測時考慮了假期效應,如果春節所在月份預測值高于前一個月預測值和后一個月預測值的平均值歷史水平則不進行春節調整,反之則對春節所在月份的預測值進行相應調整——若春節在1 月,則1 月下調2.0%;若春節在2 月,則2 月上調12.3%。 如表2 所示,靜態預測結果的平均誤差為7.3%,動態預測結果的平均誤差率為4.6%,上海蔬菜價格預測數據與實際數據基本一致。

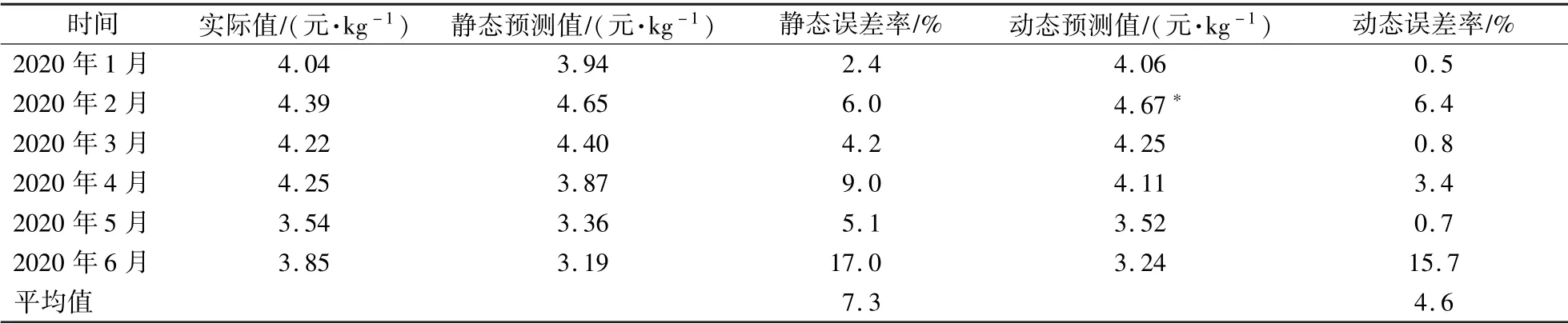
表2 上海蔬菜價格靜態預測結果和動態預測結果Table 2 Static and dynamic prediction results of vegetable price in Shanghai

3 結論與討論

研究結果表明,上海蔬菜價格具有較為明顯的季節性和周期性特征,可用SARIMA 模型對上海蔬菜價格進行分析和預測。 根據模型的顯著性檢驗和模型參數的顯著性檢驗結果,SARIMA(3,1,3) ×(2,1,0)12模型效果最佳。 從模型參數值可以看出,上海蔬菜價格為非平穩序列,一階差分序列為平穩序列;根據參數取值,可看出上海當月蔬菜價格不僅與其前3 個月的價格密切相關,而且受前2 年同月價格的影響。

上海蔬菜價格SARIMA(3,1,3) ×(2,1,0)12模型預測的上海蔬菜2020 年1—6 月批發價(經春節調整后)與實際價格的對比分析結果表明,模型靜態預測的平均誤差為7.3%,動態預測的平均誤差為4.6%,實際應用中可結合2 種預測方式,達到更好的預測效果。 SARIMA(3,1,3) ×(2,1,0)12模型能較好地表現上海蔬菜價格的波動特征,可用于分析和預測上海蔬菜價格未來走勢,指導產業發展。 但還要注意,時間序列模型建模主要依據歷史價格所包含的信息,而實際影響市場價格波動的還有一些突發性因素,如臺風暴雨、低溫、暖冬等惡劣天氣或者交通、疫情等突發事件,所以在實際價格的走勢分析預測中,可在模型分析預測出規律性影響因素結果的基礎上,再疊加考慮這些突發因素的影響,從而科學判斷出各種影響因素對蔬菜價格影響的程度。