機體彈性對某型民機起落架著陸載荷影響分析

徐 堯，周文博

(上海飛機設計研究院，上海 200232)

大型民用飛機著陸過程中起落架撞擊地面產生的起落架載荷是起落架的設計載荷之一，著陸瞬間的機體響應載荷構成飛機結構的設計載荷。大展弦比飛機機體結構柔性較大，在著陸過程中機體彈性對起落架減震器的影響較大，著陸分析中需要考慮彈性機體對著陸能量的耗散作用[1-4]。研究機體主要彈性模態(tài)對起落架著陸載荷的影響，有助于理解飛機結構與起落架嚴重載荷的關系，進而利于飛機機體與起落架一體化設計。

目前，國內外對于機體彈性對起落架著陸性能影響有一些研究并且取得一定的進展，但較多的是從理論上分析機體前幾階等效固有頻率對起落架著陸性能的影響。在仿真分析方面，很多研究將飛機等效為多質量塊系統(tǒng)[5-7]，只能分析較低階次彈性模態(tài)的影響，缺乏工程應用價值。

本文在經過落震試驗驗證的多柔體起落架動力學模型基礎上，進一步考慮機體彈性，將能夠很好地表征機體剛度特性和質量特性的全機梁單元動力學模型導入ADAMS，與多柔體起落架模型連接，得到起落架與機體多柔體系統(tǒng)動力學全機模型，該模型能夠全面考慮起落架彈性和機體各個階次彈性模態(tài)對著陸性能的影響，同時能夠考慮機體彈性模態(tài)的模態(tài)阻尼比對著陸載荷的影響，具有較高的工程實用價值。

1 多柔體系統(tǒng)動力學計算原理

多柔體系統(tǒng)是指由多個剛性體或柔性體通過某種形式連接的復雜機械系統(tǒng)，柔性體使用離散化的若干個單元的有限多個節(jié)點自由度來表示物體無限多個自由度，單元節(jié)點的彈性變形可以近似地用少量模態(tài)線性組合來表示。

如果物體在某坐標系的位置用它在慣性參考系中的笛卡爾坐標x=(x,y,z)和反映剛體位置的歐拉角ψ=(ψ,θ,φ)來表示，模態(tài)坐標用q=[q1,q2,…,qm]T表示，其中q1,q2,…,qm是Craig-Bamptom模態(tài)坐標[8-9]，m表示模態(tài)階數(shù)，則柔性體的廣義坐標ξ表示為：

ξ=[x,ψ,q]T=[x,y,z,ψ,θ,φ,qj]T(j=1,2,…,m)

(1)

通過拉格朗日乘子法建立柔性多體運動微分方程[10-11]：

(2)

式中：M為柔性體的質量矩陣；Φ為約束方程；K，D分別為模態(tài)剛度矩陣和模態(tài)阻尼矩陣；Kξ，Dξ分別代表物體內部由于彈性變形和阻尼引起的廣義力；fg為廣義重力；λ為對應約束的拉格朗日乘子；Q為對應于外力的廣義力。

2 多柔體系統(tǒng)全機動力學仿真模型

首先建立起落架多柔體系統(tǒng)動力學模型，如圖1所示。模型考慮了起落架結構的彈性、緩沖支柱緩沖特性、輪胎動態(tài)壓縮特性以及結構之間的運動約束關系，起落架各結構部件均處理為柔性體，在仿真分析中考慮了起落架的變形，起落架多柔體系統(tǒng)模型的動力學特性經過落震試驗數(shù)據的驗證。

圖1 起落架多柔體系統(tǒng)動力學模型

為表征飛機全機動力學特性，民用飛機機體各部件包括機身、機翼和尾翼等常常被簡化為梁單元，部件梁單元的位置為飛機各部件剛性軸位置，剛性軸為每個框或肋截面剛心的擬合線，飛機剛性軸示意圖如圖2所示。梁單元模型在機身框和翼面肋的位置劃分節(jié)點，每個梁單元剛度根據飛機詳細有限元模型計算得到；全機的質量離散化為若干集中質量，掛載在梁單元的節(jié)點上；機翼與機身、平尾垂尾與機身使用RBE2剛性單元進行連接；為了便于機體與起落架的連接，在起落架連接鉸點位置劃分節(jié)點，再使用RBE2剛性單元連接至相關站位。建立的梁單元模型較為簡化但能夠很好地表征全機的動力學特性，機體梁單元模型經過全機地面共振試驗(GVT)的修正，保證動力學特性與真實飛機一致。梁單元機體有限元模型通過NASTRAN SOL103模態(tài)分析生成MNF模態(tài)中性文件，將模態(tài)中性文件導入ADAMS表征柔性機體。

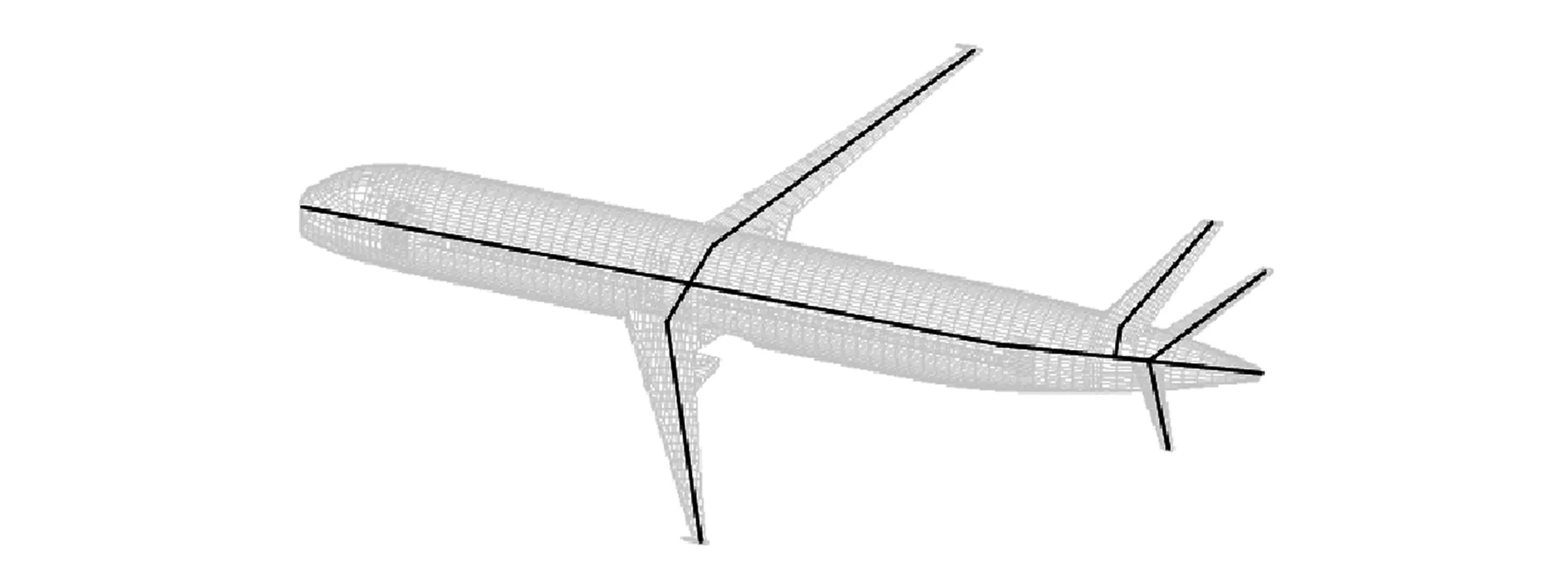
圖2 飛機剛性軸示意圖

在ADAMS中將柔性機體模型與起落架多體動力學模型連接，連接采用襯套(BUSHING)單元實現(xiàn)。完成連接后的柔性機體與起落架一體化模型如圖3所示。

圖3 柔性機體與起落架一體化模型

3 考慮機體彈性全機著陸仿真分析

一體化全機模型能夠設置全機俯仰著陸角度、全機向前速度及下沉速度，通過仿真分析可以得到著陸時刻起落架撞擊地面引起的輪胎載荷、輪軸點載荷、起落架鉸點載荷以及機體各處的內力響應載荷。飛機著陸過程往往關注輪軸點垂向和航向載荷，本文以輪軸點載荷為例，研究柔性機體對著陸過程輪軸點載荷的影響。

在考慮機體彈性模態(tài)時，設置機體模態(tài)阻尼比。在模態(tài)坐標系下，模態(tài)阻尼比為模態(tài)阻尼與臨界阻尼之比。在定義模態(tài)阻尼比之后，計算每一階模態(tài)阻尼系數(shù)得到的對角陣即為模態(tài)阻尼矩陣D，本文根據行業(yè)經驗定義每一階模態(tài)阻尼比為3%。

對全機一體化模型進行著陸仿真分析，分析中假定著陸時刻飛機受到的升力等于重力，飛機以一定的下沉速度和向前速度著陸，分析輪胎接地后0.5 s內的輪軸點載荷，輪胎接地時刻為0.1 s。首先考慮柔性機體包括剛體模態(tài)在內的前70階模態(tài)，頻率范圍為0 ～100 Hz，忽略更高頻率的影響，得到考慮機體彈性的起落架輪軸點載荷；再將機體處理為剛性體，即僅考慮機體的6個剛性模態(tài)，得到剛性機體起落架輪軸點載荷。對比兩組情況下的前起落架和主起落架載荷，如圖4和圖5所示，對圖中載荷數(shù)值做歸一化處理。兩圖中較高較平緩的曲線為垂向載荷曲線，較低且有振蕩的曲線為航向載荷曲線，航向載荷的第一個峰值由著陸瞬間輪胎起旋作用引起，隨后的振蕩的原因是起落架具有前后方向剛度。

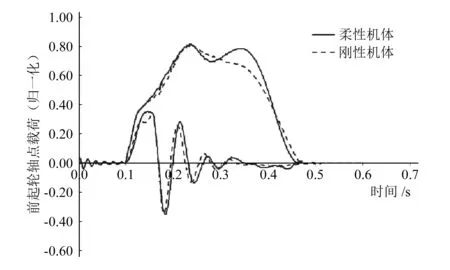
圖4 剛/柔機體前起落架載荷對比

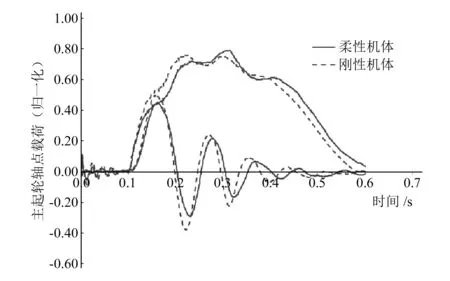
圖5 剛/柔機體主起落架載荷對比

從圖4可以看出，考慮機體彈性后，前起落架輪軸點垂向載荷由一個峰值變?yōu)閮蓚€峰值，航向載荷變化不顯著；從圖5可以看出，考慮機體彈性后，主起落架輪軸點垂向載荷峰值時間發(fā)生推遲，航向載荷峰值變小。

由圖可知，彈性機體對著陸起落架載荷影響較為顯著，忽略機體彈性會帶來較明顯的誤差。為進一步研究機體的彈性模態(tài)對載荷的影響，在計算中逐階加入機體的彈性模態(tài)，定性分析每階彈性模態(tài)對起落架載荷的影響，表1列出了機體各階模態(tài)及對應的振型。

表1 機體模態(tài)

模態(tài)階次對前起載荷和主起載荷的影響如圖6和圖7所示。在分析中依次增加機體彈性模態(tài)的數(shù)量，發(fā)現(xiàn)與考慮第1～13階模態(tài)的起落架載荷曲線相比，考慮第1～14階模態(tài)后起落架載荷曲線發(fā)生較顯著變化，且比較接近柔性機體載荷結果，說明了第14階以后的機體模態(tài)對起落架載荷影響不明顯。

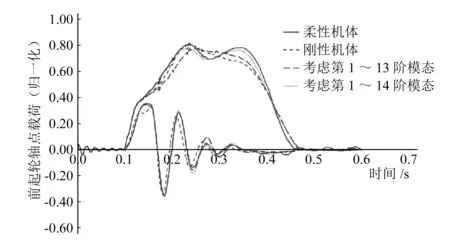
圖6 模態(tài)階次對前起載荷影響

圖7 模態(tài)階次對主起載荷影響

通過上述分析可知，機體低階模態(tài)(10 Hz以內)對起落架載荷的影響占主要作用，在低階模態(tài)中機身垂向一階彎曲模態(tài)影響最為顯著。機身垂向一階彎曲模態(tài)的振型如圖8所示，由圖可知，機身在前起落架和主起落架位置處的模態(tài)變形較大，因此這一階模態(tài)對起落架垂向載荷影響較大。

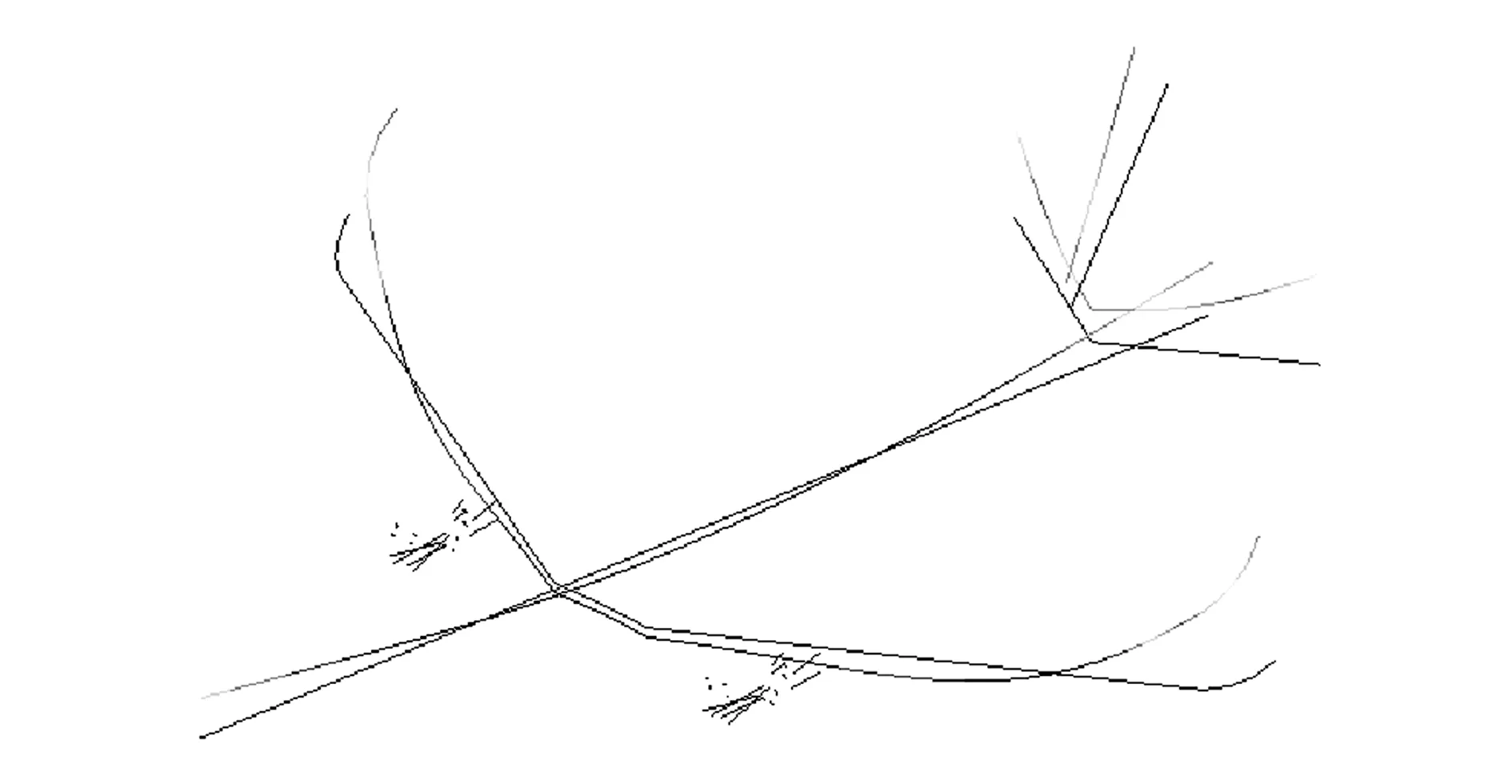
圖8 機身垂向一階彎曲模態(tài)振型圖

一般認為第一階機體彈性模態(tài)，即機翼垂向一階彎曲模態(tài)，對主起落架著陸載荷影響最大，實際上，從圖9可以看出，機翼垂向一階彎曲模態(tài)的模態(tài)變形主要在外翼，而主起落架所在的接近翼根位置處模態(tài)變形并不大，在圖6和圖7中，機翼垂向一階彎曲模態(tài)包含在第1～13階模態(tài)中，從曲線對比可見，機翼垂向一階彎曲模態(tài)對起落架著陸載荷的影響較小。

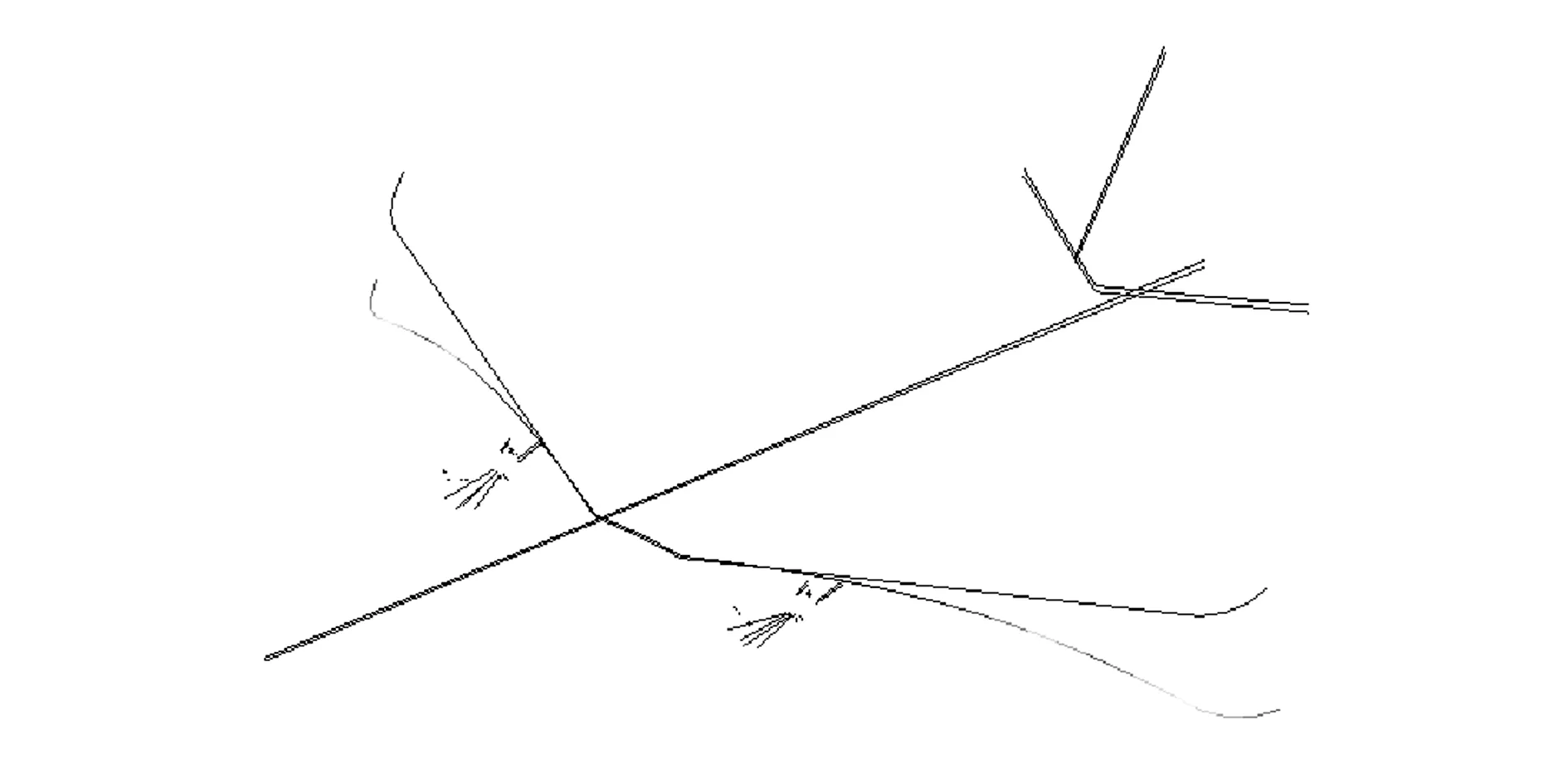
圖9 機翼垂向一階彎曲模態(tài)振型圖

本文的分析基于起落架前三點布局民用飛機，機體的模態(tài)分布及對應的模態(tài)振型也針對此類型飛機。對于此類型飛機，動態(tài)著陸的起落架載荷需要考慮機體的彈性，機體的低階模態(tài)尤其在起落架位置處存在較大模態(tài)變形的模態(tài)，對起落架載荷影響較為顯著。

4 結論

本文建立了柔性機體與起落架彈性耦合的一體化全機模型，應用多柔體模態(tài)綜合方法計算考慮機體彈性的起落架著陸載荷，對比分析了剛性機體起落架著陸載荷與柔性機體起落架著陸載荷，并通過逐階考慮機體彈性模態(tài)的方法定位顯著影響起落架著陸載荷的機體模態(tài)，得到如下結論：

1)機體彈性影響著陸過程中起落架載荷的峰值及趨勢，在分析起落架著陸載荷時需要考慮機體彈性；

2)機體的低階彈性模態(tài)中機身垂向一階彎曲模態(tài)對民用飛機的著陸載荷影響最為顯著，在分析中需要重點關注引起起落架位置模態(tài)變形較大的機體模態(tài)。