如何利用等量關系提高小學生列方程解應用題的能力

葉文婷

【摘?要】由于小學生在四年級前一直用算術方法解決問題，因此，受定向思維影響，解題時思路仍停留在用算術方法解應用題上，所以列方程解應用題成了小學數學教學中的難點。如果要突破這個難關，主要是讓學生準確找出題中的等量關系，從而提高小學生列方程解應用題的能力。

【關鍵詞】小學生;找等量關系;列方程;應用題

列方程解應用題屬于小學階段四至六年級的內容，小學階段主要的解題方法有兩種，一種列算式解答，一種列方程解答。列算式解答與用方程解答，相同點都以常見的數量關系為基礎，再利用四則運算建立與題目相符合的式子;而它們的區別主要是思考方法不同。列算式解決實際問題時，往往是針對未知數，根據題目的思路，用已知量與運算符號把未知數作為最終的“目標”求出來，整個過程考驗學生的思考能力，解題思路也常常不夠直截了當，局限性較大，對于部分學困生來講達不到很好的解題效果。列方程解決實際問題時，以一個字母來表示未知數，結合已知量參與列式計算，相對列算式解答而言更明了，降低了思維難度，適用面廣。那么如何找等量關系并利用等量關系列方程呢？以下便是本人在實際教學中總結的幾點。

一、根據圖形的面積、周長等計算公式確定等量關系列方程

學生在學習幾何圖形時，已經對平面圖形的周長和面積的計算公式以及立體圖形的表面積和體積有了了解，這便有利于他們把等量關系具體化。

例如“一個長方形的棱長總和是84cm，已知長是寬的1.5倍，寬是高的2倍，求這個長方形的長、寬、高分別是多少cm？”

我們可以根據長方體的體積公式得等量關系：長×寬×高=長方體的體積，根據這個等量關系式列出方程：

解：設梯形的高為cm，寬是2cm，長是（2×1.5）cm，根據題意得：

這道題目只要確定數量最小的高作為未知數，再根據長方體的體積公式建立等量關系，做題的思路就會非常清晰，也增強了學生解題的效率。

二、利用具體數量以及其數量關系作為等量關系

常見的數量關系有：單價×數量=總價;速度×時間=路程;工效×時間=工作總量;單產量×數量=總產量等數量關系，我們可以讓學生思考所做的題目屬于什么類型的，再根據這些數量關系直接寫出等量關系，列出方程。

例如：“一輛貨車和一輛客車同時從相距770千米的兩地相對開出，5.5小時后相遇。貨車每小時行60千米，客車每小時行多少千米？”

這是相遇問題的數量關系，每小時行駛的速度和×相遇時間=行駛的總路程，根據這個關系式我們可以列方程：

解：設客車每小時行千米，根據題意得：

三、提取關鍵語句構建等量關系

很多應用題都有體現數量關系的句子，解題時，排除無用的信息，提取關鍵語句，理解相關含義，就能正確找出等量關系。

例如：“張良有7張郵票，哥哥給了他3張后，他的郵票數就是哥哥的2倍，哥哥原來有多少張郵票？”

該題的關鍵句是“哥哥給了他3張后，他的郵票數就是哥哥的2倍。”這時，張良的郵票數是（7+3）張，也就是（哥哥的票數-3）的2倍。那么我們就可以列方程：

解：設哥哥原來有張郵票，根據題意得：

學生在解決應用題時，找到關鍵語句并分析其中的等量關系也是提高學生列方程能力的優化策略之一。

四、用畫線段圖展現等量關系

線段圖能夠使學生把問題中的信息整理后，把抽象的數量關系具體化地呈現出來，既突顯出隱蔽的數量關系，又把復雜的題目更直觀簡單地表示出來。因此，我們可以借助畫線段圖找等量關系。

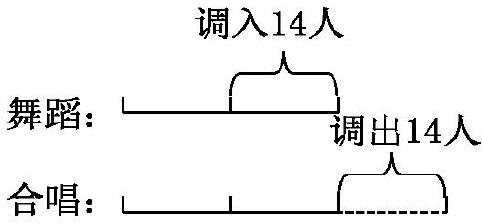
列如：“合唱隊的人數是舞蹈隊的3倍，如果從合唱隊往舞蹈隊調入14人，則兩隊的人數相等，舞蹈隊有多少人？”

根據題意，可以畫出下面的線段圖：

從圖中很容易得出：合唱隊-14=舞蹈隊+14

解：設舞蹈隊有人，根據題意得：

五、運用不變量揭示等量關系

面對正、反比例的應用題，我們可以根據題目的“比值一定”和“積一定”，也就是“不變量”尋找等量關系。

例如：“含鹽量為20%的鹽水200克，再加入多少克水就能使含鹽量降低到16%？”

這題加入水份后水的重量在變，鹽水的重量也在改變，只有鹽的重量是保持不變的，那么我們就要學會抓住這個“不變量”，發現其中的等量關系是：加水后鹽的重量=加水前鹽的重量，列方程解答：

解：設加入克水，根據題意得：

對于此類型的難題，只要抓住“不變量”就能讓學生面對問題時迎刃而解。

六、根據事情發展的順序和實際關系找等量關系

部分實際生活中的數學應用題涉及時間順序的，我們可以以發展的順序為基礎，結合實際關系尋找等量關系列方程。

列如：“一輛公交車上有乘客38人，在火車站有14人下車，同時又上來一些人，這時車上有乘客54人，在火車站上車的有多少人？”

根據題目敘述的事情發展順序和生活實際得到的等量關系：原有人數-下車人數+上車人數=現有人數，列方程解答：

解：設在火車站上車的有人，根據題意得：

結語

如何利用等量關系提高小學生列方程解應用題的能力是小學教學中的重難點，以上這幾種方法便是本人在實際教學中總結的幾點。這幾點能夠幫助學生掌握利用等量關系列方程解應用題的方法，使學生的算式法解題思路轉變為方程法解題思路，對方程解應用題有更實質的理解。但是，這只是列方程解應用題的普遍思路模式，方法還有很多，最主要的是準確尋找等量關系，認真整理并分析，依據客觀實際情況，切勿只憑主觀意識就輕易對題目做出判斷。在實際教學中要結合學生學情歸納總結，力爭找到更有效的方法激發學生學習的興趣，建立學生做應用題的信心，實現提高學生的列方程解應用題的能力的更高目標。

參考文獻：

[1]黃育泉.列方程解應用題如何找等量關系[J]. 家長，1998（01）：36.

[2]莫瓊算.列方程解應用題中如何找等量關系[J]. 文淵（小學版），2019，000（006）：735.

[3]班亞峰.列方程解應用題如何尋找等量關系[J]. 人民教師論壇，2009（7）：38-38.

（作者單位：廣東省廉江市第五小學）