工程船舶開口角隅區域形式優化及疲勞分析

陳佰川

1.天津大學水利工程仿真與安全國家重點實驗室，天津 300072

2.天津大學天津市港口與海洋工程重點實驗室，天津 300072

在工業生產中，很多特殊用途結構物在制造過程中會設置局部開口以滿足某種實際需要，如海洋平臺的月池以及特種艦船的舷側和甲板開口等。據統計，一艘大型艦船在其服役期的20～25年內，承受的應力循環次數可高達107～108次之多[1]，而疲勞破壞是大型工程結構物的主要失效模式之一[2]。因此，結構物的制造工藝、外形和尺寸對疲勞破壞的影響是在設計中必須考慮的因素之一。

針對開口結構角隅處的形狀優化問題，韓春生[3]通過譜分析，研究了增設肘板和增加板厚對開口角隅處應力集中程度的影響；李霞麗[4]研究了在船舶甲板開口附近增設圍緣扁鋼的尺寸對角隅應力的影響；程玉芹[5]通過建立三艙段模型，對某艙口橢圓形角隅進行了形狀優化。Remes[6]針對開口部位研究了材料表面完整性對高強度鋼疲勞強度的影響。對于疲勞裂紋擴展問題，李國輝[7]通過預應力計算，預測了某鉆桿的疲勞壽命；胡艷華[8]對隔水管道進行了全尺寸試驗并觀察了疲勞斷口；唐昕[9]對儲氣井的套管和管箍進行了應力計算和疲勞分析；余建星[10]基于柔度法，對自主設計的開口角隅試樣進行了裂紋擴展參數數值計算。

本文選取某海洋石油工程作業船舶的舷側鋼板矩形開口為研究原型，首先利用有限元分析軟件對不同尺寸的圓形和橢圓形角隅進行了應力分析，進行了優化選擇，并探究了角隅應力的影響因素。隨后設計了多級應力水平模擬軸向加載并進行了平均應力修正，利用疲勞分析軟件FE-SAFE對若干角隅形式進行疲勞分析，擬合出優選角隅形式的理論雙對數S-N曲線，以供開口角隅結構設計時參考。

1 舷側鋼板開口應力集中

大型工程結構物在工業制造過程中，由于工藝、技術以及材料不均勻等原因，不可避免地會有夾渣、氣縫和初始裂紋等初始缺陷產生，特別是在焊縫和應力集中部位[1]。

海洋石油工程作業船舶常在舷側設置局部大開口而導致出現嚴重的應力集中現象，從而顯著地影響了舷側鋼板架的整體強度和疲勞壽命，這就要求船廠在鋼板制造前針對大開口尺寸和樣式謹慎地進行優化設計。圖1為海洋石油工程勘探船舶舷側開口鋼板架的應力集中情況數值計算云圖。

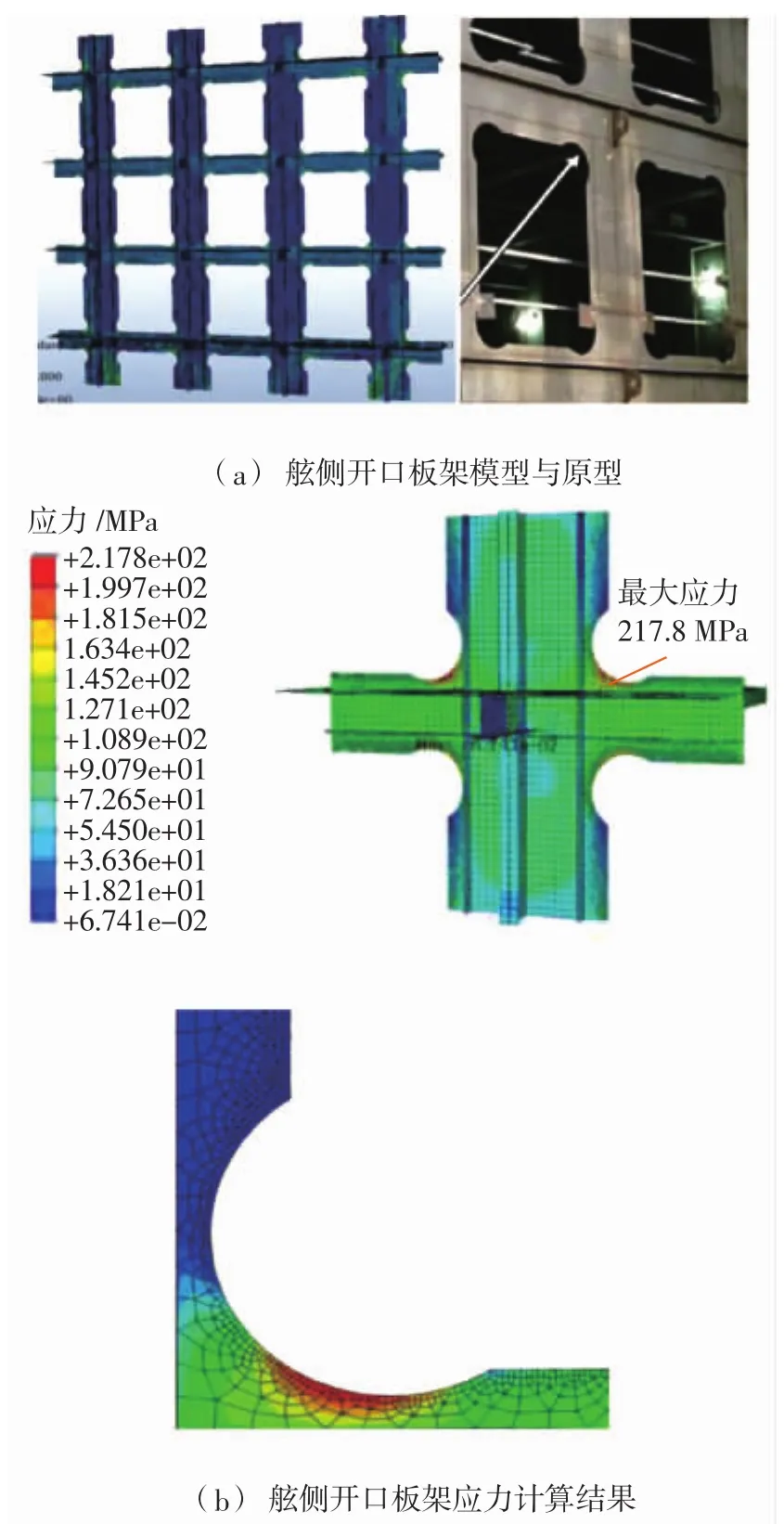
圖1 應力集中數值計算云圖

由圖1可見，開口結構的角隅區域由于幾何不連續而導致的應力集中情況較為嚴重，遠大于該結構其他區域的應力，所以開口結構的角隅處是疲勞強度設計和形狀優化的重點區域。

2 平板開口試樣數值計算

2.1 平板開口試樣模型建立

2.1.1 試樣基本參數

針對開口角隅形狀優化問題，本文設計的平板開口試樣以多功能作業船舷側鋼板的矩形舷窗開口為原型，利用有限元分析軟件對多組縮比尺模型進行試算后，確定試樣基底平板為長50 mm、寬60 mm的矩形，平板中央開口按照舷側開口原型尺寸縮小約80倍后取整，即開口矩形長26 mm、寬為22 mm。研究材料選擇船舶常用型鋼Q345鋼材，其材料參數如表1所示[11]，開口區域的原型和數值模型如圖2所示。在平板中央開口的上方和下方各預留一直徑為9.5 mm的圓孔，并將上圓孔的圓心設置為加載耦合點，為后續研究提供基礎數據和參考。

表1 Q345鋼材材料參數

圖2 平板開口試樣原型與數值模型

2.1.2 邊界條件和網格劃分

為模擬試樣軸向拉伸時的疲勞受力狀態，將上圓孔內表面的受力和位移耦合到圓心處，所有角隅形式的模型均在上圓孔加載耦合點處施加1 000 N豎直向上的力，在下圓孔內表面設置完全固定邊界條件。將模型按照角隅區域特點切割后，全局采用結構化六面體完全積分單元的網格劃分方式，全局網格單元幾何尺寸設置為0.8 mm，其中開口角隅處為重點研究區域，在四個角隅處需要將局部網格尺寸細化為0.4 mm。由于角隅處采用六面體結構化網格劃分時效果不佳，為了保證角隅處網格與模型主體網格平滑過渡，將四個角隅處網格屬性設置為六面體為主的掃略網格，如圖3所示。模型網格尺寸在加密前后計算結果僅相差1.2%，滿足計算精度要求，網格收斂性較好。

圖3 試樣網格劃分

2.2 開口角隅優化形式的確定

舷側鋼板的矩形開口在角隅處一般采用弧形過渡，本文選取橢圓形和圓形角隅進行對比研究。為了控制變量，在進行形狀比較時需要遵循等效性原則，即兩種開口角隅形式所占用的側板開口的面積相等，也即兩者在制造時的鋼板用量相同。開口角隅處需遵循的計算條件如圖4所示。為滿足等效性原則，只需使兩圖中的陰影面積相同即可，則其中一個角隅處需要滿足的關系式為：

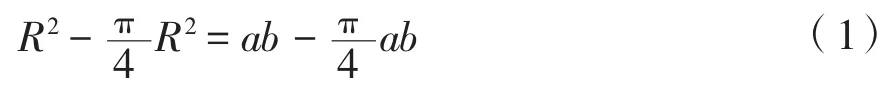
式中：R為圓形角隅半徑；a為隨圓長半軸，b為隨圓短半軸。

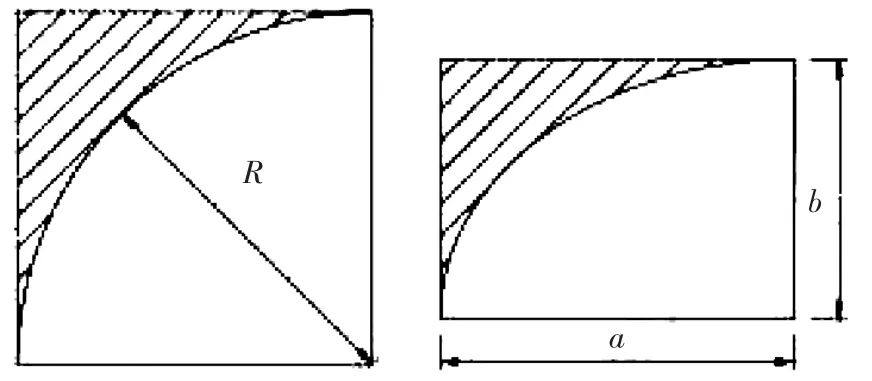
圖4 開口角隅處等效性原則示意

現設a為常數且為5 mm，則b和R為變量。為研究采用橢圓和圓形角隅時的應力對比，進一步規定圓角半徑R依次取為2.6～5.0 mm不等。將所取圓角半徑R的值分別代入式（1）后，相應的橢圓短半軸長度b以及橢圓度a/b的值也就相應確定下來。

2.3 角隅處應力數值計算結果

平板開口試樣的計算組次設置及應力數值計算結果見表2，其開口角隅處的應力曲線圖和有限元應力分析云圖示例分別如圖5（a） 和圖5（b）所示。為了避免模型縮比尺前后的尺寸效應對應力分析結果的影響，采用橢圓度a/b和圓角半徑R與開口矩形長邊l的比值R/l這兩個無量綱數，來描述角隅尺寸和形式變化過程對角隅處應力集中情況的影響。

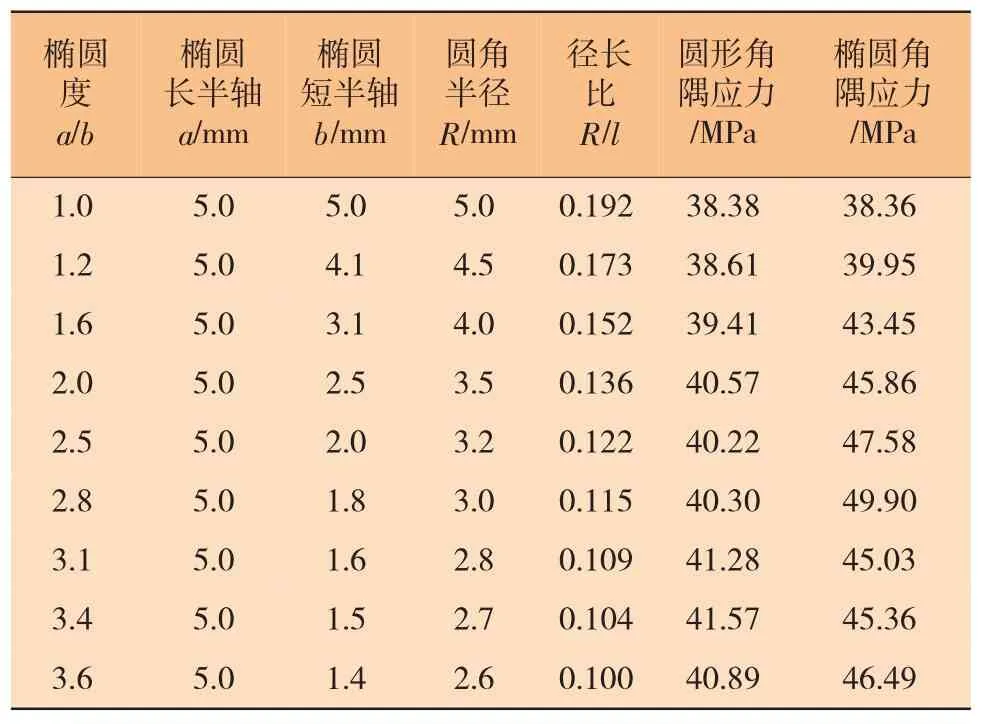
表2 角隅應力有限元計算結果

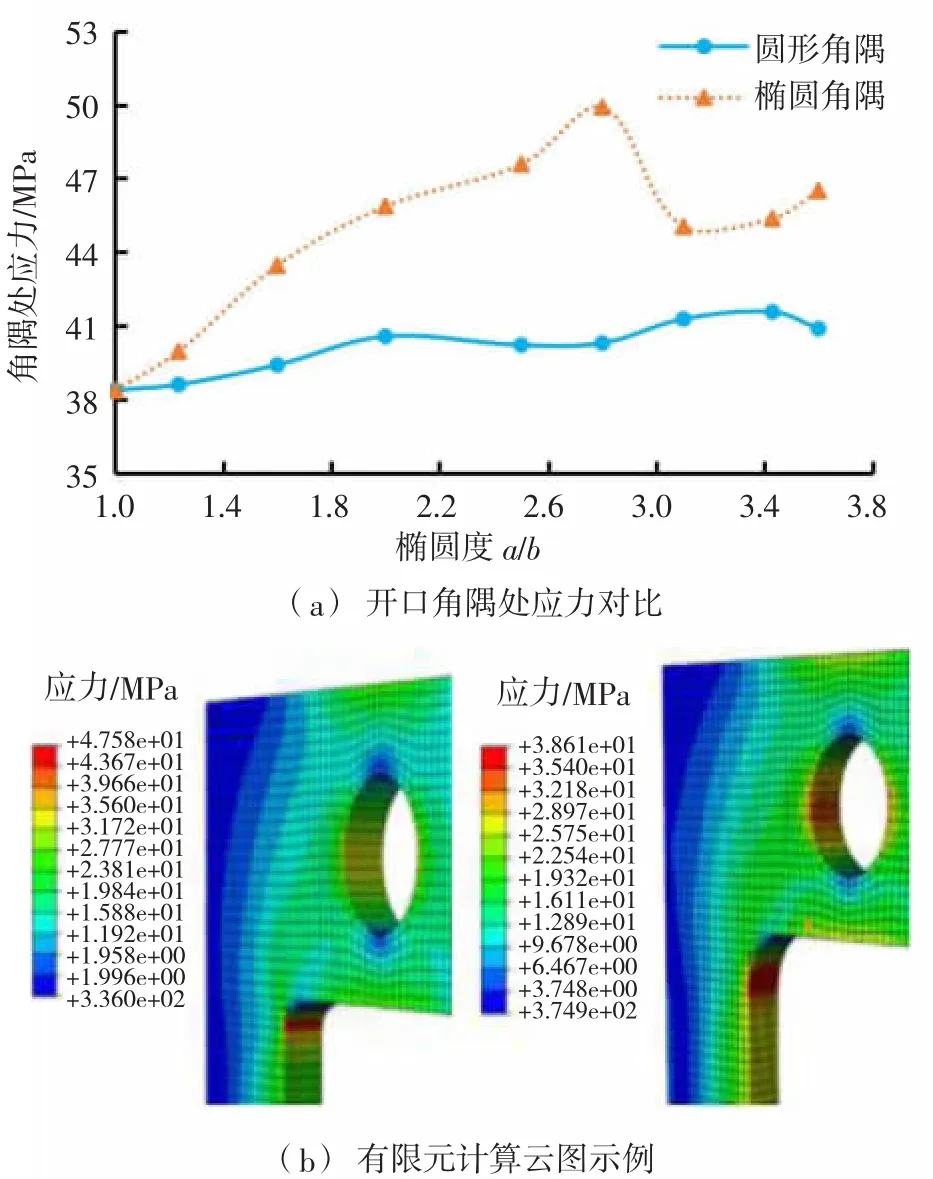
圖5 開口角隅處應力分析計算結果

有限元應力計算結果表明：在保證開口面積相同的情況下，采用圓形角隅時的最大應力總小于橢圓形角隅；隨著圓形角半徑R的增大，圓形角隅處的應力并非單調下降，而是有一定起伏波動，但總體仍呈下降趨勢。隨著橢圓形角隅的橢圓度a/b的不斷增大，角隅處最大應力整體呈上升趨勢，在a/b=3.1附近會有一個極小值點。如果某些開口結構需要采用橢圓形角隅，可選擇橢圓度a/b=3.1時的角隅形狀作為工程上的優化選擇。考慮工程實際和美觀需求，圓形角隅的半徑R也不能過大，否則可能影響正常使用，可選取徑長比R/l=0.192時的圓形角隅作為優選設計，此時應力集中情況較低，在承受相同的荷載時，可以獲得更長的疲勞壽命。

2.4 角隅應力影響因素探究

在角隅形式確定的情況下，鋼板本身的厚度、開口相對長度和開口長寬比等也會影響開口角隅處應力的大小。本節建立若干模型對以上影響因素進行了研究，其數值計算結果如圖6所示，圖中數據均以在開口角隅處取R=5 mm的圓弧為前提。

如圖6（a） 所示，隨著試樣厚度的逐漸增加，角隅處應力呈非線性降低，可用二次函數來表達厚度對開口角隅處應力的影響。由于矩形舷窗開口原型的長寬比為2 050 mm/1 732 mm=1.18，故保持模型開口長寬比l/w=1.18不變，改變開口矩形長度l與基底平板長度L的比值，即改變開口的相對大小，可知隨著相對開口長度l/L的逐漸增大，角隅處應力呈線性增長，如圖6（b）所示。保持開口相對長度l/L不變，改變開口本身的長寬比l/w，可見隨著l/w的逐漸增加，角隅處應力呈非線性下降，可用二次函數來表達開口長寬比對開口角隅處應力的影響，如圖6（c）所示；另外，在此圖中l/L=0.48和l/L=0.52兩曲線在橫坐標相同時，相應縱坐標之間的差值相等，且l/L越大，角隅處應力越大，進一步證明了開口相對長度對角隅處最大應力的影響是線性增加的。

3 角隅模型疲勞分析

3.1 平均應力修正

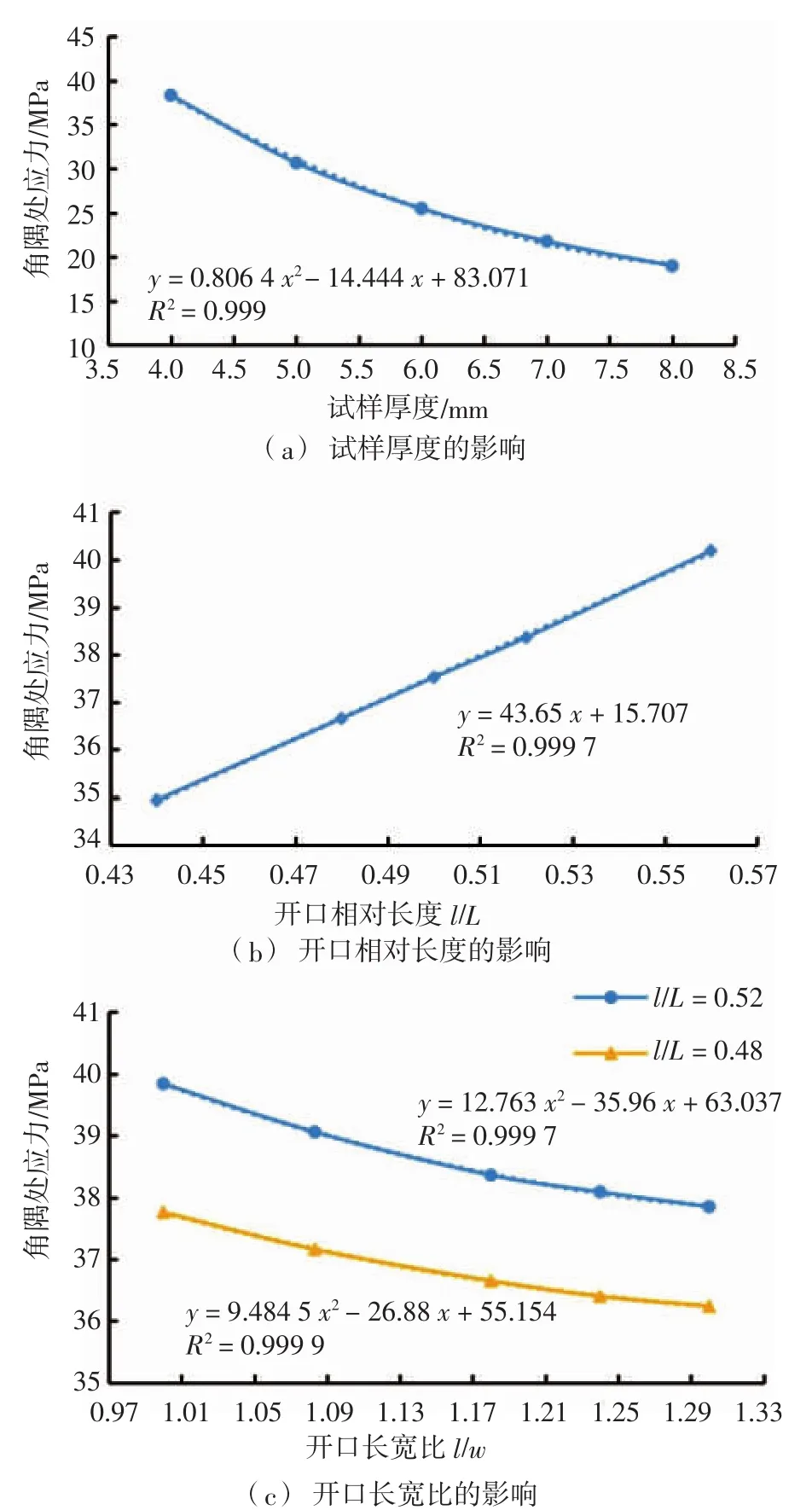
圖6 角隅應力影響因素計算結果

通常情況下，通過疲勞試驗和理論分析得到的S-N曲線，都是在受平均應力σm=0的對稱循環軸向拉伸荷載（應力比=-1）的應力條件下繪制的。在采用疲勞分析軟件FE-SAFE時，應將設計應力等效轉化為對稱荷載，然后再進行疲勞分析，常用的疲勞極限方程有Goodman直線方程、Soderberg直線方程和Gerber拋物線方程[12]，如圖7所示。

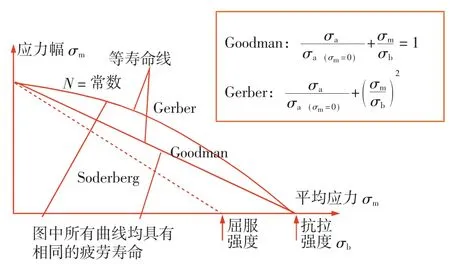
圖7 疲勞極限方程曲線

本文選擇經典的Goodman平均應力修正法，認為疲勞極限線是經過對稱循環應力的疲勞極限點和靜強度點的一條直線，其直線方程可表達為：

式中：σ-1為修正后的對稱荷載應力幅，σa為修正前設計荷載應力幅，σm為修正前設計荷載平均應力，σb為材料極限抗拉強度。

3.2 疲勞計算

選擇R分別為5 mm、4 mm和3.5 mm的圓形角隅模型，以及橢圓度a/b=2的橢圓角隅模型，進行疲勞計算。首先在有限元分析軟件中對加載點設置軸向拉力為1 N的荷載進行計算，采用與有限元分析時相同的單位制。選擇7級應力水平模擬試樣受多級軸向疲勞拉伸荷載，設計荷載的應力比取0.1。采用正弦波形的對稱荷載進行應力加載，錄入按照Goodman方法修正后的荷載幅，加載頻率為2 Hz。表面處理形式為鏡面拋光，采用默認疲勞算法進行疲勞分析。作為其中的優選形式，R=5 mm的圓形角隅模型加載設計和疲勞分析結果分別如表3和圖8所示。

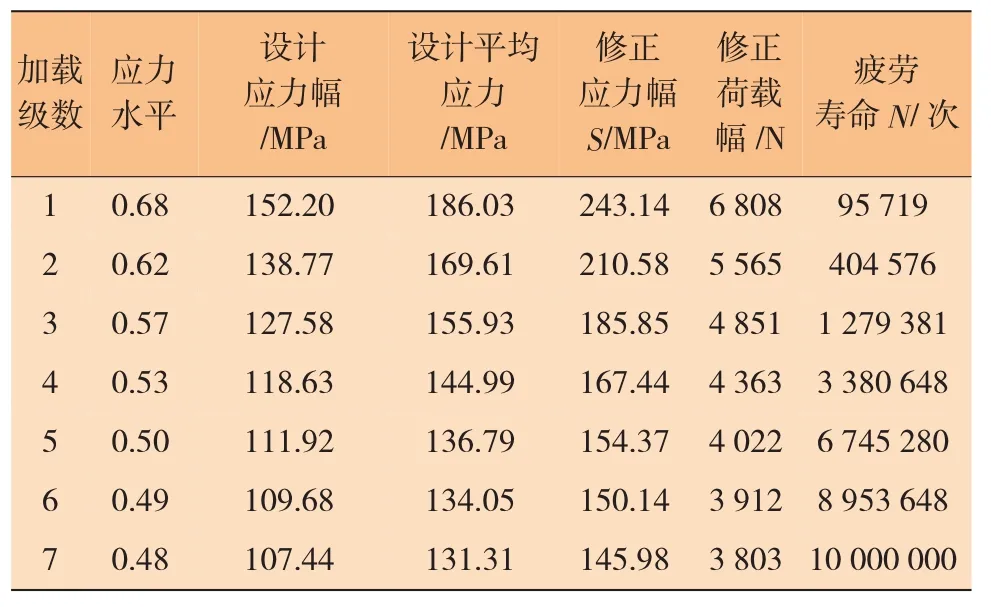
表3 FE-SAFE疲勞分析結果

3.3 S-N曲線

經過上述疲勞計算后，以Goodman修正應力幅S為y軸，疲勞循環次數N為x軸，可畫出各模型角隅區域的理論S-N曲線。為了線性化表達，通常將直角坐標系轉化為以10為底的雙對數坐標系，以得到lgS-lgN的線性表達形式，如圖9所示。

圖8 FE-SAFE疲勞分析結果（R=5 mm）

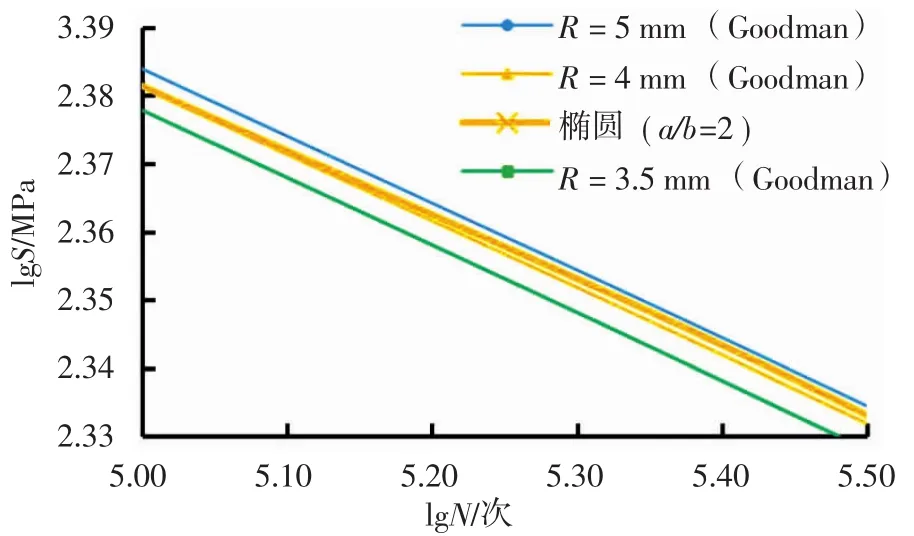
圖9 角隅區域lgS-lgN曲線

由圖9可以看出，在承受相同應力幅S的情況下，試樣疲勞壽命由高到低排序依次為R=5、4、3.5mm的圓形角隅和a/b=2的橢圓角隅，且R=3.5mm的圓形角隅和a/b=2的橢圓角隅是尺寸等效角隅，疲勞分析所得結果與表2中的角隅應力計算結果排序是吻合的，進一步證明了所得結論的正確性。使用最小二乘法擬合疲勞分析數據后，可以得到徑長比R/l=0.192（R=5mm）優選角隅形式的雙對數線性表達式為lgS=-0.1113×lgN+2.945，R2=0.9942。

4 結論

本文探究了圓形和橢圓形兩種角隅的形式，以及開口本身尺寸對應力集中的影響，利用FE-SAFE對若干角隅形式進行了疲勞分析，經計算得出以下主要結論：

（1）當開口角隅處選擇圓弧過渡且徑長比R/l=0.192時，平板開口試樣疲勞壽命最長，可以作為工程上的優化選擇。

（2）隨著試樣厚度的逐漸增加，角隅處應力呈非線性降低；隨著相對開口長度l/L的逐漸增大，開口角隅處最大應力呈線性增長；隨著開口長寬比l/w的逐漸增加，開口角隅處最大應力呈非線性降低。

（3）對于開口角隅處的優化問題，增加試樣板厚、優化開口角隅區域的形式以及改變開口本身的大小都是可行的。在船舶上的某些開口結構中，也可以通過在開口區域附近增設圍緣扁鋼并改變其厚度和尺寸的方式來減輕開口角隅區域應力集中的程度。

（4） 使用疲勞分析軟件FE-SAFE對若干開口角隅形式進行了疲勞分析并得到了優選角隅形式的lgS-lgN雙對數曲線，可為海洋工程船舶開口角隅區域的疲勞設計與后期維護提供參考。