基于混合模型的內容資源流行度預測算法

方元武, 何雪

(1.中國移動通信集團廣東有限公司, 廣東 廣州 510627; 2.廣州豐石科技有限公司, 廣東 廣州 510650)

0 引言

隨著互聯網內容井噴式上架和爆發式增長，對網絡服務商的服務器資源和網絡帶寬提出了更高的要求，內容的緩存命中率也極大影響著用戶的體驗[1]。如何在有限的條件下更合理地進行內容緩存是網絡服務面臨的主要問題，解決此問題的關鍵是需要一套科學決策方法對內容資源的流行度進行精準預測。精準的流行度預測不僅在用戶體驗上預知用戶行為，降低訪問時延，也能在網絡安全方面提前部署，減少因擁塞等問題導致的網絡溢出[2]。

預測領域經過多年的研究，已經在視頻[3]、社交[4]、新聞[5]、民生[6]、旅游[7]等多個行業應用，起到了很好的預測效果和指導作用，但是隨著社交互聯網的持續演進，現有研究對不同情況的預測卻稍顯不足。文獻[8]提出基于累計訪問次數方差的相關性構建時間序列模型，優于現有的流行度預測，但缺少考慮社交網絡行為帶來的話題影響，參數維度不足；文獻[9]提出基于logistic機器學習算法計算用戶行為信息，適用于消費數據稀疏的案例，對于長歷史數據缺乏參考意義；文獻[10]提出新型混合多回歸模型預測視頻流行度，該模型使用瀏覽時間和分享次數作為預測變量，考慮了用戶網絡行為，優于其他線性回歸模型，然而對時間序列樣本較多的數據，預測效果欠佳。

本文結合已有研究，以社交網絡數據為基礎，提出一種不限歷史數據長短的內容資源的流行度預測算法。分別針對歷史數據稀疏的資源和長歷史特征數據的資源采用線性回歸算法和ARIMA時間序列算法。對比傳統的流行度預測，這種混合的流行度預測算法，既適應稀疏數據的局部性特征也能適應長歷史數據的季節性變化特征，表現出更高的預測精度。

1 流行度預測算法

1.1 算法流程介紹

流行度是度量內容資源熱度的重要指標之一。對流行度的預測，機器學習是運用的較多的一種方法，然而機器學習通常需要基于大量樣本進行模型訓練，以提高預測精度[11]。對于上新或者數據周期短的內容資源，機器學習算法預測效果明顯失真[12]。為了適應不同情況的內容資源預測，實驗采用基于線性的多元回歸和基于時間序列的ARIMA模型結合的混合預測模型。多元回歸預測適用于數據稀疏的內容資源，ARIMA算法適用于樣本數據較大并且具備季節性周期的數據。這種混合模型通過互補的方式，提高了預測的包容性，能夠在變化的環境中保證一定的預測精度，如圖1所示。

圖1 內容資源的流行度預測模型算法流程

1.2 基于多元回歸的流行度預測算法

數據稀疏內容資源呈現出歷史數據的局部性、相鄰時間記錄的強相關性的特點，正好與多元回歸算法切合[13]。基于內容資源流行度的多元線性回歸預測算法，如式(1)。

(1)

式(1)利用最近t-1(t<=7)天的流行度預測第t天的流行度，Y(t)即為預測結果。Ni為內容資源在第i天流行指數(見公式(1))，βi為第i天的權重，εt(t=1,2,…,n)是隨機項誤差，α是常數，n為天數。

受社交網絡的影響，內容資源的流行程度不一，對于突發性的內容可能經過前期潛伏之后，后期呈指數級別上升，前后產生巨大的差距，容易因預測計算溢出導致結果失真。應對這種情況，可以在線性回歸的基礎上進行對數處理，然后基于對數結果預測內容資源流行度。這樣的做法在保持原數據單調性的同時，也能弱化數據變化的敏感度。通過多元指數線性變換和對數變換建立多元對數回歸模型。

多元指數線性回歸模型，如式(2)。

(2)

對數變換公式，如式(3)。

(3)

1.3 基于ARIMA的流行度預測算法

ARIMA[14]模型是一種只考慮數據內在聯系的時間序列算法，更適用于長歷史特征的數據分析。ARIMA包含3個部分，AR代表的自回歸模型(Autoregression)；I代表的差分運算(Intergrated)；MA代表的移動平均模型(Moving Average)。自回歸項p，差分階數d，移動平均項數q分別是自回歸模型、差分運算和移動平均模型的參數[15]，取值皆為非負整數，用ARIMA(p,d,q)表示。

經過差分處理使序列趨于平穩化后的ARIMA(p,d,q)模型表示，如式(4)。

(4)

式中，{Ni-p,…,Ni-2,Ni-1,Ni}表示該時間序列數據；B表示延遲算子；{εi-q,…,εi-2,εi-1,εi}表示隨機干擾序列；{φ1,φ2,…,φp}、{θ1,θ2,…,θq}分別表示自回歸系數和移動平均系數；d=(1-B)d表示d階差分；S表示季節周期。

2 實驗

2.1 數據收集

本文通過編寫爬蟲程序，爬取了Alexa網站、中國站長站、微博等網站，收集包括訪問量、瀏覽量、搜索指數、話題熱度等數據。為了使數據更加易于處理，剔除了訪問量、瀏覽量小于100的資源，最后剩余8 304個樣本資源。

2.2 數據準備

社交互聯網的新時代，單純以訪問量、流量評估流行度已不足以滿足對內容資源的評價，話題次數、搜索次數也對資源流行程度產生重要影響。因此，結合網絡行為特征，選取訪問量、瀏覽量(PV)、搜索指數、話題熱度為參數對資源的流行度進行評價，如式(5)。

Ni=w1(v,i)+w2(p,i)+w3(s,i)+w4(t,i)

(5)

式中，Ni是第i個資源的流行指數，w1,w2,w3,w4分別是訪問量、PV、搜索指數及話題熱度對流行指數的影響系數。

經過流行指數評價標記，得到所有樣本資源每天的流行度指數，流行度d值越大代表資源的網絡流程程度越高。樣本數據，如表1所示。

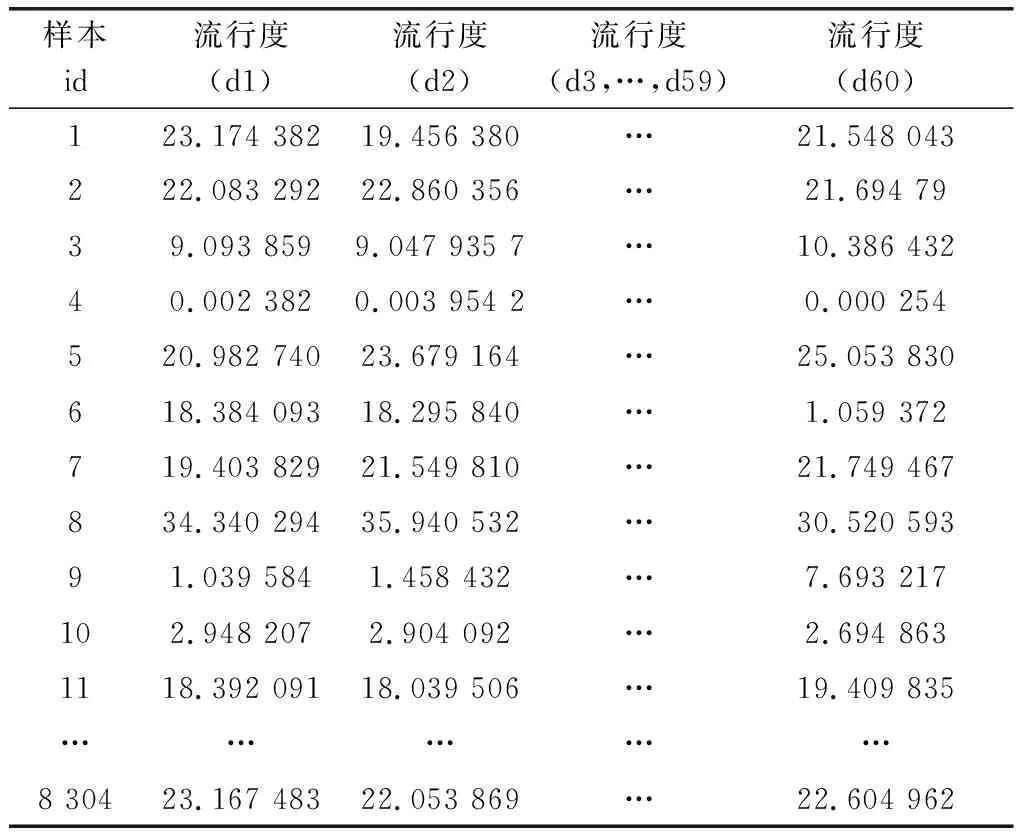
表1 內容資源流行度樣本數據

2.3 數據建模

根據圖1的算法流程，按照數據是否低于7天將上述數據拆分為的稀疏資源和長歷史特征資源，分別對其進行線性對數回歸模型構建和ARIMA模型構建。

1.多元對數回歸模型構建

數據范圍在一周內的數據樣本共23個，將23個樣本數據按照線性模型方程進行線性指數求和，然后對指數和進行對數變化，得到方程的解，如圖2所示。

圖2 多元對數回歸計算結果

如圖2，(1) 判定系數R2=0.958 513，接近1，說明稀疏數據資源第t天與第t-1,t-2,…，1天的流行度存在強相關性，擬合程度較高[16]。

(2) 統計量F=341.502 2，若取顯著性水平α=0.05，由F分布表查詢臨界值F0.05(6,15)=2.79<341.502 2，表示y(t)與N1,N2,…,Nt之間不存在顯著差異，即存在相關性。

2.ARIMA模型構建

步驟一：序列平穩化，差分定階。按照算法流程將一周以上的樣本數據進行時間序列呈現。逐步對時間序列進行階數的差分處理使序列平穩；經過二階差分，單位根(ADF)檢驗序列得到統計值為-7.231，落在1%的置信區間，概率小于0.05，因此確定差分階數d=2。

步驟二：參數估計。利用Eviews軟件計算得到平穩序列后的自相關圖和偏相關圖，如圖3所示。

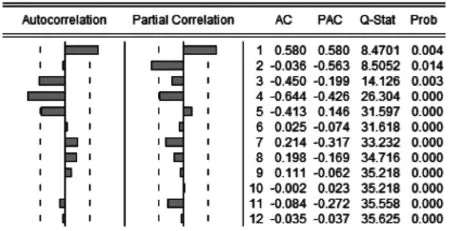
圖3 序列差分后的ACF圖和PACF圖

自相關系數在滯后4階的時候落在2倍標準差的邊緣，PACF呈二階拖尾，因此q可以考慮取1或4，p可以取1或2，對模型進行檢驗，如表2所示。

表2 模型檢驗結果

參數(2,1)的AIC和SC檢驗參數最理想，確定模型為ARIMA(2,2,1)。

步驟三：模型適應性檢驗。檢查模型的殘差是否相關，平均分布是否為0。因此，獲取計算結果的值進行模型診斷，如圖4所示。

(a)

(b)

圖4(a)時間序列中，殘差沒有明顯的周期性變化；圖4(b)對殘差進行差分計算，發現時間序列殘差與其本身的滯后版本沒有明顯的自相關性。綜上，判斷殘差為白噪聲。實驗構建的ARIMA(2,2,1)模型對長周期序列的內容資源流行度預測是合適的。

2.4 模型預測

將上述已確定參數的多元對數回歸模型和ARIMA模型組合為混合模型，并輸入歷史數據，利用混合模型預測未來流行度指數。模型預測情況，如圖5所示。

圖5 混合模型內容流行度預測情況

由圖可知預測值與實際值高度重合。

2.5 MAE模型性能評估

采用MAE(平均絕對誤差)方法評估混合模型實際預測誤差，如式(6)。

(6)

實驗分別對文章提出的混合模型(mixture)與其他文獻中提到的基于線性回歸模型預測方法(linear-model)、基于對數回歸模型預測方法(log-model)以及基于ARIMA模型的預測方法進行對比，如圖6所示。

圖6 預測絕對誤差率對比結果

由圖可知，實驗中的混合預測方法的預測絕對誤差率低于0.38%，誤差率最小。

3 總結

為實現對不同歷史數據周期內容資源的流行度預測，本文結合多種統計學方法，在對基礎數據預處理后，分別對短周期資源和長周期資源進行多元對數回歸算法流行度預測和ARIMA時間序列算法流行度預測。經過誤差分析和對比后，得到的混合模型絕對誤差率在0.38%以下，優于其他模型方案。該模型可以基于歷史數據，為互聯網服務商在資源緩存方面提前規劃提供指導，提前布局。在結合實際應用的過程中，可以擴大樣本數據范圍，利用現代科技的大數據處理能力和人工智能技術，挖掘更多特征信息，提升數據的科學決策能力。