機器人機械參數辨識與誤差補償方法

趙瑜, 宋雪, 馬松杰

(延安職業技術學院 機電工程系， 陜西 延安 716000)

0 引言

機器人已經廣泛應用于搬運、焊接、噴涂、裝配、加工等領域的方方面面，深刻地改變了工業體系的構成，成為現代社會分工中不可缺失的重要一環。隨著工業自動化、智能化水平的不斷提高，機器人的功能也在不斷擴大，多機器人協調控制、機器人離線編程等新技術成為未來工業機器人的主要發展方向；而另一方面，工業機器人自身也朝著大負載、輕質的方向的發展，在此背景下，通過機器人本體的優化設計及應用更加先進的模型控制方法成為機器人制造商提升產品性能的必由之路，也正是國內外學者的研究熱點問題[1-3]。

機器人設計具有多設計輸入及多設計輸出的特點，且各設計參數之間往往存在著耦合關系，這種特點一方面給模型參數的精確獲取帶來很大難度，另一方面也制約了優化設計的應用范圍。這也正是機器人在設計中仍主要依賴經驗，在控制中仍主要采用傳統的PD/PID的控制方法的原因。國內外知名的工業機器人制造商聯合科研院所，在運動學標定及運動學優化、動力學標定及動力學優化等方面開展了大量研究，在一定程度上提升了機器人的設計水平[4-6]。但是已有的研究集中在完成機器人本體設計后的靜態設計參數，如運動學參數中的DH參數，動力學參數中的質量和慣量參數，而忽略了機器人關節柔性、摩擦等受機器人位姿、速度、加速度等因素影響而呈非線性特點的動態參數的影響，因此模型參數的辨識不全面、不精確，從而導致機器人控制的誤差提高不明顯，動態性能差；與此相關地，針對機器人運動學與動力學的優化模型由于沒有考慮動態參數的影響，優化設計的結果更加側重于機器人的局部性能指標的實現，對機器人結構設計的指導意義不強[7-10]。

1 參數辨識及優化方法研究中的主要問題

機器人參數辨識及優化方法的研究中主要問題如下。

(1) 運動學參數中的柔性參數辨識問題。當前的機器人參數辨識研究基本解決了參數辨識模型的奇異解問題以及基于開環測量和閉環測量的試驗參數獲取問題。但仍然存在不足的是，對關節和連桿柔性變形等動態因素所造成的參數辨識精度影響的研究較少，現有的柔性參數辨識與DH參數辨識相對獨立，柔性參數辨識的結果僅應用于剛度分析及控制中。而隨著機器人向輕質、重載的方向發展，工業機器人柔性參數對機器人整體精度的影響越來越深。由于機器人關節的復雜傳動關系，機器人關節剛度模型并非簡單的線性關系，CCT 的模型的缺點是未能反映出剛度模型非線性的特點。因此，有必要在現有 CCT 模型的基礎上，建立機器人關節的精確剛度模型，并對模型中的剛度參數進行精確辨識[11-14]。

(2) 機器人動力學參數中關節摩擦參數的辨識問題。當前機器人動力學參數的辨識大都將關節摩擦處理為Coulomb 模型加 viscous模型的形式，并對模型線性化處理后與慣性參數同時辨識，然而該摩擦模型與第 3.3.2 節所述第四種模型相比，不能真實反映機器人關節摩擦在低速區的實際狀態，而第四種模型雖然能夠精確反映機器人關節的摩擦特點，但由于不像 Coulomb摩擦加 viscous摩擦的模型易于線性化處理，在機器人動力學參數辨識中的應用受到限制。

(3) 機器人綜合性能優化方法問題。當前有關機器人性能的優化方法的研究大都針對于機器人性能的一個或局部幾個指標， 從而難以實現機器人綜合性能的優化，造成機器人僅在某幾個性能指標上表現突出。然而，出于柔性化的需要，用戶對機器人的要求是多方面的，機器人制造商在設計階段應保證機器人綜合性能的最優化。由于機器人具有多設計輸入及多設計輸出的特點，實現設計階段的綜合性能優化十分必要，但這方面的研究尚不充分[15-18]。

2 法向姿態誤差校準

機器人鉆鉚加工不僅需要機器人具有較高的絕對定位精度，還對機器人的法向定位精度提出了很高的要求。視覺測量雖然解決了機器人與實際蒙皮坐標系之間的校準，但由于飛機蒙皮尺寸較大，在蒙皮的局部區域仍存在由于自身重力作用而產生的實際法向量偏離理想法向量的現象，這種誤差的存在必然會影響打孔的法向姿態精度。法向姿態誤差校準就是為了消除這一偏差[19-20]。

2.1 測量原理

校準的原理是通過四個激光測距傳感器測量得到機器人末端執行器距離飛機蒙皮某目標區域的相對位置，再借助機器人自身坐標系以及激光測距傳感器坐標系之間的相對位姿關系獲取目標區域的實測法向量。將實測法向量與理想法向量進行比較便可獲得蒙皮目標區域的實際法向量偏差，最后由機器人對這一偏差進行糾正。

2.2 設備組成

激光測距傳感器及其標定裝置,如圖1所示。

圖1 機器人法向姿態誤差校準示意圖

2.3 校準步驟

(1) 激光測距傳感器相對位置標定

由于涉及中激光源與機器人末端坐標系的相對位姿關系為理論值，并未考慮由于安裝造成的位姿誤差，而這一誤差對最終的測量結果影響較大。因此應設計專用的校準工具，校準工具與機器人的末端執行器已知基準相互配合，用來完成對激光測距傳感器的相對位置標定。

(2) 目標區域測量

將機器人移動至目標區域的上部規定距離，開啟四臺激光測距傳感器進行測量。激光測距儀將測量得到的線性距離傳回機器人控制器，控制器便可根據這一信息結合已標定完成的機器人末端執行器與激光測距傳感器之間的相對位姿關系計算四個測量點的位置信息，如圖1所示。

(3) 實測法向量計算與偏差補償

最后對比實測n與理論n之間的偏差，并對這一偏差進行補償。

3 誤差補償測量原理

3.1 設備組成

機器人定位精度網格補償示意圖,如圖2所示。

圖2 機器人定位精度網格補償示意圖

3.2 基于柔性變形模型的機器人絕地定位誤差補償

機器人產生絕地定位誤差Δp主要由DH參數、關節及連桿變形等誤差組成。可表示為機器人實到位姿pr與指令位姿pt之間的差值，結合機器人的構成及控制系統的運動學模型及已有的研究成果，可定位誤差Δp的來源組成，如式(1)。

Δp=Δpg(q,φ)+Δpe(q)+Δpf(q,W)+Δpc(q)+

Δpb(q,sign(W))+Δpo(temp,noise)

(1)

式中各參數意義如下。

q：機器人各個關節的角位移；

φ：幾何參數，主要由DH參數組成；

W：關節和連桿受力；

Δpg：幾何誤差，即由幾何參數造成的位姿誤差；

Δpe：關節柔性誤差，由關節柔性變形產生的位姿誤差；

Δpf：連桿柔性誤差，由連桿柔性變形產生的位姿誤差；

Δpc：由關節驅動不同軸造成的位姿誤差；

Δpb：由關節的驅動系統齒隙造成的位姿誤差；

Δpo：其他非幾何誤差，包括驅動誤差、溫度誤差等。

已有研究表明幾何誤差和柔性變形誤差是機器人絕對定位誤差的主要來源，前者主要由機器人DH參數的誤差造成，DH參數對幾乎任何構型的機器人來說都是常數，后者則與關節回差、關節傳動不同軸參數、溫度影響參數等同屬于非幾何參數，主要來自于機器人關節和連桿的柔性變形，而柔性變形是與機器人的位形和柔性系數相關的變量。由于關節不同軸誤差、關節回差、關節驅動誤差、溫度變化誤差等對機器人整機定位誤差的影響很小，而柔性變形在整個機器人未建模誤差中所占比重有的高達50%-70%，因此在針對本項目重載機器人的定位誤差補償中選擇DH參數和柔性參數作為辨識和補償的對象。

首先根據所建立的機器人運動學模型和柔性變形模型，根據以下步驟進行各個參數的辨識。

(1) 零位參數辨識：在未進行機器人零位標定前，零位參數誤差在所有運動學誤差中占主要成分，其數量級大于其他運動學參數。因此進行零位參數辨識是進行更為精確的機器人運動學參數辨識的基礎；

(2) 零位參數辨識完成后得到機器人零位的關節值q0，在此基礎上機器人處于零位置時的關節和連桿載荷W0；

(3) 優選出分布在機器人工作空間中的一組測量位姿，分別進行N組機器人位姿信息 的測量，同時獲取每組位姿對應的關節值qi(i=1,…,N)；

(4) 根據第i組qi值，進行以下誤差值的計算：

◇計算辨識雅克比矩陣Ji；

◇計算指令位姿pt；

◇計算關節和連桿的受力W0和Wi，從而得到W=Wi-W0；

◇計算關節柔度變形Δpe和連桿柔度變形Δpf；

◇ 計算運動學參數造成的位姿誤差Δpgi=pr-pt-Δpf-Δpe；

(5) 將N組Ji和Δpgi分別整合為JN和ΔpgN；

(6) 辨識運動學參數Δφ。

3.3 基于柔性變形誤差補償實施方案

機器人柔性變形誤差補償是在完成運動學參數辨識及補償及柔性參數辨識的基礎上，對機器人本體的關節和連桿的柔性變形誤差進行的在線補償，如圖3所示。

圖3 機器人柔性變形誤差補償示意圖

包括以下兩個方面。

(1) 機器人關節柔性變形誤差的補償。在輸入機器人期望位姿Td后，機器人的目標關節值qd可通過對位姿矩陣的逆解求得，將其作為關節誤差模型的輸入計算出在期望位姿下關節的變形值 Δqe，并將其負值作為關節補償量加入到目標關節值qd中。

(2) 機器人連桿柔性變形誤差的補償。在輸入機器人期望位姿Td并通過對位姿矩陣的逆解求得qd后，將其作為連桿誤差模型的輸入計算出在期望位姿下的姿態變化值 ΔT，根據雅克比矩陣求出對應的關節值補償量Δqf，并將其負值作為關節補償量加入到目標關節值qd中,如圖4所示。

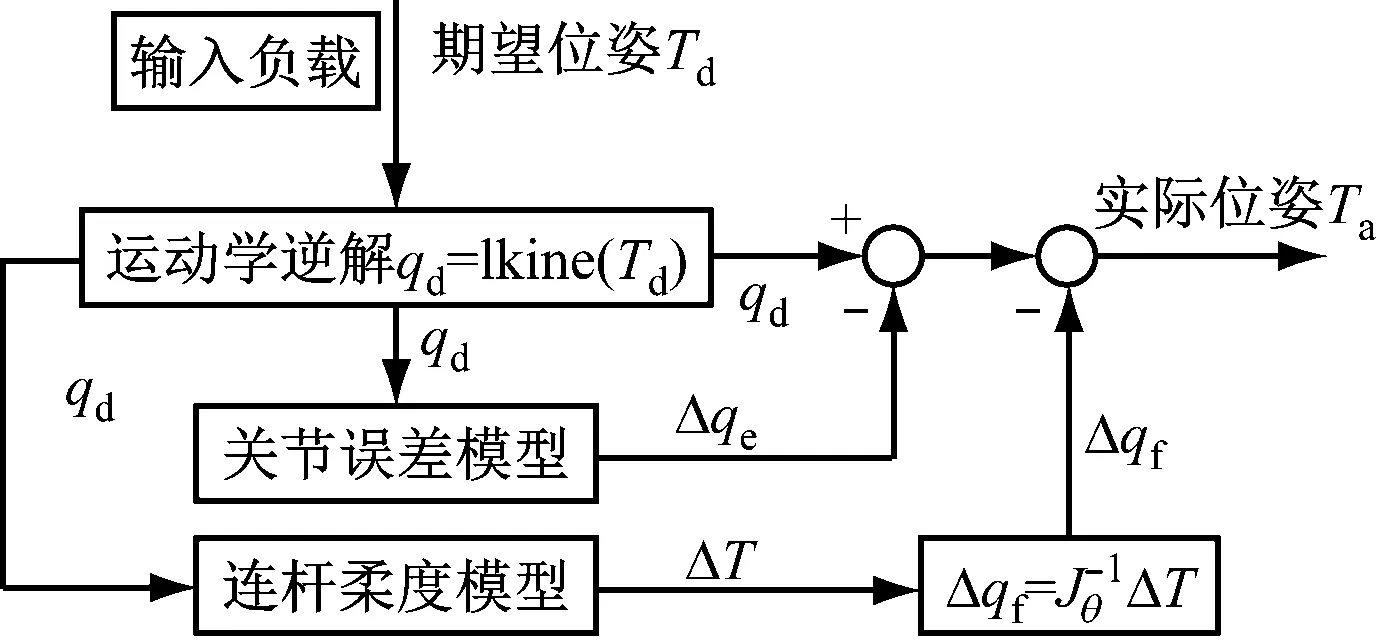
圖4 機器人柔性誤差補償示意圖

3.4 基于網格法補償法的機器人絕對定位誤差補償

網格補償法屬于非運動學模型的補償，如何有效劃分整個工作空間并根據離散網格點的誤差值估計整個連續空間的誤差是該類補償方法的研究重點,具體方法如下。

首先對蒙皮的三維CAD模型進空間網格劃分，將得到的網格節點作為目標點，根據機器人及蒙皮的理論相對位置計算出這些目標點的在機器人坐標系下的理論坐標值。根據機器人補償精度的要求，可以把機器人工作空間劃分為網格,如圖5所示。

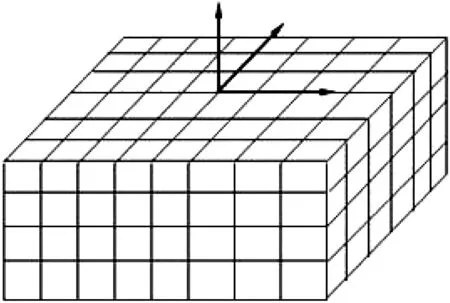
圖5 機器人工作空間網格的劃分圖

然后使機器人末端工具點(靶球中心)到達各個目標點處，利用激光跟蹤儀量各到達點的實際位置，得到相對應的理論值與實際值的誤差值，應用反距離加權算法對整個工作空間進行誤差補償,各方向補償公式,如式(2)—式(4)。

X方向的誤差補償,如式(2)。

(2)

Y方向的誤差補償,如式(3)。

(3)

Z方向的誤差補償,如式(4)。

(4)

式中,Li、Lj、Lk分別為X方向、Y方向和Z方向的網格點，Lxi、Lyj、Lzk分別為X方向、Y方向和Z方向的位置補償值。

5 總結

機器人模型是性能分析和控制的基礎，比較重要的機器人模型有運動學模型和動力學模型，相應的機器人模型參數有運動學參數、動力學參數。在實際應用中，機器人的運動學參數(主要是DH參數)常在控制器中被預先設定，直接參與機器人的運動學控制。因此，運動學參數的精度直接決定了機器人的精度性能。當前的研究已經解決了DH參數辨識的建模、辨識、測量等關鍵理論和技術問題，但有關柔性變形、齒隙等動態參數對機器人定位精度的影響還缺乏足夠的理論研究。

機器人設計過程中面臨過多的設計輸入參數與輸出參數，其設計過程一直被科研人員視為一個典型的參數優化過程。作為設計階段實現機器人性能優化提升的有效手段，有關機器人全域性能指標的研究還不完善，不能滿足設計階段機器人的優化設計需求。本文提出首先基于柔性變形模型補償的機器人絕對定位誤差補償方案。綜合機器人幾何學性能、運動學性能和動力學性能的研究成果，提出機器人綜合性能的合理評價指標，并在機器人參數辨識的基礎上，對機器人進行綜合性能評價和全局優化方法的研究。