LFM-BPSK復合調制參數快速估計及碼元恢復
李 娟,戴曜澤
(1. 南京科瑞達電子裝備有限責任公司,南京211100; 2.中國航天科工集團8511研究所,南京210007)
0 引 言
隨著電子技術的發展,LFM-BPSK復合調制波形具有良好的抗干擾、低截獲、多普勒不敏感等優點,在脈沖壓縮雷達中得到越來越廣泛的應用。因此,如何在復雜的電磁環境中有效、快速地偵察、分析及估計出此類復雜雷達調制信號以實現對新體制雷達進行準確迅速截獲具有很強的作戰應用意義。
目前,國內外已有不少文獻提出了各種參數估計的方法。文獻[1-2]提出小波變換、相位擬合、相位譜商特性等參數估計算法,但計算量大。最大似然法[3]、基于循環譜最小均方誤差法[4]、基于二階統計量最大似然法[5]等計算量小,但這些方法多是基于合作接收機或已知部分先驗知識的前提。在電子偵察中,由于沒有任何先驗知識,這些方法的性能都會下降甚至失效。Gardner等提出了基于循環譜的幅度特征的相位編碼信號盲估計參數估計方法[6],但由于計算量大、數據儲存空間大等缺點,不適宜電子偵察的實時處理。文獻[7-9]提出了基于Wigner時頻分布的偵察信號參數估計方法,但需要在時頻平面進行二維搜索,計算量也較大。
本文基于信號的平方、短時積分及短時傅里葉變換運算對LFM的調頻斜率、初始頻率及BPSK的碼元速率進行了快速參數估計,其計算量和存儲空間需求較小,可在硬件中實時實現。
1 信號模型
LFM-BPSK復合信號的相位為
(1)
式中,k為調頻斜率,f0為初始頻率,Tb為碼元寬度,N為碼元個數,∏為持續時間為Tb的矩形窗,當且僅當0≤t 由式(1)可得LFM-BPSK復合信號的表達式如下: (2) 式中,φ0為信號的初始相位,Tb為碼元寬度,NTP為脈沖的持續時間。 LFM-BPSK信號的時頻曲線兼具了LFM與BPSK的特點,其時頻曲線如圖1所示。LFM-BPSK信號平方后的時頻曲線僅剩LFM的特點,其時頻曲線如圖2所示。 圖1 LFM-BPSK信號時頻圖 設偵察接收機接收的信號1如下: 圖2 LFM-BPSK信號平方時頻圖 (3) 式中,w(t)為均值為0、方差為σ2的高斯白噪聲。此仿真假設已提取出脈內信號,即信號的脈寬T=NTP已知,在此基礎上估計LFM-BPSK信號的起始頻率f0、調制斜率k、初始相位φ0、碼元寬度TP并對碼元進行恢復。 由圖1可知,若實現LFM信號的起始頻率f0和調制斜率k的估計,必須先消除BPSK的相位突變,然后利用快速解線性調頻的算法解算出LFM信號的起始頻率f0和調制斜率k。由圖2可知,LFM-BPSK信號的平方可消除BPSK的相位突變,LFM的起始頻率f0和調制斜率k經平方變為2f0和2k。其具體的解算過程如下: (1) 將式(3)平方得 x2(t)=[s(t)+w(t)]2 =s2(t)+2s(t)w(t)+w2(t) =ej(4πf0t+2πkt2+2φ0)+w2(t)+2w(t)× =slfm2+w′(t) (4) 式中 slfm2(t)=ej(4πf0t+2πkt2+2φ0) (5) (6) 因此,x2(t)可看成一個被噪聲w′(t)污染的起始頻率為2f0、調制斜率為2k的線性調頻信號slfm2(t),要估計線性調頻參數可用快速線性調頻算法進行計算。 (2) 估計線性調頻slfm2(t)斜率 =ej(4πf0t+2πkt2+2φ0)×e-j(4πf0(t-τ)+2πk(t-τ)2+2φ0) =ej(4πktτ+4πf0τ-2πkτ2) (7) (8) (3) 估計線性調頻信號slfm2(t)起始頻率 (9) (10) 由式(3)可知,平方運算消除了復合調制的相位突變,從而將復合信號參數估計問題轉換為線性調頻信號參數估計問題,避免了時頻分析的二維搜索。但是,由式(4)可知,由于平方運算造成了信噪比的降低,因此算法無法適用信噪比過低的場合。信噪比低于-2 dB時,由于噪聲的影響會造成信號檢測錯誤,從而使參數估計失敗。因此,在應用此算法前應用時域、頻域濾波等方法提高信噪比。另外,信號平方后還可能導致f2頻率模糊問題,因此在計算f2時要利用原復合信號頻率所在的位置對f2進行解模糊。 由2.1節可重構線性調頻信號為 (11) 根據式(4),原信號平方后與重構信號的平方共軛相乘為 =[ej(4πf0t+2πkt2+2φ0)+w2(t)+2w(t)× =ej(4πΔf0t+2πΔkt2+2φ0)+w2(t)+2w(t)× (12) (13) 因為w(t)為均值為0、方差為σ2的高斯白噪聲,式(13)可簡化為 (14) 通過2.2節可重構出帶初相的線性調頻信號為 (15) 原信號與重構信號的共軛相乘得 (16) 圖4 相位編碼碼元速率 由圖3、4及誤差率可看出,信噪比為5 dB時可精確估計出復合信號的參數。可見,短時積分能夠快速實現碼速率的快速精確估計。但是,在選擇積分長度T0時,要滿足T0 (17) (1) 對BPSK_base信號取實部,其圖如圖5(a)所示。圖中,“……”表示原始碼元,“┅┅”表示含有噪聲和誤差的碼元。 (2) 對含有噪聲和誤差的碼元以0為門限進行1,-1判斷,當碼元大于或等于0時碼元判斷為1,否則碼元為-1。經過門限判斷后的圖如圖5(b)。圖中,“……”表示原始碼元,“┅┅”表示經過門限判斷過后的碼元。 (3) 由圖5(b)可知,由于噪聲和估算精度的影響,會造成碼元存在毛刺,利用積分算法對碼元進行去毛刺。去掉毛刺后的碼元如圖5(c)。圖中,“……”表示原始碼元,“┅┅”表示去掉毛刺后的碼元,可看出去掉毛刺后的碼元與原碼元完全重合,在此基礎上對碼元進行恢復。 (4) 在利用計數恢復碼元時,由于碼元速率誤差會使碼元恢復過程中的誤差個數隨著碼元個數的增加而增大。比如,第1個碼元有1個采樣點的誤差,則第2碼元則有2個采樣點的誤差,以此類推。當第100個碼元時則會出現100個采樣點的誤差,從而可能無法正確恢復出碼元。因此,在碼元恢復過程中,要利用碼元的突變對計數器進行清零,去除積累誤差,然后找碼元的中值點,利用中值點的數值對碼元進行賦值。 圖5 碼元恢復過程 本文提出的LFM-BPSK復合信號參數快速估計及碼元恢復算法以FFT運算為核心,輔以少量的乘法運算和正余弦運算,無矩陣相關運算。信號平方、延時共軛相乘及翻轉共軛相乘主要是復數乘法可調用mul核實現,在計算調制斜率所需的兩次FFT運算時可調用fft核實現。在調用fft核時,應考慮傅里葉變換的長度,采樣率越高脈寬越寬,所需的傅里葉點數越多,從而使用的資源越多。在設計前期因考慮FPGA所能適應的最大采樣率及最長脈寬,當超出資源時應適量減少傅里葉變換的長度,以測量精度換取資源。脈寬越長測頻精度越高,采樣率越高,能測量的瞬時帶寬越大,但同樣消耗的資源越多。計算信號的初始相位時可調用cordic核實現。信號恢復過程可用dds核或cordic核實現,碼元恢復過程僅需要少量的LUT邏輯門便可實現。縱觀LFM-BPSK復合信號參數快速估計及碼元恢復算法其主要消耗DSP48E硬件資源,輔以少量的LUT邏輯門便可實現,是一種硬件可實現的參數快速估計及碼元恢復算法。 為了驗證本文算法的有效性,做了如下仿真: 仿真中,碼元速率Cp=107,碼元個數N=63,信噪比SNR=-2:10 dB,步進為1。在此條件下,利用本文算法與文獻[10]算法分別做100次蒙特卡羅仿真,其碼元恢復的正確率如圖6所示。由圖6可看出,本文算法在信噪比大于0 dB時碼元的正確率為100%,可以完美恢復碼元,但文獻[10]所提供的算法無法正確恢復出碼元。基于以上情況,在SNR=10 dB時,查看文獻[10]的碼元恢復情況。由圖7可知,文獻[10]算法前20個碼元可以準確地恢復。但是,隨著碼元速率誤差的積累,使后面的碼元無法正確恢復。因此,文獻[10]所提供的算法無法支撐長碼恢復,而本文算法無此限制。 圖6 不同算法碼元恢復的正確率 圖7 SNR=10 dB碼元恢復 基于LFM-BPSK復合信號的特點,本文先利用平方運算將復合調制信號參數估計轉換為單一線性調頻參數估計,恢復線性調頻信號,與原信號共軛相乘,恢復相位編碼基帶信號,對編碼信號進行參數估計及碼元恢復。通過第2節的理論分析及第3節的仿真,本文提出的算法可利用硬件快速實現并達到良好的碼元恢復效果,是一種工程可實現算法。但是,此算法在參數估計中涉及了平方運算,造成信噪比降低,因此在利用此算法之前應用時域、頻域濾波或其他積累算法提高信號的信噪比。
2 算法原理

2.1 LFM參數快速估計




2.2 復合信號初始相位估計



2.3 BPSK碼元速率估計



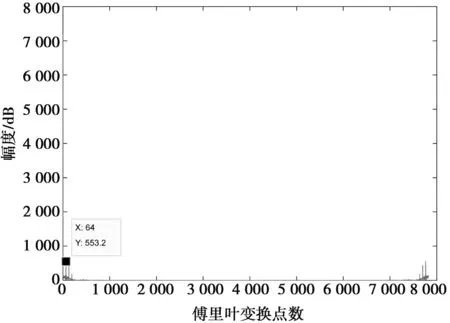
2.4 BPSK碼元恢復




3 性能分析
3.1 硬件可實現分析
3.2 仿真結果


4 結束語

