地下水動力學課程中的基礎數學運用

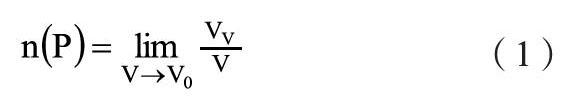
[摘 要]在地下水動力學教學過程中，發現不少學生存在數學基礎不夠扎實的問題，在學習這門課程時，很難與學過的數學知識聯系。據此，通過將教材中用到的數學知識進行系統的梳理，主要包括基本方法、基本理論、數學模型及其求解三部分，期望對學生或從事該課程教學的教師有所幫助。

[關鍵詞]地下水;水文地質;動力學;數學;基本原理

[基金項目]河北地質大學2018年度校級教學發展與改革實踐項目“地下水動力學課程教學資源庫建設”（2018JF06）

[作者簡介]王超月（1988—），男，博士，河北地質大學水資源與環境學院講師，主要從事水文地質學理論與教學研究。

[中圖分類號] G640[文獻標識碼] A[文章編號] 1674-9324（2020）45-0-04[收稿日期] 2020-06-12

地下水動力學是地下水科學與工程、水文與水資源工程、地質工程等專業本科生的一門基礎理論課。其先修課程有高等數學、普通地質學、水文地質學基礎、水力學等。它是地下水科學或水文地質學工作者必要的知識儲備，也是地下水數值模擬的理論基礎。課程主要講述了地下水運動的基本原理以及計算方法。該課程的特點是用到的數學知識多，理論性強，并且具有鮮明的實際應用背景。

筆者仔細翻閱了《地下水動力學》[1，2]以及《高等數學》[3]等教材，并結合多年授課經驗，梳理了課程中主要的數學知識點。其中也涉及筆者對一些基本概念的理解，有不當之處，懇請讀者給予指正。

一、基本方法

與高等數學純數學相比，作為專業課，多了實際背景。差別首先體現在變量符號的使用上。數學里通常用y表示因變量，x表示自變量。而在地下水動力學課程中，各物理量均有實際的物理意義，x，y，z用來表示空間自變量，t表示時間自變量，H，p，v分別表示地下水水頭、壓力、滲流速度（來源于相應英文單詞首字母），它們是時空變量的函數，如H（x，y，z，t）。各物理量所用符號一般與國內或國際慣例一致。這也方便了后期深入研究以及學習外文著作。

（一）極限與導數

1.極限。為了宏觀上研究地下水，提出滲流理論，引入了典型單元體（或典型體元，REV）的概念，假想水流充滿整個空間，不考慮巖土顆粒的存在，使得孔隙度（n）、水頭（H）、水壓（p）以及滲流速度（v）等在任意點P（x，y，z）處都有恒定的值，并且空間上具有連續性。典型單元體是使取樣平均性質穩定的最小體積，在宏觀上其值很小，可以想象其包含有限顆粒（如1000個）。如任意P點孔隙度定義為

含義即為在含水層中以P點為中心，取樣體積逐漸減小至典型單元體時，計算的孔隙體積與土樣體積的比值。

2.求導運算。課程中涉及的求導公式一般為簡單的四則運算，如地下水的狀態方程中：

二、基本理論

（一）特殊函數

教材上涉及的特殊函數主要有兩類，一類是在數學上普遍應用的，在數學手冊上可以查到具體表達式，如Bessel函數、虛宗量Bessel函數、（余）誤差函數、伽馬函數、雙曲函數等。另外一類是在水文地質方面特有的函數，如井函數W（u）、不考慮弱透水層彈性釋水時越流系統的井函數W（u，r/B）、考慮弱透水層彈性釋水時越流系統的井函數H（u，β）、無壓含水層中完整井的井函數W（ua，y，r/D）等。它們均具有特定的表達式，可以做成數據表，利用配線法反求水文地質參數時，被用作標準曲線。

（二）極值與最小二乘法

在尋求實際抽水流量與降深關系時，可以嘗試經驗公式。求解思路是找流量—降深的“線性關系”。將觀測數據畫到坐標圖上，首先觀察Q-sw是否呈線性關系，若不是，觀察～Q，lgQ～lgsw，Q～lgsw是否呈線性關系，即分別對應流量與水位降深關系為直線、拋物線、冪函數曲線以及對數曲線幾種常用形式。確定曲線類型后，可以利用最小二乘法求得未知參數。最小二乘法屬于函數微分的應用，殘差平方和（目標函數）最小時的待定系數即為最優參數。求最小值時令目標函數的導數或偏導數為零，通過求解方程或方程組最終得到最佳擬合參數。實際應用時可以通過EXCEL添加趨勢線的方式獲得最佳參數。

（三）梯度與水力坡度

由于地下水流場的連續性，水頭H（x，y，z）在任意點P（x，y，z）具有連續的偏導數，梯度即為

一致。y是關于x的函數，是關于的函數，a、b是常數，所以曲線的形狀與y-x曲線的形狀完全相同，只是沿水平方向上平移了a，沿垂向上平移了b。需要注意的是，Theis公式的配線法是在雙對數坐標下的。因此，需將觀測數據繪制于與W（u）-1/u標準曲線相同模數的雙對數坐標紙上，兩曲線重合后，取任意匹配點，讀取相應兩組坐標值，帶回公式，即可求導水系數T與貯水系數S。

（五）張量

向量可以表示有方向和幅度的物理量，比如力、加速度。各向同性介質的滲透系數是一個標量，而各向異性介質的滲透系數較復雜一些，任意點的滲透系數與方向有關，用向量不能夠表示。這時需要用張量表示滲透系數，在三維空間里，滲透系數是2階張量，含32個數字，是3×3的矩陣。

張量是向量的拓展，向量是1階張量，同一物理量不同的張量形式，可以看作是不同坐標系下的線性變換。幸運的是，在一般介質中，總存在相互垂直的三個主方向上的滲透系數，可以用K1，K2，K3表示，當介質的滲透系數主方向與我們所選坐標系三軸分別平行時，此時滲透系數張量變為對角矩陣，滲透流速計算大大簡化，，，。而介質滲透系數主方向與坐標系三軸方向不一致時，可不可以把坐標系改一下呢？我們在研究某個問題時，坐標系往往已經確定了，即水平方向上是x軸、y軸，垂向上是z軸，這也是我們計算水頭以及水力坡度的依據，坐標系的位置不能僅考慮介質的需求。此時，K1，K2，K3依然是介質三個主方向上的滲透系數，只不過與坐標軸不重合，為了計算滲流速度，需要采用滲透系數張量的一般形式。

三、數學模型及其求解

（一）模型假設

數學模型的建立均基于各種假設，這些假設也是其應用的前提。模型假設是普遍存在的，假設的提出往往極大地簡化了實際問題，最終服務于問題的解決。

如Dupuit假設的提出使潛水面邊界問題的處理簡單化。假設潛水面比較平緩，等水頭面鉛直，水流基本上水平，可忽略速度的垂直分量，同一鉛直剖面各點的水力坡度和滲透速度相等，使三維問題（x，y，z）降階為水平二維（x，y）問題處理;使剖面二維流問題（x，z）降階為水平一維問題近似處理;Dupuit假設使潛水面邊界直接近似地在微分方程中處理。該假設忽略了滲流速度的垂直分量，然而，在垂向分速度較大的地段，則不能采用。

又如在推導承壓水運動的基本微分方程時，假設：（1）水流服從Darcy定律;（2）K不隨ρ=ρ（p）的變化而變化;（3）Ss和K也不受n變化的影響;（4）含水層側向無壓縮，只有垂直方向的壓縮，于是得到各向同性介質中承壓水非穩定運動的基本微分方程：

除以上假設外，還假設：（5）水基本上是垂直地通過弱透水層，在主含水層中基本上是水平流動的;（6）忽略弱透水層本身釋放的水量。另外，該方程實際反映的是承壓含水層的平面二維運動。

（二）偏微分方程與定解條件

1.偏微分方程。高等數學中只有偏導數以及常微分方程的知識，對沒有學習過數學物理方程等相關課程的學生，初次遇見偏微分方程可能引起學生的恐慌。因此，課程教學中需要向學生說明偏微分方程的特點。如承壓水非穩定運動的偏微分方程（26）是二階偏微分方程，H是關于時空變量x，y，z，t的函數。滲透系數K當在括號內的時候，表示可以是隨空間變化的，即K（x，y，x）表示非均質介質。

2.定解條件僅給出偏微分方程，只能描述水流的一般規律，還不能確定具體的運動狀態，該方程也稱為泛定方程。如果附加一些條件后，就能完全確定具體運動狀態，稱這樣的條件為定解條件。表示開始情況的附加條件稱為初始條件，表示在邊界上受到約束的條件稱為邊界條件[4]。偏微分方程與定解條件一起構成數學問題或者數學模型，能夠得到確切的解。在高等數學中，類似有常微分方程的定解問題

只不過這里變成了偏微分方程，增加了變量。偏微分方程與定解條件構成“方程組”，在滿足解的存在且唯一的條件下，最終求解出H（x，y，z，t）。

3.柱坐標變換。在均質各向同性含水層中抽水時，形成的地下水降落漏斗中心對稱，通過采用柱坐標變換，可將空間三維流問題降階為二維流問題，大大降低了模型的求解難度。

（三）微分方程的求解

課程中二階常微分方程的定解問題求解相對簡單，如河渠間地下水的穩定運動，地下水向完整井的穩定運動等。二階偏微分方程的定解問題略微復雜，不同院校對本科生的要求可能不同。總體上講，教材中有推導過程的數學模型，如河渠間地下水的非穩定運動數學模型的線性化、承壓含水層完整井流Theis公式的推導等，容易理解些，讓學生學習一些數學模型的推導方法也十分有益。其他一些比較復雜模型，如：定降深井流計算;有越流補給的完整井流;有弱透水層彈性釋水補給和越流補給的完整井流;潛水完整井等的解析解推導過程一般涉及比較復雜的積分變換及逆變換，對于沒有學過復變函數與積分變換、數學物理方程等相關課程的同學往往有很大困難，可根據個人興趣，查找相關文獻學習。

（四）疊加原理

對于由線性偏微分方程和線性定解條件組成的定解問題，可以運用疊加原理。疊加原理在教材中多次用到，如河渠水位變化時，河渠間地下水的非穩定運動;地下水向干擾井群的穩定運動;均勻流中的井;階梯降深抽水試驗;流量變化時的Theis計算公式;水位恢復試驗;地下水向邊界附近井的運動;不完整井的運動等。

對于未知函數和它的各階偏導數都是線性的方程稱為線性偏微分方程。如

為線性偏微分方程。當右端f（x，y）=0時，方程叫作齊次的。

在高等數學中有類似定理：如果函數y1（x）與y2（x）是方程的兩個解，那么y=C1y1（x）+C2y2（x）也是方程的解，C1、C2是任意常數。該定理推廣到偏微分方程同樣適用。關于疊加原理的更多介紹可參考Jacob Bear的專著[5，6]。

四、結語

雖然在教材中涉及的數學知識比較多，但基本都是數學中比較基礎的內容。教學過程中，應針對學生可能的薄弱環節重點講解。教學中還應盡量借助軟件技術、數值方法、編程技術等，使理論的知識“活”起來，比如增加動態或者立體展示，增加學習過程中的可操作性。另外，課程中的一些經典推導可以培養學生的數學思維。需要指出的是，雖然隨著科技的進步，數值模擬技術日益成熟、精進，但數值模擬技術的熟練運用依然有賴于扎實的理論知識。更重要的是，數學作為學習和研究現代科學技術必不可少的基本工具，借此課程強化學生的數學思維、提高數學素養具有重要意義。

參考文獻

[1]薛禹群，吳吉春.地下水動力學[M].北京：地質出版社，2010.

[2]陳崇希，林敏.地下水動力學[M].北京：地質出版社，2011.

[3]同濟大學應用數學系.高等數學[M].北京：高等教育出版社， 2002.

[4]《數學手冊》編寫組.數學手冊[M].北京：高等教育出版社， 1979.

[5]Bear，J.Hydraulics of Groundwater.McGraw-Hill Publishing，New York，1979.

[6]Bear，J.Dynamics of Fluids in Porous Media.Dynamics of Fluids in Porous media.American Elsevier Pub.Co.，1972.

The Application of Basic Mathematics in the Course of Groundwater Dynamics

WANG Chao-yue

（School of Water Resources and Environment， Hebei GEO University， Shijiazhuang， Hebei 050031， China）

Abstract： In the course of Groundwater Dynamics teaching， it is found that many students have the problem that the mathematical foundation is not solid enough. During the study of this course， it is difficult for students to connect with the mathematics knowledge they have learned. For this reason， the mathematics knowledge used in the textbooks are summarized systematically. It mainly includes basic methods， basic theories， mathematical models and their solutions. It is expected to be helpful to the students or teachers engaged in the course.

Key words： groundwater; hydrogeology; Dynamics; mathematics; basic principles