多特征加權指數熵在光斑中心定位中的應用

張明富 馬月輝 段夢琨 鄭軍飛 孫曉賢

摘 ?要： 激光光斑中心檢測是視覺測量中常用的關鍵技術，檢測算法的優劣直接影響了測量的精度。針對現有光斑定位算法存在定位精度低、抗干擾能力差等問題，提出一種改進的激光光斑中心定位算法。該算法在Shannon熵的基礎上引入指數熵，并根據光斑圖像特征選取類內離散度最小和灰度對比度最大對指數熵進行加權處理，將使加權指數熵值最大時的灰度值作為閾值對光斑圖像進行閾值分割，由此消除噪聲干擾，最后由質心法進行光斑中心定位。實驗表明，在兼顧穩定性的同時，與傳統閾值分割方法相比，光斑中心定位誤差降低了22%以上。

關鍵詞： 視覺測量; 光斑定位; 指數熵應用; 閾值分割; 加權處理; 噪聲干擾消除

中圖分類號： TN911.73?34; TP391.41 ? ? ? ? ? ? ? ?文獻標識碼： A ? ? ? ? ? ? ? ? 文章編號： 1004?373X（2020）23?0020?04

Abstract： Detection of laser spot center is a key technology commonly used in vision measurement. The quality of detection algorithm affects the accuracy of measurement directly. In allusion to the problems of low positioning accuracy and poor anti?jamming ability of the existing spot location algorithms， an improved laser spot center positioning algorithm is proposed. The exponential entropy is introduced on the basis of Shannon′s entropy. According to the characteristics of the light?spot image， the exponential entropy is weighted by choosing the smallest intra?class dispersion and the largest gray contrast ratio. The gray value of the maximum weighted exponential entropy is used as the threshold to segment the spot image， and eliminate noise interference. The center positioning of the light?spot has been realized by the centroid method. The experiment results show that， in comparison with the traditional threshold segmentation method， the error of the laser spot center positioning algorithm is reduced by more than 22% while it gives consideration of stability.

Keywords： vision measurement; light?spot positioning; exponential entropy application; threshold segmentation; weighted processing; noise jamming elimination

0 ?引 ?言

基于視覺的形變測量系統具有精度高、非接觸、受環境影響小等優點，在橋梁、隧道等重點監測場合應用廣泛[1?2]。而大多數視覺測量系統選取亮度集中、抗傳輸介質干擾能力強的光斑作為待測物[3]，因此快速準確的光斑定位是實現精確形變測量的前提。

常用的光斑定位算法有插值法[4]、二維高斯擬合法[5?6]、灰度質心法[7]以及多種改進算法。插值法通常以光斑最亮點作為插值中心，選取插值中心[x]軸和[y]軸4個節點進行插值計算。插值法計算量小、運算速度快，但計算精度極易受所選插值節點灰度波動影響。對于邊緣含強干擾亮點的光斑圖，插值中心易誤選。二維高斯擬合法運算精度高，且穩定性好，對符合高斯分布的光斑圖具有較好的魯棒性。但其測量精度易受圖像具體分布和采樣數據樣本大小影響，在實際應用中往往需要對圖像和數據樣本大小進行具體分析。灰度質心法對于均勻光斑能夠精確定位，計算速度快，但抗噪能力差。直接光斑定位算法易受噪聲影響，對此文獻[8]采用先分割后定位處理光斑圖像，結果證實對干擾抑制較好。文獻[9]采用亮度閾值分割光斑圖，后運用圓幾何原理定位中心，算法簡單且計算速度快。文獻[10]對光斑圖像去噪校正后采用OTSU法進行光斑分割，最后采用插值計算中心，檢測結果穩定性優于對照算法。閾值法可有效消除噪聲干擾，提高定位精度，但對光斑圖進行閾值分割屬于小目標分割，其目標背景比通常小于0.1，在此情況下，現有的分割算法易引入誤差[11]，進而影響光斑定位精度。

由以上原因，本文采用先閾值分割后進行光斑質心定位，且考慮到光斑與背景灰度值相差較大，準確分割后光斑內部灰度均勻，類內方差很小等特點，可用來彌補最大熵法只考慮目標背景最大平均信息量，卻忽略圖像灰度分布以及目標背景差異性。基于此，本文將圖像灰度信息以及目標背景差異性作為權值對最大熵法進行加權處理，將加權指數作為光斑圖像閾值選取準則對圖像進行分割，以消除噪聲干擾并減少計算量，然后通過質心法進行光斑定位，使定位結果兼顧實時性與高精度。

1 ?信息熵閾值選取

1.1 ?最大Shannon熵閾值選取

1.2 ?最大指數熵閾值選取

當圖片灰度值[i]均存在，最大Shannon熵可快速準確選取最佳閾值。但對于光斑圖像，其背景與目標相交處灰度突變較大，由此可造成特定灰度值比例較少甚至缺失。此時若[pi→0]，則[ΔIpi→∞];若[pi=0]，則[ΔIpi=log（1pi）]無定義。因此，本文引入一種改進的自信息量表示，使得事件獲取的信息量滿足以下原則[13]：

2 ?光斑定位算法的改進

2.1 ?方差加權指數熵

指數熵可獲得更適合光斑特征的圖像最大平均信息量，但卻忽略了圖像灰度分布的重要性，由于激光光斑量集中，在最優分割后，光斑內部灰度均勻，在數學上表現為類內方差很小，可根據該特征對光斑指數熵進行加權。在1.1節圖像[i=fx，y]經閾值[T]分割后背景和目標平均灰度為[μ0]和[μ1]：

由于光斑灰度均勻，用其類內方差倒數對光斑信息熵進行加權，將使加權后的光斑信息熵遠大于背景信息熵，為減少運算量，方差加權指數熵閾值選取公式可簡化為：

2.2 ?多特征加權指數熵

將光斑類內方差作為權值計入其信息熵中，可以獲得考慮目標灰度相關性的最佳分割閾值。但圖像最小類內方差的計算依據是誤差平方和最小，在該準則下當不同類別包含個體數相差較大時，將大類分割開可能使誤差平方和更小。光斑圖像屬于小目標分割，其特征是目標背景之比通常小于0.1，將該準則應用于光斑最小類內方差選取，將背景劃分為光斑的一部分可獲得更小的類內方差，此時用類內方差對信息熵進行加權獲得更大的方差加權信息熵，造成光斑錯誤分割進而影響定位精度。

對于具有一定信噪比的光斑圖像，待檢測的光斑部分平均灰度一般明顯高于其背景平均灰度值，且灰度均值不受目標大小影響，基于此特性，為體現光斑與背景之間的灰度差異，引入光斑和背景平均灰度差作為權值來消除類內方差可能存在的誤分割。背景和目標平均灰度分別為[μ0]和[μ1]，考慮到目標背景所占比例，則式（11）方差加權指數熵可改進為：

3 ?光斑定位精度分析

3.1 ?高斯噪聲影響下光斑定位精度

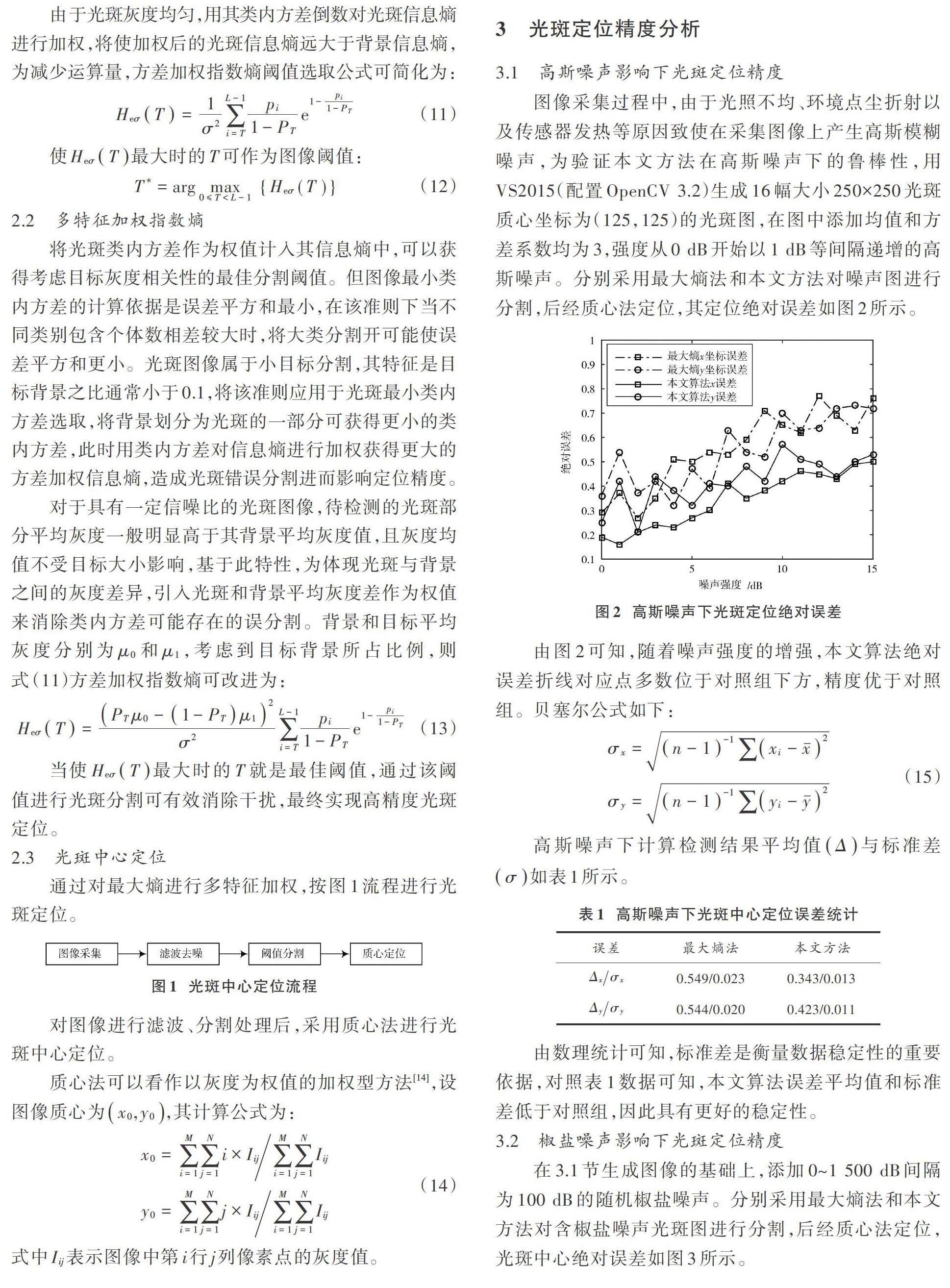
圖像采集過程中，由于光照不均、環境點塵折射以及傳感器發熱等原因致使在采集圖像上產生高斯模糊噪聲，為驗證本文方法在高斯噪聲下的魯棒性，用VS2015（配置OpenCV 3.2）生成16幅大小250×250光斑質心坐標為（125，125）的光斑圖，在圖中添加均值和方差系數均為3，強度從0 dB開始以1 dB等間隔遞增的高斯噪聲。分別采用最大熵法和本文方法對噪聲圖進行分割，后經質心法定位，其定位絕對誤差如圖2所示。

由數理統計可知，標準差是衡量數據穩定性的重要依據，對照表1數據可知，本文算法誤差平均值和標準差低于對照組，因此具有更好的穩定性。

3.2 ?椒鹽噪聲影響下光斑定位精度

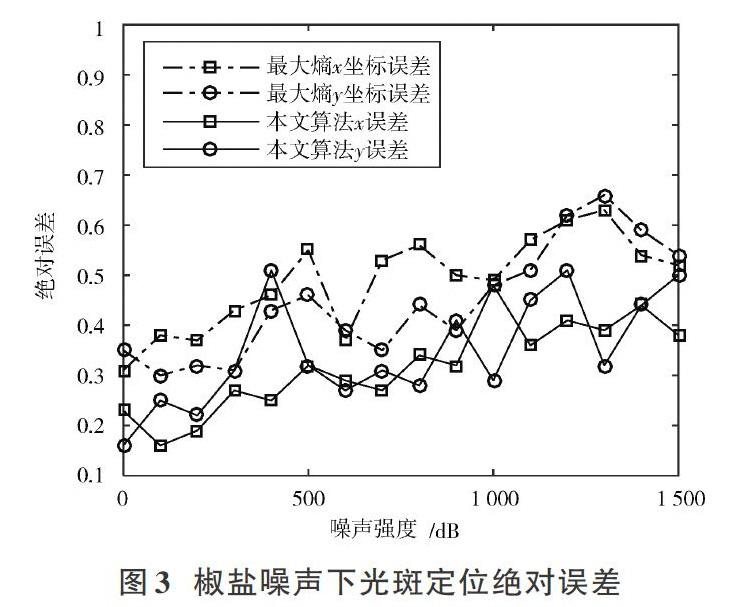
在3.1節生成圖像的基礎上，添加0～1 500 dB間隔為100 dB的隨機椒鹽噪聲。分別采用最大熵法和本文方法對含椒鹽噪聲光斑圖進行分割，后經質心法定位，光斑中心絕對誤差如圖3所示。

椒鹽噪聲下計算檢測結果平均值[Δ]與標準差[σ]如表2所示。

由表2數據可知：本文算法標準差小于對照組，具有更好的穩定性。對比平均誤差，本文算法誤差在[x]方向降低了35%，在[y]方向上降低了22%，在兼顧魯棒性的同時，提高了定位精度。

4 ?結 ?語

光斑中心檢測廣泛應用于視覺測量中，是視覺測量的關鍵技術，其定位精度直接決定了相關設備應用效果。本文將光斑灰度分布以及圖像目標背景灰度差異作為權值，對最大熵法進行加權，并將加權最大熵作為圖像閾值的分割準則，彌補了現有最大熵法對圖像灰度分布以及目標背景差異性利用不足等問題，提高了光斑定位精度。實驗結果表明，與對照組相比，本文算法抗干擾能力強，兼具穩定性與高精度。

參考文獻

[1] 劉兆蓉，王志乾，劉紹錦，等.激光光斑中心精確定位算法研究[J].計算機仿真，2011，28（5）：399?401.

[2] DONG Hongjun， WANG Long. Non?iterative spot center location algorithm based on Gaussian for fish?eye imaging laser warning system [J]. Optik?International journal for light and electron optics， 2012， 123（23）： 2148?2153.

[3] XU Yongfeng. A photogrammetry?based experimental modal analysis method by tracking visible laser spots [EB/OL]. [2019?08?20]. https：//www.researchgate.net/profile/Yongfeng_Xu.

[4] 張秋佳，趙玉華.基于加權插值算法的激光光斑中心檢測[J].激光與紅外，2016，46（1）：81?84.

[5] 陳和，楊志浩，郭磐，等.激光光斑中心高精度定位算法研究[J].北京理工大學學報，2016，36（2）：181?185.

[6] 郭晴晴，張運杰，李新，等.星載激光高度計地面光斑質心定位方法研究[J].量子電子學報，2018，35（3）：338?343.

[7] 席劍輝，包輝.基于改進質心法的激光條紋中心提取算法[J].火力與指揮控制，2019，44（5）：149?153.

[8] 徐亞明，束進芳，安動動.自適應閾值激光光斑中心定位方法研究[J].城市勘測，2014（4）：5?7.

[9] 郭玉靜，魏麗.一種基于亮度閾值的激光光斑中心定位算法[J].測試技術學報，2017，31（3）：223?226.

[10] 張紹堂，吳鴻，寧德瓊.一種高精度的激光圖像光斑中心檢測方法[J].激光雜志，2018，39（8）：153?156.

[11] 吳一全，吳加明，占必超.一種可有效分割小目標圖像的閾值選取方法[J].兵工學報，2011，32（4）：469?475.

[12] 吳一全，殷駿，畢碩本.最大倒數熵/倒數灰度熵多閾值選取[J].信號處理，2013，29（2）：143?151.

[13] 葛啟承，林錦國，肖迪.基于信息熵的圖像閾值選取算法[J].江蘇科技大學學報（自然科學版），2010，24（5）：485?488.

[14] 李朋，高立民，吳易明，等.加權質心法亞像元定位誤差研究[J].電子測量技術，2011，34（6）：43?46.