基于凸優化理論的和、差波束方向圖合成新方法

祁崢東, 邱明華, 蔣瑩瑩, 孔 玥, 黃 晟

(1. 中國船舶集團有限公司第八研究院，南京 211153 ；2. 南京大學 電子科學與工程學院，南京 210046 )

0 引 言

波束合成技術是陣列信號處理研究領域中的關鍵研究方向，其內容包括對接收陣列信號的加權處理，以使方向圖主瓣對準期望角，零陷位置對準干擾角，從而提高系統的性能。該技術在聲聲吶、雷達、通信等領域中得到了廣泛的應用，在方向圖綜合問題中通常要求具有低副瓣特性。通過各類算法，理論上[1-6]可以設計出具有超低副瓣電平的遠場方向圖。但是，由于仿真和實際加工存在各種誤差，如單元之間的互耦效應、單元位置加工誤差、通道響應失配，以及單元的幅相誤差等因素，提高了最大副瓣電平。此外，所設計的遠場方向圖應具有較好的方向性(如對應較窄的主瓣波束)。因此，綜合過程應在最大副瓣電平和主波束寬度之間進行平衡。和、差波束方向圖因在實現角度估計和目標跟蹤方面發揮著特殊的作用，使得這一研究方向一直以來受到很多學者的重視，目前已有很多技術成果問世。[7-11]

隨著軍民兩個領域對雷達分辨率、靈敏度等性能指標的要求不斷提高，使得雷達陣列朝著超大型規模發展。這一實際要求使雷達成本大幅提高，促使稀疏陣相關的研究得到越來越多的關注。稀疏陣的陣元合理的布置可以在不影響一些技術指標的前提下有效降低天線單元和通道總數,從而降低系統的造價和饋電網絡的復雜度。稀疏陣的單元位置優化和單元數量最少化問題實際屬于非線性優化范疇，以往經典解決方案包括采用智能優化算法、模擬退火法、遺傳算法、蟻群優化算法和粒子群算法等。作為高效的全局優化算法，智能優化算法已在陣列方向圖綜合領域得到大量應用，并取得了良好的應用成果[12-15]。但是，此類算法存在運算量大、易陷入局部最優、對初值敏感、收斂速度慢的缺點，尤其對大型天線陣列進行綜合優化時陣元單元數量的激增會導致算法的計算負擔增大。

稀疏陣綜合的目的為使得陣列中單元數量最少化，即完成方向圖性能指標的同時從等間距柵格的滿陣中選擇數量最少的單元。此問題為L0范數最小化綜合問題，為NP-Hard困難問題。本文結合壓縮理論用重加權L1范數優化算法替代原先L0范數算法以完成陣元數量最小化的設計目標。這一過程將非凸優化模型轉換成凸優化(Convex programming)模型求解。

本文提出的以降低饋電系統復雜度為目的設計可分為兩類，第1類是通過優化使得和、差波束模式下在部分單元上共用激勵，第2類降低系統復雜度的方法是通過減少天線陣列中單元總數。本文算法將共用單元部分加權和單元級加權作為統一優化目標，以減少陣列中單元總數，而將涉及的輻射性能指標(如差方向圖斜率，以及和、差波束的主瓣寬度、最大副瓣電平等)利用凸優化算法轉化為凸問題進行求解。

與經典算法結果相比，本文基于L1范數最小化的稀疏陣綜合方法與凸優化方法相結合的算法在提高某些方向圖輻射性能的同時可以有效減少陣列中單元的個數，從而有效簡化饋電網絡。

1 算法應用模型

1.1 遠場方向圖模型

這里以平面陣列模型為例介紹本文算法，考慮2M×2N元的矩形陣列，其中沿x軸布置2M行單元，沿y軸布置2N行單元。各陣元等間距排布，dx和dy分別表示沿x軸和y軸陣元間距，遠場方向圖這里表示為

(1)

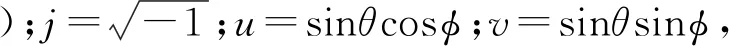
a=[a1，1,a1，2,…,a2M，2N-1,a2M，2N],

w(u,v)=ejβ[(-M+1/2)du+(-N+1/2)du]

=ejβ[(-M+1/2)du+(-N+3/2)du],…,

=ejβ[(M-1/2)du+(N-3/2)du]

=ejβ[(M-1/2)du+(N-1/2)du]

遠場仰、方位差波束輸出分別為

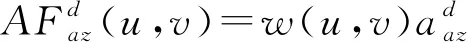
1.2 凸優化方法

本文將凸優化算法應用于和、差波束方向圖綜合問題，以期減少陣列中可變增益放大器和單元總數的同時提高方向圖性能，優化問題表述為

|w(u,v)as|≤ρs(u,v)(u,v)∈SLs,

|w(u,v)ad|≤ρd(u,v)(u,v)∈SLd,

(2)

這里，遠場和、差波束方向圖|AFs/d(u,v)|2的主瓣SBs/d以逼近期望和、差波形ds/d(u,v)為目的，這里有d(u,v)∈R+，其中，s、d分別表示和、差波數。|AFs/d(u,v)|2與ds/d(u,v)之間的距離εs/d盡可能地縮小。副瓣部分(SB)的峰值電平應該小于ρs(u,v)。式(2)中，控制和、差波束主瓣寬度的約束問題為非凸函數。本節對以往凸優化算法進行改進，引入雙變量的多凸優化算法，通過循環逼近的多凸模型來求解控制主瓣寬度的非凸問題，式(2)內容轉化如下：

(3)

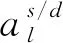
(4)

本節選擇文獻[16-19]中的基于迭代傅里葉技術獲得的滿足式(4)的陣元激勵權值作為迭代過程的初值。

1.3 迭代加權L1范數理論

本節將壓縮感知理論應用于單脈沖天線和、差波束合成技術中。為使陣列中單元總數盡可能少，稀疏陣列的綜合問題可表述為

(5)

式(5)為陣列中激勵值為0的單元數量。稀疏陣綜合的目的為使得陣列中單元數量最少化，即完成方向圖性能指標的同時從等間距柵格的滿陣中選擇數量最少的單元。此問題為L0范數最小化綜合問題，為NP-Hard困難問題。為解決此問題，利用重加權L1范數優化算法完成設計目標，可表述為

(6)

其中

和、差波束形成中共用陣元激勵的約束可表示為

(7)

式(7)是線性規劃問題。在迭代過程中，未知變量減少數量為Ψ個。 在迭代過程中，上一步的封閉解將作為下一步迭代的初值。陣列天線和、差波束的綜合問題在第n+1次迭代過程中激勵約束表述為

(8)

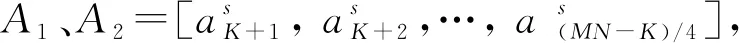
(9)

2 計算實例

為了驗證本文提出的算法，本節選擇文獻[10]中凸優化算法綜合得出的例1作為參考對比算例。

本節所有仿真驗證均采用臺式計算機，硬件參數如下：處理器：Intel? CoreTMi5-6500T，RAM為12 GB；仿真軟件為MATLAB，版本為R2018a。式(8)中μ值選擇固定值0.001。

例1中，初始陣列選擇口徑為5λ×5λ的正方形平面陣，且各陣元等間距排布，沿x軸和y軸陣元間距均為0.5556λ。設兩列共用單元，位置分布在{m=1,…,10,n=1,10}，即這兩列單元在和、差波束形成過程中共用激勵。圖1和圖2給出了本文提出算法得出的三維遠場方向圖，相應的陣元激勵與位置分布如圖3和圖4所示，僅畫出稀疏陣第三象限內的陣元分布和激勵值。綜合得出和波束的方向性系數值為19.03 dB，方位差波束斜率值為[?AFdaz(u0,v0)/?u]|u=u0,v=v0= 22.14 dB。

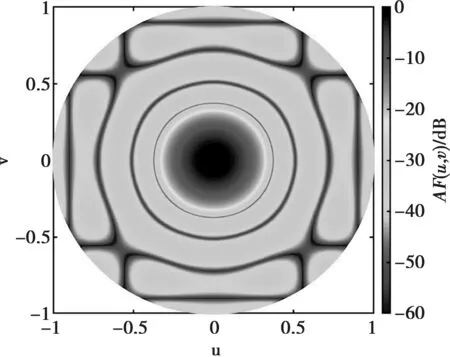
圖1 和波束三維方向圖的二維投影

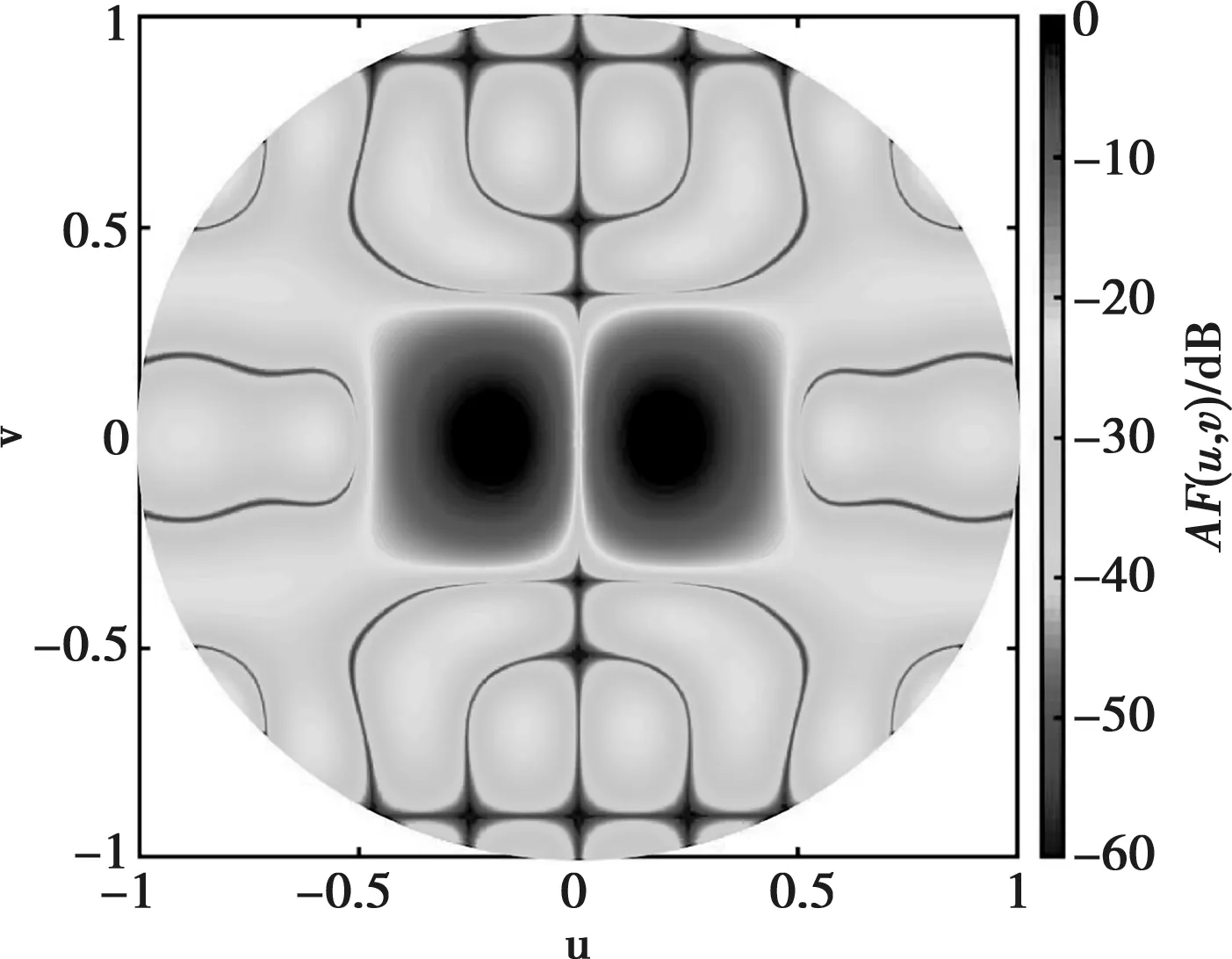
圖2 方位差波束三維方向圖的二維投影

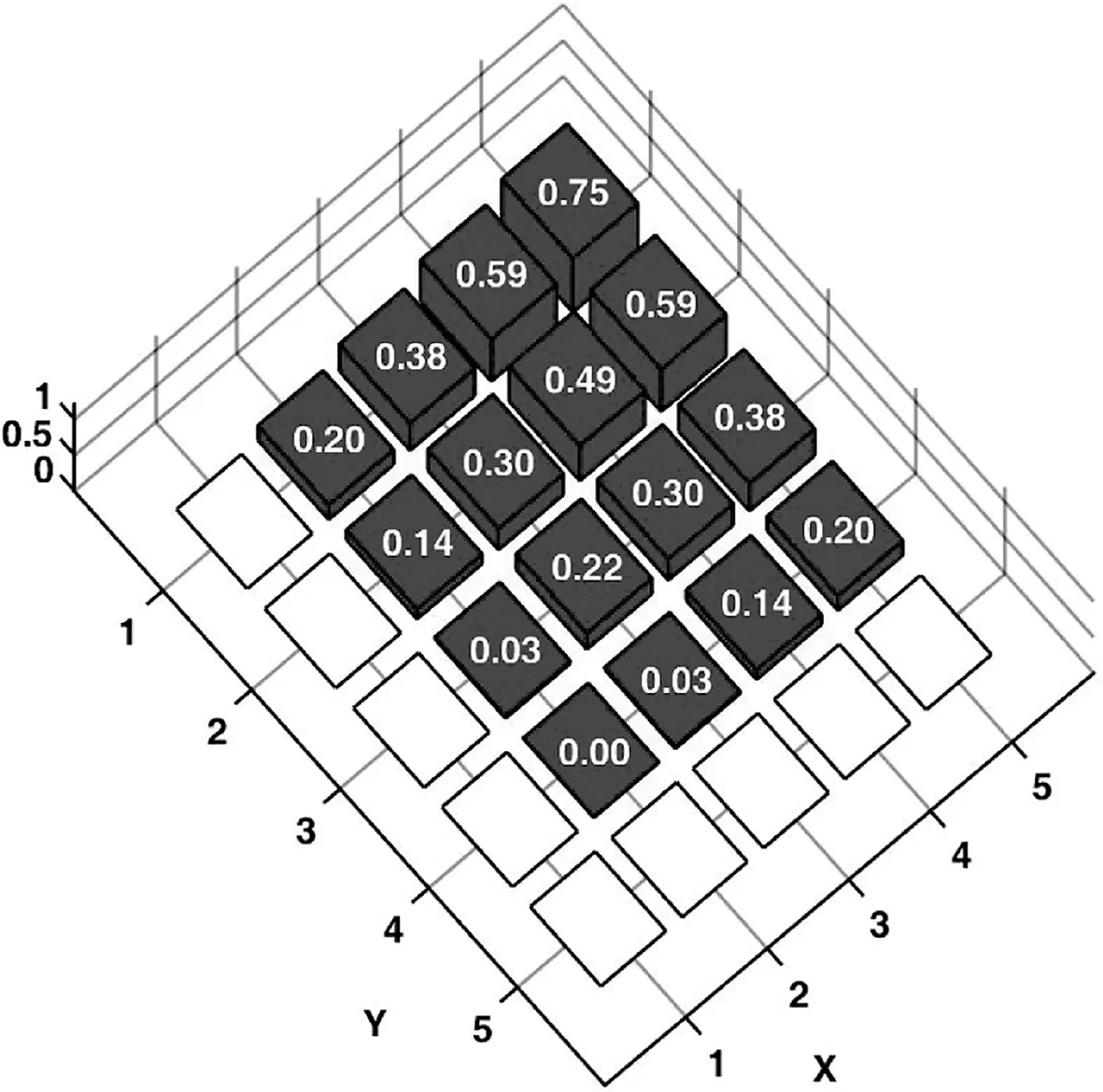
圖3 和波束對應激勵幅度

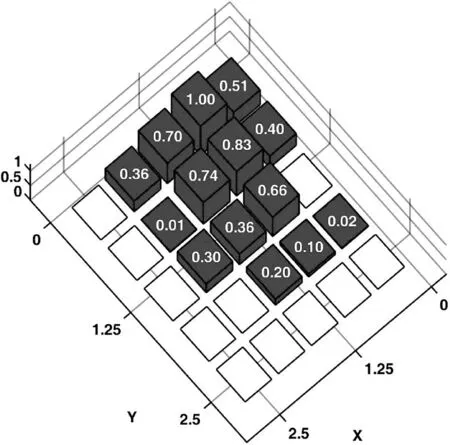
圖4 差波束對應激勵幅度

由表1中可以看出，和波束副瓣區域最高電平為PSLs=-32.8 dB，方位差波束副瓣區域最高電平為PSLdaz=-22.9 dB。綜合后的和、差波束在u=0、v=0方向上的半功率波瓣寬度(Half-Power Beamwidth，簡稱HPBW) 分別為HPBWPsu=0.27和HPBWsv=0.27，HPBWPdu=0.21和HPBWdv=0.27。與文獻[10]中LP算法綜合出的結果相比(如表1所示)，本文方法不僅實現了更低的最大副瓣電平(Peak Sidelobe,簡稱PSL)，并且獲得了更窄的波束寬度。與文獻[10]中的設計相比，本設計中“開”狀態的陣元數量在和、差波束兩種模式下分別減少了36% 和44%。此外，本設計中可變增益放大器(Variable Gain Amplifier，簡稱VGA)數量節省了30%，同時陣列孔徑減少了23.5%。

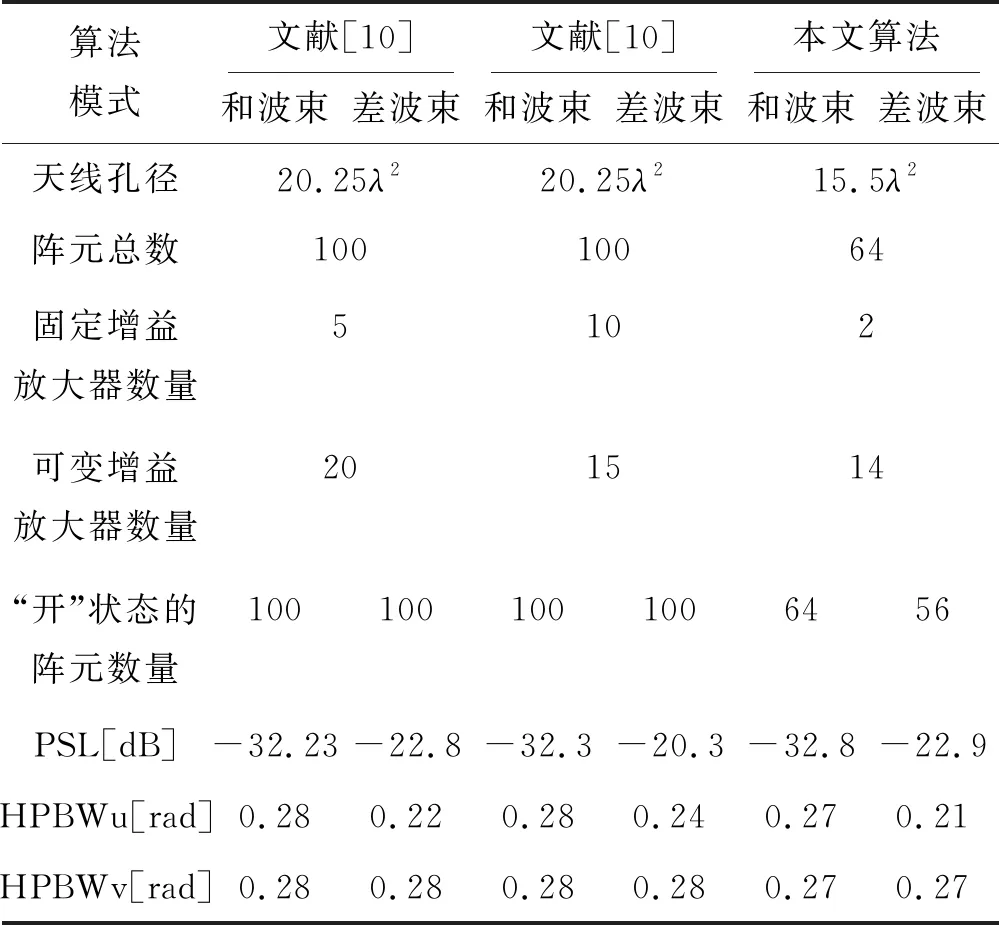
表1 本文算法與文獻[10]中LP算法的性能對比

例2中，初始陣列選擇口徑為5λ×5λ的正方形平面陣，且各陣元等間距排布，沿x軸和y軸陣元間距均為0.5556λ。設兩列共用單元，位置分布在{m=1,…, 10,n=1, 10}，即這兩列單元在和、差波束形成過程中共用激勵。 圖5和圖6給出了本文提出算法得出的三維遠場方向圖，相應的陣元激勵與位置分布如圖7和圖8所示，共用激勵用深黑色標記。綜合得出和波束的方向性系數值為19.23 dB，方位差波束斜率值為[?AFdaz(u0,v0)/?u]|u=u0,v=v0= 23.05 dB。由表2中可以看出，和波束副瓣區域最高電平為PSLs=-21.5 dB，方位差波束副瓣區域最高電平為PSLdaz=-16.5 dB。綜合后的和、差波束在u=0、v=0方向上的HPBW分別為HPBWPsu=0.27、HPBWsv=0.21、HPBWPdu=0.18和HPBWdv=0.23。與文獻[10]中LP算法綜合出的結果相比(如表2所示)，本文方法在實現了相同的最大副瓣電平值的同時獲得了更窄的波束寬度。與文獻[10]中的設計相比，本設計中“開”狀態的陣元數量在和、差波束兩種模式下分別減少了40%和44%。此外，本設計中VGA數量節省了45%。

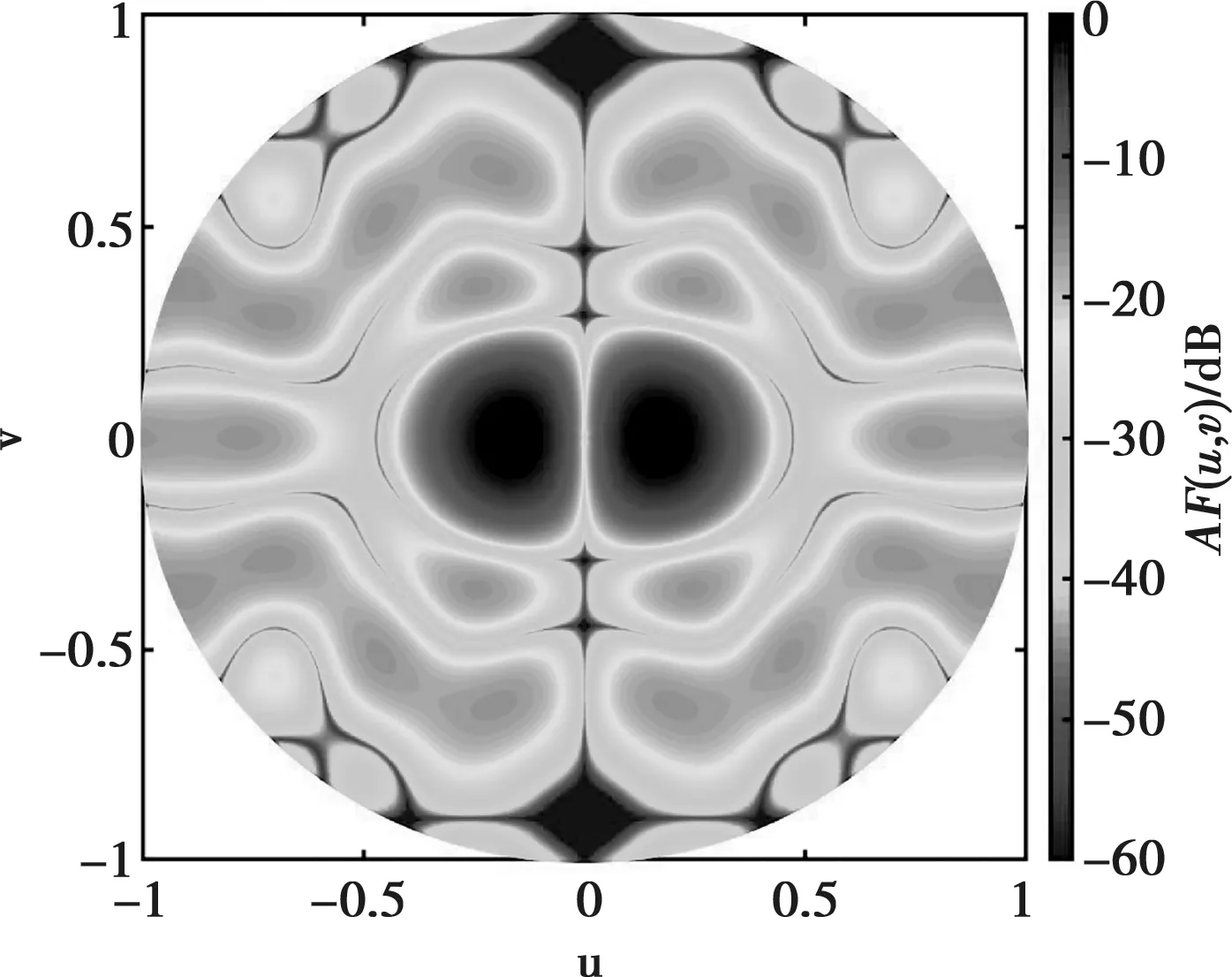
圖6 方位差波束三維方向圖的二維投影

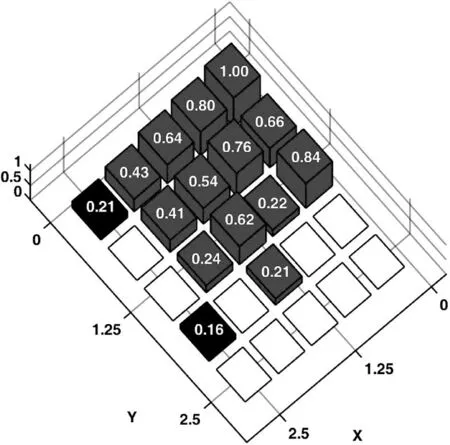
圖7 和波束對應激勵幅度

3 結束語

本文提出了一種采用凸優化算法與壓縮感知理論相結合的和、差波束方向圖合成新方法，將控制和、差波束的主瓣寬度的非凸約束問題轉化成凸約束問題進

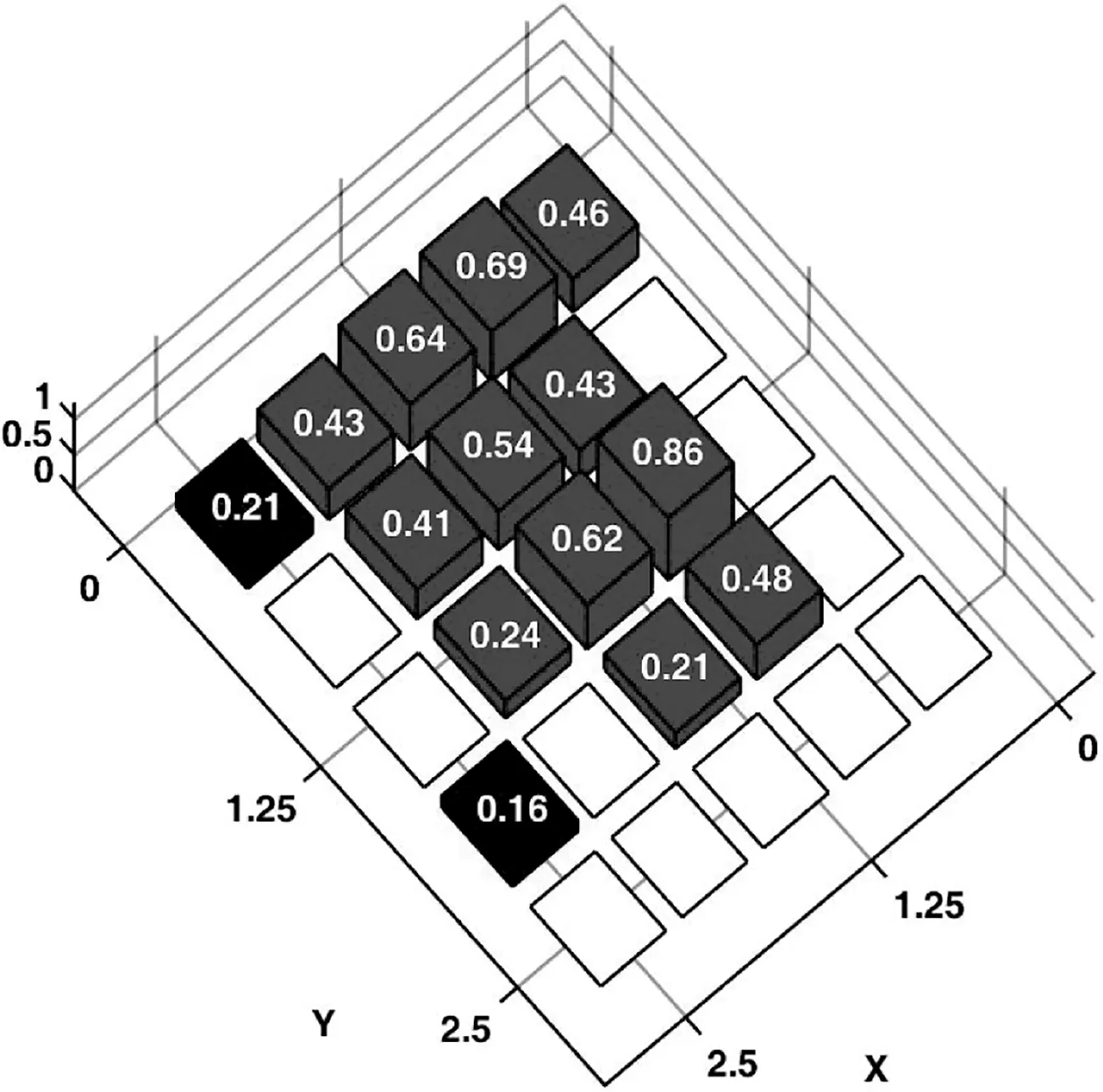
圖8 差波束對應激勵幅度

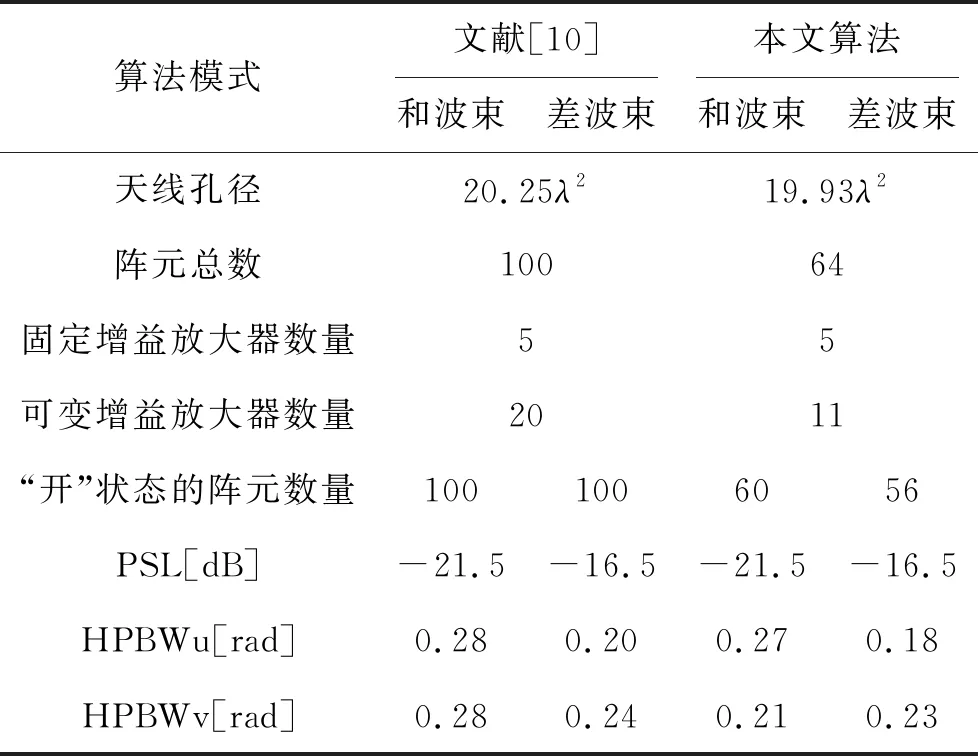
表2 本文算法與文獻[10]中LP算法的性能對比

行求解, 并結合壓縮理論用重加權L1范數優化算法替代原先L0范數算法以完成陣元數量最小化的設計目標。這一過程將非凸優化模型轉換成凸優化模型求解。本文提出的以降低饋電系統復雜度為目的設計可分為兩類，第1類是通過優化使得和、差波束模式下的部分單元共用激勵，而第2類降低系統復雜度的方法是通過減少天線陣列中單元總數。本文算法將共用單元部分加權和單元級加權作為統一優化目標，以減少陣列中單元總數。不同方向圖要求的稀疏平面陣綜合結果表明，與現有的和、差波束優化算法相比，本文算法具有很好的普適性，綜合得出的和、差方向圖性能更優且所需的陣列單元總數、可變增益放大器總數均更少。