泵站站內機組運行組合的優化研究
肖若富,龔詩雯,周玉國,張 斌,吳 榮
(1.中國農業大學北京市供水管網系統安全與節能工程技術研究中心,北京 100083;2.中國灌溉排水發展中心,北京 100054;3.寧夏自治區固海揚水管理處,寧夏 中寧 755100;4.寧夏自治區水利廳灌排中心,銀川 751000)
0 引 言
許多大型泵站都采用泵站群的調水方式,在運行過程中各級泵站的流量、揚程密切相關,各泵站機組型號、臺數不一,輸水線路長,沿途區間分水多,實際運行中通常根據經驗運行,效率低,能耗高[1]。由于機組容量高,運行時消耗的能量較大,因此,對于泵站站內運行需要進行科學、合理的機組運行組合優化[2]。
許多學者對于泵站系統優化調度問題展開了大量研究,Zessler等[3]針對一個八庫七泵站供水系統,運用動態規劃法通過逐步求解尋求到最佳的泵運行時間表,實現了運行成本最低。Lansey等[4]運用非線性網格仿真模型,并將泵運行臺數考慮在內,實現泵站運行費用最小,能耗最低。Ostfeld等[5]通過將蟻群方案與EPANET聯系起來,以系統設計和操作成本最小為目標,在滿足系統要求和用戶要求的情況下,以管道直徑,泵站最大功率和蓄水池容量,泵站水位和蓄水池水位為決策變量,并通過兩個抽水配水系統的基本運行測試該方案的可行性與靈敏性。Borkowski等[6]運用遺傳算法,在滿足系統要求、水位、流量的情況下,盡可能減少泵調速周期,同時參考能源價格,盡可能選擇耗能較少的泵機組運行。汪安南等[7]針對大型軸流泵站,采用逆序動態規劃法,以泵站運行費用最小為目標,確定泵站開機臺數、機組運行角度、和泵站最優運行曲線。劉正祥等[8]采用動態規劃和模擬技術相結合的方法,考慮級間的合理調配和站內機組的優化組合,針對多級泵站以能耗最小進行優化調度,取得了較為理想的結果。李世芳等[9]對梯級泵站,以機組能耗最小為目標函數,以調蓄水位為級間聯系變量,采用動態規劃法求解數學模型,使供水系統在最優狀態工作,提高了供水單位的經濟效益,具有良好的通用性。
通過以上研究可以發現,目前對于泵站系統優化調度問題求解方法包括:直接運用單一數學規劃模型來研究復雜提水工程的規劃調度;引入大系統優化決策模型、混合模型、計算機模擬技術、智能算法來研究復雜系統優化調度決策。本文通過建立單個機組及泵站的數學模型,以水位為決策變量,以泵站運行功率最小為優化目標,將粒子群算法與動態規劃法結合起來[10,11],求解目標函數確定各機組的運行工況,并對其進行理論分析,調整泵站站內機組的組合,實現泵站整體運行功率最小的目的。
1 研究對象
某多級提水工程共有泵站17座,安裝75臺水泵,其中主干有四級,東干有五級,西干有八級,各級還有支渠及蓄水池,且每級站泵型多在2~3種、水泵機組多在3臺以上。為了解決用水區域的缺水問題,該大型泵站從黃河抽水,各級泵站必須滿足沿途地區對灌溉和居民用水的需求。以該提水工程的總干二級泵站為研究對象,該泵站有N500-M9/675型號的泵2臺、N700-M14/701T型號的泵3臺、N800-M9/1028T型號的泵2臺,泵站基本情況如表1所示。
表1 泵站參數
2 模型建立與求解
2.1 泵站內機組運行的模型
單機組的運行工況不僅與水位、流量、型號等有關,還與機組的加工、運行時長及輔助設備有關,通常情況下,單機組的模型建立如下所述。
泵站運行時單機組的運行功率為:
P=ρgQH/1 000ηz
(1)
ηz=ηmηpηtηc
(2)
由水泵的性能曲線知,H與Q之間的關系為:
H=f(Q)
(3)
在泵站的運行中,我們關心的是H-Q特性曲線的高效區段,可用二次多項式插值進行擬合(其中-Q效率曲線也采用二次多項式插值),其中a、b、c為多項式系數:
H=aQ2+bQ+c
(4)
在泵站的優化運行中,不僅要考慮水泵的特性曲線,還需要考慮系統裝置的整體特性,即在克服凈揚程的基礎上,還要克服管路阻力,此時需要求得水泵機組的裝置特性曲線,如圖1、圖2虛線、公式(5)所示:
圖1 圖解法確定水泵工作點
圖2 水泵并聯運行工作點的確定
Hz=Hj+SQ2
(5)
在泵站中,需要把水從水源逐一送至各個用水區,而輸送過程中,各機組管道最終匯合至主輸水管道,這時輸水管道有一定的損失,故由泵站運行的原理可知,系統中泵站需要的揚程的表達式如下:
H需=H凈+S0Q2
(6)
H凈=H需-S0Q2
(7)
泵站中水泵機組的工作點可由機組的裝置性能曲線與泵站裝置性能曲線求出,即:
Hz=H凈+S0Q2
(8)
2.2 站內機組運行的模型求解
站內優化主要考慮以下幾個方面:
(1)流量在站內各機組間的合理分配。當泵站接到調水任務后,可根據站內各機組的實際情況,為其分配合適的流量,使得站內的能耗最少。同一泵站內,機組型號相同時可以平均分配流量,型號不同或者型號相同運行條件不同時,可在運行過程中根據計算結果進行分配。
(2)站內機組的優化組合。當站內有多臺機組共同運行,揚程和流量一定時,在對流量進行科學分配的基礎上,通過不同機組的組合,盡可能發揮各機組的優勢,實現站內的最優化。
(3)站內各機組運行的最優工況。泵站運行時,機組型號不同,運行的工況點不同;機組型號相同時,經過長期的磨損,機組性能發生改變。故對各機組的工況點重新進行確定是非常必要的。
(4)泵站內機組組合優化運行的數學模型。泵站提水流量、揚程已知,機組不可調時,會有多種組合方式,也會有不同的運行功率,通過建立數學模型及模型求解尋優可尋求到使泵站運行最經濟的組合,并求得機臺數、開機種類及流量的分配,以站內總功率最小為優化目標時,如下:
目標函數:
(9)
其中:
(10)
約束條件:
(11)
0≤n≤M
(12)
Hi=hi2-hi1
(13)
hi1min≤hi1≤hi1max
(14)
hi2min≤hi2≤hi2max
(15)
Ni≤Nimax
(16)
Nijmin≤Nij≤Nijmax
(17)
Qijmin≤Qij≤Qijmax
(18)
對于不同的多級泵站及泵站群,不同的優化準則,可根據實際情況,改變數學模型及約束條件。
3 優化結果分析
各型號的特性曲線采用二次多項式插值曲線擬合,如式(19)~(27),圖3~圖5:
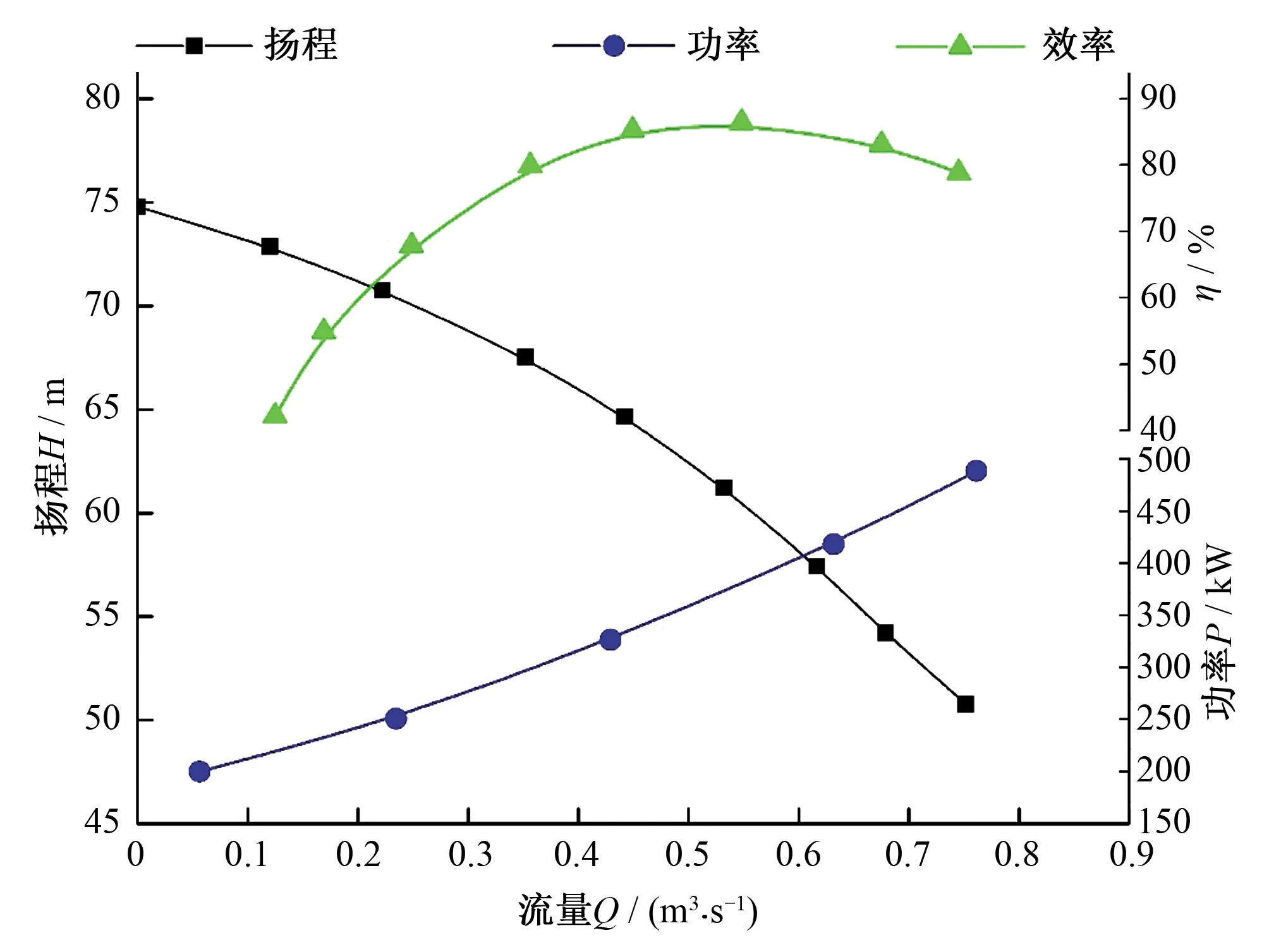
圖3 N500-M9/67性能曲線
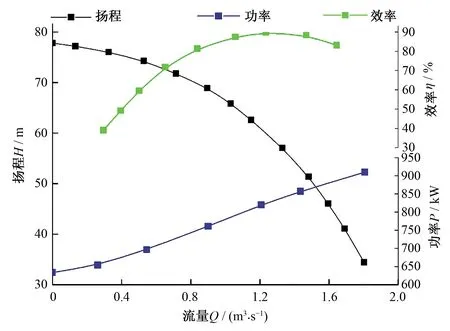
圖4 N700-M14/701T性能曲線
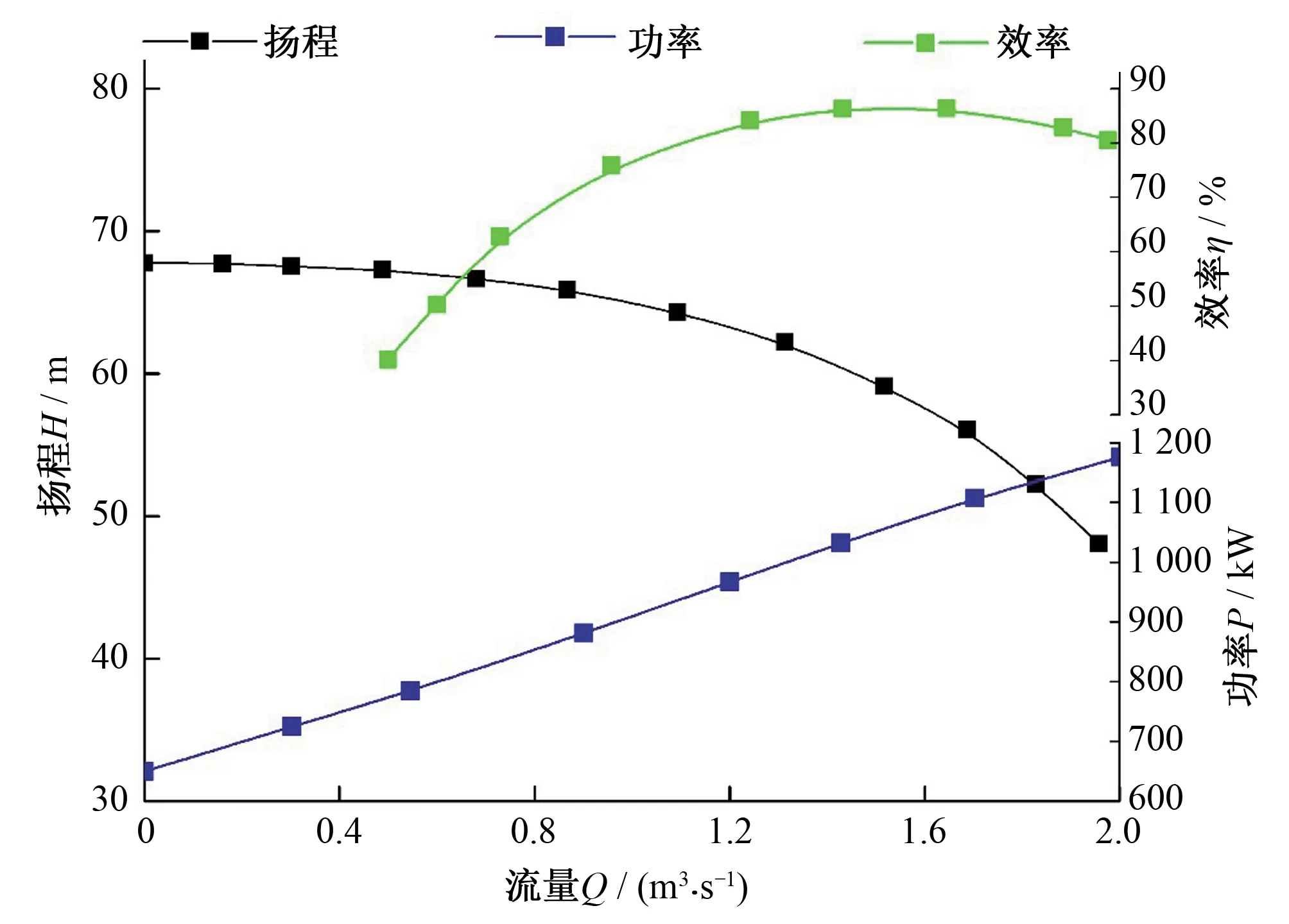
圖5 N800-M9/1028T性能曲線
N500-M9/675:
H=-28.84Q2-10.74Q+74.643
(19)
η=-2.477Q2+2.691 7Q+0.148
(20)
P=220.92Q2+229.04Q+185.91
(21)
N700-M14/701T:
H=-15.456Q2+5.104 2Q+74.79
(22)
η=-0.547 5Q2+1.38Q+0.372
(23)
P=1.485 1Q2+36.655Q+585.33
(24)
N800-M9/1028T:
H=-7.575Q2+5.826 8Q+66.915
(25)
η=-0.437 2Q2+1.334 8Q-0.136 5
(26)
P=2.805Q2+262.56Q+645.76
(21)
當該多級泵站及泵站群在用水區需水流量為6.1 m3/s下運行時,總干二級的運行情況為:總流量為6.1 m3/s,凈揚程為58.99 m,總揚程為60.8 m,3臺N700-M14/701T在設計工況點運行,流量為1.1 m3/s;2臺N800-M9/1028T,在設計點工況運行,流量為1.4 m3/s;而優化計算結果為:總流量5.8 m3/s,凈揚程57.02 m,總揚程60.385 m,1臺N500-M9/675,流量為0.54 m3/s,2臺N700-M14/701T,流量為1.21 m3/s,2臺N800-M9/1028T,流量為1.42 m3/s。兩者相比,優化后的結果更好,流量5.8 m3/s可以滿足用水區需求的流量5.78 m3/s,揚程也在限定范圍內,且用水區需水流量為6.1 m3/s時,實際運行消耗4 528 kW,優化結果消耗3 686 kW,節約了842 kW,可減少18.6%的損耗,優化效果顯著,泵站內機組可達到合理、高效的組合,可用于泵站的實際優化運行。
4 結 論
本文以某多級提水工程總干二泵站為研究對象,采用粒子群算法與動態規劃法的混合算法對總干二級泵站進行系統的優化。對于站內而言,以總干二級為例,通過優化使其機組組合情況發生變化,模擬計算得到泵站的運行情況,當泵站總運行流量為6.1 m3/s時,其抽水流量為5.8 m3/s,揚程為57.02 m,有5臺機組,3種不同型號的泵運行,優化后其單位運行時間內消耗3 686 kW,相對泵站實際運行情況節約了842 kW,節約了18.6%的能量。說明優化后的泵站在保證安全運行的前提下,得到了更優的調度方式,從而提高了泵站的運行效率,降低泵站整體運行的成本,節約能耗,最大程度地創造經濟效益和社會效益。
□

