毫米波網絡中基于Q-Learning的阻塞感知功率分配

施 釗,孫長印,江 帆

(西安郵電大學 通信與信息工程學院,西安 710121)

0 概述

在移動通信領域,頻譜資源是承載無線業務的基礎,是推動產業發展的核心資源。目前低于6 GHz的頻譜幾乎已經被分配殆盡,而6 GHz以上的頻譜資源非常豐富,由于其業務劃分與使用相對簡單,能夠提供連續的大帶寬頻帶,因此已成為一種具有前景的替代方案[1]。其中,高頻段的毫米波(millimeter-Wave,mm-Wave)通信更被認為是一種有效解決無線電頻譜稀缺問題的方法,將會為未來無線蜂窩網絡提供顯著的容量增益[2-4]。

目前,毫米波頻段將用于5G移動通信網絡已成為全球共識。在毫米波頻率下可提供的大帶寬有可能將網絡吞吐量提高10倍[3]。但是其面臨的信號衰耗大、覆蓋距離短和通信鏈路對阻塞敏感等問題也不可忽視[5]。克服這些問題的一種有效方法是增加接入點的密度[6-7],但是隨著接入點密度的增加,當所有毫米波基站重用相同的時頻資源時,小區間干擾會越來越嚴重,網絡管理的復雜度也越來越高[8-9],這將極大地限制毫米波小區的系統容量。對于毫米波信號衰耗大、覆蓋距離短的問題,可以通過波束成形技術進行最優波束對準,提高系統和速率。對于毫米波通信鏈路高阻塞問題,現場測量結果[3]表明,由于各種因素(如基站與其服務用戶之間的距離遠近、不同障礙物阻擋等)引起的阻塞,毫米波鏈路的可用性可能是高度間歇性的,這進一步惡化了超密集網絡由于復雜干擾導致的無線環境,對保證用戶業務質量帶來嚴重挑戰。

針對上述問題,研究者提出較多解決方案。文獻[8]通過使用Q-Learning算法,提出一種基于簇的分布式功率分配方案(Cluster based Distributed Power allocation using Q-Learning,CDP-Q)。該算法提升了系統容量,可滿足所有用戶所需的服務質量(Quality of Service,QoS),但未考慮毫米波通信的鏈路阻塞問題。文獻[10]方法通過協作Q-Learning算法來最大化毫微微蜂窩總容量,同時保證宏蜂窩用戶的容量水平。文獻[11]提出一種基于Q-Learning的下行鏈路容量優化資源調度方案,在保持宏小區用戶和毫微微小區用戶之間公平性的同時,提高小區邊緣用戶的吞吐量。然而,在文獻[10-11]中,毫微微用戶的QoS均未被考慮。文獻[12]考慮了毫米波多跳通信以克服鏈路阻塞,在直視路徑被障礙物阻斷時,通過中繼器繞開障礙物來提高可靠性,但這需要足夠高的節點密度以確保有合適的中繼節點可用。文獻[13]提出一種用于鏈路和中繼選擇的聯合優化算法。考慮到包括反射路徑的鏈接的阻塞概率,該算法選擇的鏈接將預期的交付時間最小化,但并未考慮多路徑的聯合使用,并且在基站用戶隨機分布機制下,一條路徑被阻塞時則需切換路徑,這種切換機制會引入額外的等待時間。文獻[14]建立一種基于波束的模型來評估毫米波覆蓋概率,其不僅考慮視距傳輸,而且還考慮了一階反射徑的影響。在非視距情況下,反射徑能夠顯著提高覆蓋率,但該模型未考慮系統容量的影響。

本文針對毫米波通信鏈路高阻塞可能引起中斷的問題,提出一種基于Q-Learning算法的功率分配方案。通過對鏈路阻塞問題進行分析,指出鏈路阻塞造成的影響有利有弊,因為鏈路阻塞有可能中斷有用信號,同時也可能會中斷干擾信號,其與基站、用戶的隨機分布以及周圍環境等因素有關。在此基礎上,將鏈路阻塞因素引入最優功率分配問題求解模型,借助利己利他策略[15]對利弊情況區別對待,并利用Q-Learning算法學習訓練利己利他最佳策略,從而減小干擾,提升系統總容量,同時為用戶提供所需QoS。

1 單智能體的Q-Learning算法

本節通過簡單案例介紹Q-Learning算法的基本概念[16]。Q-Learning是一種無模型的強化學習方法,其主要解決的問題是:一個能夠感知環境的智能體,通過與環境的交互反復學習,以狀態為行,以行為為列構建一張Q表來存儲Q值,根據Q值選取能夠獲得最大收益的動作。本文將此問題模型看作是馬爾科夫決策過程(Markov Decision Process,MDP)[17-18]。將MDP記為(A,S,Rt,St+1)元組,其包含以下元素:

1)智能體:執行學習行為并與環境交互的行為主體。

2)A={a1,a2,…,an}:一組智能體可能采取的有限的動作集合。

3)S={s1,s2,…,sn}:一組有限的狀態集合。基于t時刻的狀態st,智能體選擇動作at∈A。

4)Rt=r(st,at):智能體在t時刻、狀態st下執行特定動作at后的回報值函數,反映該動作的好壞,從而確定下一狀態St+1=Φ(st,at)。

5)St+1:獎勵被反饋給智能體,從而確定下一狀態St+1,并重復該過程,直至Q表不再有更新或者達到設定的收斂條件。

首先假定智能體處在某一環境下,并且它可以感知周邊的環境。其中,元素Q(st,at)就是在t時刻、st(st∈S)狀態下采取動作at(at∈A)所得到的最大累積回報值。

顯然,策略的好壞不是由一次學習過程的回報值所決定的,而是由長時間累積的回報值來決定,因此,定義評估函數為:

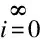
(1)

式(1)表示的是從初始狀態st不斷通過執行策略π進行學習獲得的累積回報值,其中,γ是折扣因子,γ∈[0,1],通過調節γ,可以控制后續回報值對累積回報值的影響,γ接近0表示智能體只在乎眼前的利益,做出的行為是為了最大化眼前的獎勵,γ接近1時表示智能體更看重長遠的利益,目的是使Vπ(st)最大化。

根據式(1)可以得出最佳策略π*為:

(2)

式(2)表示對于所有的狀態集合,使用策略π*可使累積回報值Vπ(s)達到最大。但在實際系統中,直接學習最佳策略π*是不切實際的[19]。使用評估函數來判斷動作的優劣更切合實際,評估函數定義如下:

Q(s,a)=r(s,a)+γV*(Φ(s,a))

(3)

由Vπ*(s)的定義和式(2)、式(3)可以得出:

(4)

將式(4)代入式(3)可得:

(5)

(6)

為控制之前學習效果對整體的影響,引入學習因子α(α∈[0,1]),其值接近0時表示幾乎不再進行新的學習,而接近1時表示更看重當前的學習效果,而且學習因子會影響Q-Learning算法收斂的速度。因此,Q函數更新為:

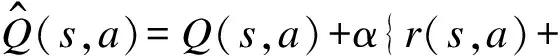
γ(Φ(s,a),a′)-Q(s,a)}=

(1-α)Q(s,a)+α{r(s,a)+

γ(Φ(s,a),a′)}

(7)

文獻[16]證明了這種更新規則在某些條件下可以收斂到最優Q值,其中一個條件是每個狀態-動作對必須進行無限次訪問。如上所述,Q-Learning在學習中獲得獎勵Rt,更新自己的Q值,并利用當前Q值來指導下一步的行動,在下一步的行動獲得回饋值之后再更新Q值,不斷重復迭代直至收斂。在此過程中,在已得到當前Q表的情況下,如何選擇下一步的行為對完善當前Q表最有利,即如何對探索和利用進行折中最為重要。為此,本文引入一個隨機因子ε來調節智能體進行學習的折中考慮,從而搜索到全局最優值并快速達到收斂。

由上述背景介紹可知,單智能體強化學習所在環境是穩定不變的,通常使用MDP來建模求解。然而,在多智能體系統中[20],每個智能體通過與環境進行交互獲取獎勵值來學習改善自己的決策,從而獲得該環境下的最優策略。在多智能體強化學習中,環境是復雜的、動態的,這給學習過程帶來很大困難。相比之下,對于單智能體面臨的維度爆炸、目標獎勵確定困難及不穩定性等問題,通常使用隨機博弈來建模求解。本文考慮這兩種方案的特點,針對網絡模型隨機分布即適合分布式解決方案的特性,選擇單智能體解決方案。

2 系統模型與問題描述

2.1 系統模型

本文基于5G典型場景之一的密集室外城市場景,考慮密集部署的毫米波基站下行鏈路。在網絡結構上,假設毫米波基站位置遵循基于密度λBS的泊松簇過程(Poisson Cluster Process,PCP)[21-22]。PCP在實踐中也被稱為父子建模過程,其包含一個父過程和一個子過程,父過程形成簇的中心,子過程圍繞父過程分布在簇中心一定的范圍。本文假設共有M個簇,每個簇有N個毫米波基站,每個基站僅服務一個用戶,用戶以基站為中心、以h為半徑隨機拋灑,且每個基站天線數為NT、用戶天線數為NR。假設單個小區邊緣用戶與其相關聯基站之間的距離大于設定界點距離d時有一定的概率會導致中斷,此時用戶的QoS會受影響,同時假定目標用戶在整個操作過程中保持靜止。

假設本文基站和用戶之間的信道模型為毫米波信道,基站i和用戶k之間的信道可以記為:Ii,k(d)×Hi,k。其中,Ii,k(d)是0-1布爾變量,表示基站i和用戶k之間的通信鏈路是否正常[23],d為設定的毫米波動態鏈路高阻塞引起鏈路中斷概率的界點距離。用PI(x)表示Ii,k(d)鏈路是否正常的概率。將毫米波基站與其相關聯用戶之間基于2D距離x的可視線概率記為PI(x),其由3GPP城市微街道峽谷模型[24]獲得,如式(8)所示:

(8)

其中,xi,k為當前毫米波基站i與其關聯用戶k之間的2D距離,當x≤d時,表示一定可視,鏈路無阻塞;當x>d時,表示有概率不可視,鏈路有概率被阻塞。

Li,k表示基站i和用戶k之間的路徑損耗,路徑損耗Li,k如式(9)所示:

Li,k=β1+10β2lgxi,k+Xζ

(9)

其中,β1和β2是用于實現最佳擬合信道測量因子,xi,k為當前毫米波基站i與其關聯用戶k之間的2D距離,Xζ～Ν(0,ζ2)表示對數陰影衰落因子。

此時第k個用戶的信干噪比(Signal to Interference plus Noise Ratio,SINR)為:

(10)

Pk=10(Pk′-Lk,k)/10

(11)

其中,Pk為第k個基站發送到其服務用戶k的實際功率,Pk′為Q-Learning算法中基站k選定某一狀態所執行的行為(功率),Lk,k為基站k到用戶k之間的路損,Dk為干擾基站的集合,σ2表示加性高斯白噪聲方差。因此,第Pk(Pk=Pk′-Lk,k)個用戶的歸一化容量為:

Ck=lb(1+SINRk)

(12)

2.2 問題描述

本文旨在毫米波基站之間尋找最優功率分配,為此,首先建立最大化問題模型,然后通過問題求解使系統總容量最大化,同時滿足所有用戶的QoS和功率約束。本文優化問題(P1)可以表述為:

(13)

s.t.

Pk≤Pmax,k=1,2,…,N

(14)

SINRk≥qk,k=1,2,…,N

(15)

其中:目標函數(式(13))表示最大化網絡總容量;M為系統模型中劃分簇的個數;N表示劃分的每個簇內的毫米波基站的數量;約束條件(式(14))指的是每個毫米波基站的功率限制,表示從每個毫米波基站分配給用戶的功率不能超過最大功率Pmax;式(15)中的qk表示第k個用戶所需的最小SINR值,稱為閾值。P1優化問題為:在使整個系統總容量最大的同時要滿足每個用戶所需的QoS。

由于P1優化問題中SINR項的分母包含干擾項,而在毫米波通信網絡中,干擾復雜不可忽略,因此,究其本質為一個耦合問題,此類優化問題是一個非凹函數,無法直接求解。傳統的啟發式方案所求得的僅為次優策略,與最優解誤差較大。而本文所要解決的是一個耦合問題,再加上考慮到毫米波鏈路阻塞特性導致的0-1布爾問題,使得P1更加難以解決,因此,本文考慮使用Q-Learning算法來解決此問題。

本文設計的P1的解決方案還具有以下特征:

1)由于設定場景為密集室外城市場景,毫米波基站和用戶數量眾多,干擾復雜多樣,沒有行之有效的中心管理機構,因此本文以分布式結構來處理。

2)毫米波通信雖然帶來了顯著的容量增益,但其信號衰耗大、輻射范圍有限,因此,合理假設只有距離接近的毫米波基站彼此干擾。可使用聚類機制將設定場景中的基站劃分為多個集群,其中一個集群的干擾對其他集群的用戶來說可以忽略不計。

3 PPCP-Q分配方案

本節介紹PCP網絡模型下基于Q-Learning算法的功率分配方案PPCP-Q。與其他強化學習算法相比,Q-Learning算法在復雜系統中具有非常好的學習性能。同時PCP還具有疊加性、稀釋性和映象性[19]等特性,非常適應毫米波網絡的復雜結構以及網絡環境的動態變化,因此,本文采用PPCP-Q方案進行功率分配。PPCP-Q算法分為PCP聚類和基于Q-Learning的分布式功率分配兩個部分。

3.1 毫米波基站的泊松簇過程

本文考慮系統模型具有分布式特性以及毫米波通信信號損耗大和覆蓋范圍較小的特性,假定在應用場景中只有距離靠近的毫米波基站之間彼此干擾。本文基于PCP假設將毫米波基站劃分為簇,PCP過程是一種分布式聚類方法,并可生成非重疊簇。為具體說明其過程,給出以下定義:

1)簇頭。基于PCP產生簇頭,在本文中,被選定為簇頭的毫米波基站與簇內其余毫米波基站之間沒有優先級之分。

2)入簇(In Cluster,IC)和簇外(Out Cluster,OC)節點。在PCP中,將IC距離定義為100 m,這是強干擾的表示。OC距離定義為200 m,其表示簇頭周圍簇的邊緣覆蓋范圍。若a點距某一簇頭在100 m范圍之內則定義為IC;若a點處于此簇的OC距離(即大于100 m小于200 m的范圍),而此時又不屬于任何其他簇的IC距離,則將a點作為OC節點加入此簇;若a點距離多個簇頭的距離相同,此時隨機選擇一個簇加入即可。

3.2 基于Q-Learning的分布式功率分配

Q-Learning算法是強化學習的典型方法之一,已被證明具有收斂性。在PPCP-Q算法中,毫米波基站被認為是Q-Learning算法的智能體。PPCP-Q是一種分布式方法,其中多個智能體旨在通過反復與環境交互來發現最佳策略(功率)以最大化網絡容量。

在多智能體的學習中,智能體可以合作學習(Cooperative Learning,CL)或獨立學習(Independent learning,IL)。在CL中,當前智能體與其他合作智能體共享其Q表。在IL中,每個智能體獨立于其他智能體學習(即將其他智能體視為環境的一部分,忽略其行為),雖然這可能導致算法收斂時間變長,但與CL相比,智能體之間沒有通信開銷,因此,本文選擇IL。PPCP-Q算法描述如下:

算法1PPCP-Q算法

輸入狀態集合,動作集合,學習因子α,折扣因子γ

輸出Q表

2.基于3.1節泊松簇過程對系統模型進行分簇

3.for所有簇

4.for每一個簇內智能體(毫米波基站)

5.for每一個智能體的訓練次數episode

7.生成一個0～1之間的隨機數sigma

8.if sigma<ε

9.ε=ε×0.99

11.else

13.end

16.根據式(7)更新Q表

18.end for

19.end for

20.end for

Q-Learning算法的輸出為分配的功率,被表示為Q函數,智能體的Q函數被稱為Q表,其中行是狀態,列是行為(功率)。在Q-Learning算法中,行為、狀態和回報函數定義如下:

1)行為。每個智能體可執行的動作是簇內毫米波基站可以使用的一組可能的功率。在仿真中,行為(分配的功率)集合A定義為A={a1,a2,…,an},它均勻地覆蓋了最小功率(a1=Pmin)和最大功率(an=Pmax)之間的范圍,步長為1 dBm。

(16)

其中,i,k=1,2,…,N。xi,k小于等于設定的界點距離d表示鏈路正常通信,此時為狀態0;xi,k大于d表示有概率導致鏈路中斷,此時為狀態1。

選擇一個簇,即A1、A2,利己利他策略應用示意圖如圖1所示。

圖1 利己利他策略示意圖Fig.1 Schematic diagram of egoistic and altruistic strategy

根據基站i與用戶k之間的2D距離xi,k,智能體在時刻t的狀態可分為以下3種情況:

情況1基站1與服務用戶1鏈路阻塞,基站1與被干擾用戶2、用戶3鏈路正常,即有用信號發生阻塞,用戶1考慮利他功率分配策略,此時應最小化發射功率,避免對其他用戶干擾。

情況2基站2及其服務用戶2鏈路正常,基站2與用戶1鏈路正常,與用戶3鏈路中斷,即部分被干擾用戶鏈路阻塞,此時應考慮利己利他功率分配策略,即按功率等級適量發射功率,均衡干擾同時提升系統容量。

情況3基站3及其服務用戶3鏈路正常,基站3與用戶1、用戶2鏈路中斷,即用戶3所產生干擾信號完全阻塞,此時應考慮利己功率分配策略,最大化發射功率,提升系統容量。

(17)

其中,k=1,2,…,N,A1和A2分別為10 dBm和5 dBm。

3)回報函數。本文優化問題P1旨在最大化系統總容量,同時滿足用戶所需的QoS。回報函數的設計基于優化目標,反映環境對智能體選擇動作的滿意程度。回報函數定義如下:

(18)

(19)

回報函數的基本原理如下:

1)只有當環境中毫米波基站最小和速率gt大于等于G倍的閾值時,才能得到一個正的回報值,否則回報值為負值。

2)因為(Ct-Glb(1+qk))/Ct<1,并且Ct越大,該值越大,所以系統吞吐量越大,對應回報值也越大。

此外,在學習過程中,需要設置一個隨機因子ε來調節智能體進行隨機學習的比例,本文假設隨機因子ε的初值為0.9,且智能體每進行一次隨機學習,該值就更新為原值的0.99倍。基于此設置,智能體在初始學習時會頻繁地進行隨機學習,隨著學習次數的增加和學習經驗的累積,隨機因子的值會逐漸趨近于0,此時智能體會進行經驗學習,選擇每一步的最優策略并快速達到收斂。

4 仿真與結果分析

本節對構建的系統模型進行系統級仿真,仿真程序在Matlab環境下實現,以證明本文方案的有效性。

4.1 仿真環境與參數設置

考慮密集部署的毫米波基站的下行鏈路網絡,在1 km2的區域內分布2個～16個簇。簇頭基于泊松過程生成,每個簇內基于半徑R范圍隨機分布N(N=5)個成員基站,依據成員基站與簇頭距離再劃分成員基站不重疊簇的歸屬。簇頭與簇內成員之間沒有優先級之分,且簇與簇之間相互獨立。簇內每個基站基于半徑h隨機拋灑一個用戶,即每個基站支持一個用戶。用戶的QoS被定義為支持用戶服務所需的最低SINR,所有用戶均考慮閾值qk=10 dB。在Q-Learning算法中,學習率為α,折扣因子為γ,最大迭代次數被設置為50 000次。其他仿真參數如表1所示。

表1 仿真參數Table 1 Simulation parameters

4.2 結果分析

本文基于PCP設定的系統模型基站和用戶的分布情況如圖2所示,圖中以不同形狀分別表示簇頭、簇內毫米波基站和相關聯的用戶。

圖2 PCP模型基站與用戶分布Fig.2 BSs and users distribution of PCP model

圖3所示為本文方案某個智能體在學習動作上的收斂情況。由于PPCP-Q方案考慮阻塞概率,使系統更加動態化,因此引入隨機因子ε對探索和利用進行折中考量,調節智能體進行隨機學習的比例,選擇集體最優而非單次最優的一串最優動作。隨著ε的值逐漸趨近于0,智能體會進行經驗學習,加快收斂速度。從圖3中可以看出,在前3 000次學習中,智能體進行了大量的隨機動作選擇,但是隨著迭代次數的增加,設定的隨機因子在逐漸減小,在3 000次～9 000次學習過程中隨機的動作次數逐漸減小,在9 000次學習之后,智能體在學習過程中動作的選擇逐漸達到收斂狀態。

圖3 Q-Learning算法動作收斂情況Fig.3 Action convergence of Q-Learning algorithm

將本文PPCP-Q方案與文獻[8]的CDP-Q方案進行比較,如圖4所示。可以看出,對于多種可能簇的大小,2種方案在系統總容量上的取值均超過閾值,均滿足用戶所需的QoS。圖5為PPCP-Q與CDP-Q兩種方案系統容量的CDF曲線對比。可以看出,PPCP-Q方案相較于CDP-Q方案提供了較為明顯的系統容量增益。增益機理分析如下:PPCP-Q方案考慮到毫米波鏈路可用性是高間歇性的,同時在Q-Learning算法狀態和回報函數設計中加入利己利他策略來求解目標函數,對有利有害情況區別對待并加以利用,在減小干擾的同時合理分配功率以最大化系統容量,同時滿足用戶的QoS。而文獻[8]的CDP-Q方案基于Q-Learning算法來訓練智能體分配功率,其采用利己分配策略,但未根據毫米波通信鏈路阻塞特性施加不同功率分配策略,所以在系統性能角度上,其增益受到限制。總體而言,本文方案顯著提升了系統容量,而且隨著簇的個數增多,性能優勢更為明顯。

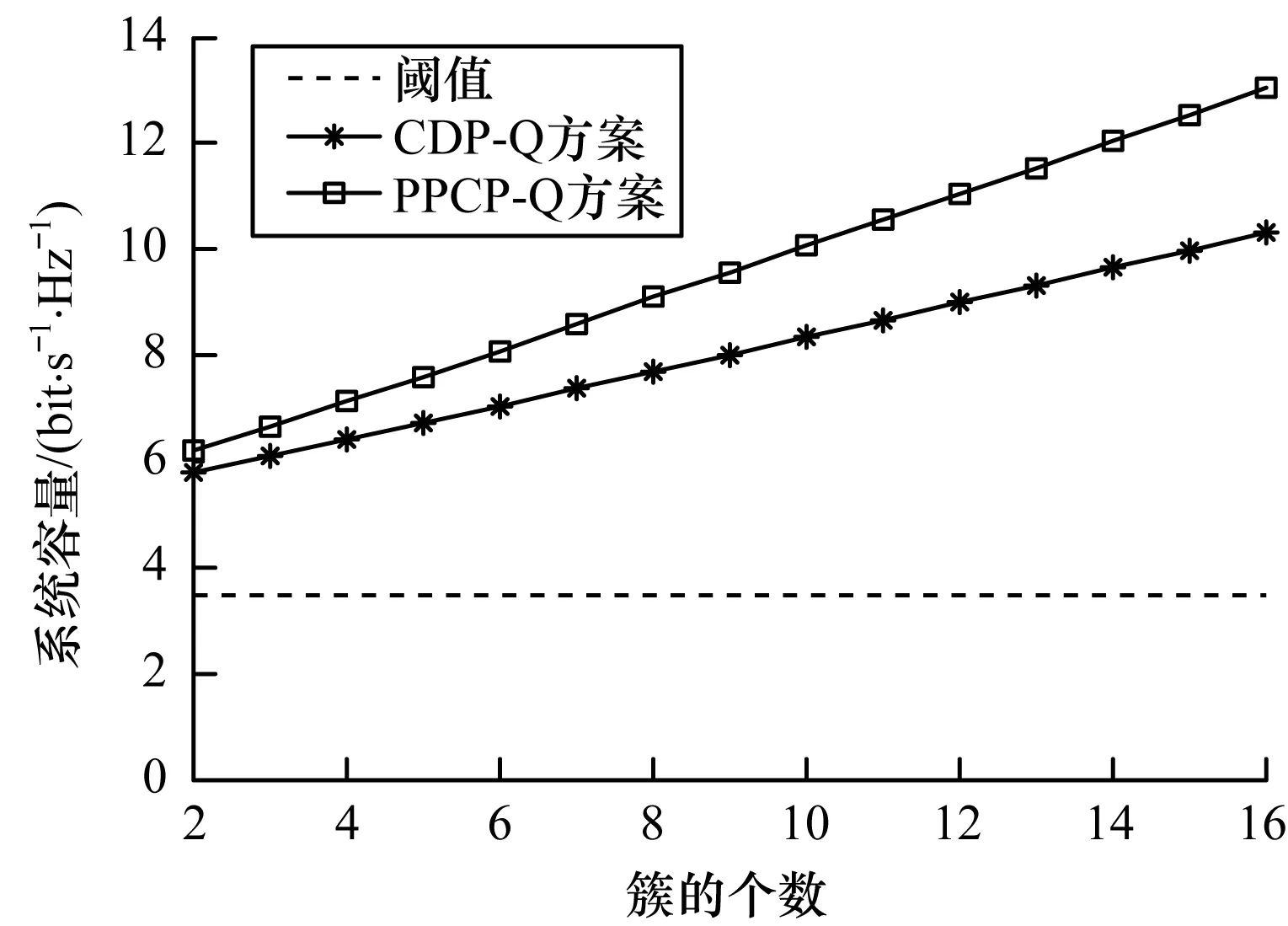
圖4 多簇情況下兩種方案的系統總容量對比Fig.4 Comparison of the total capacity of two schemesin the case of multiple clusters

圖5 兩種方案的系統容量CDF曲線對比Fig.5 Comparison of system capacity CDF curve of two schemes

5 結束語

隨著多媒體應用的不斷發展和移動流量的爆炸式增長,5G網絡中基站部署日趨密集,使毫米波通信在解決頻譜資源短缺和提升系統性能的同時也面臨高阻塞、大衰落和干擾復雜多變等問題,影響了毫米波鏈路的可用性,而且基站用戶隨機分布,無規律可循,使得功率分配問題更為復雜。對此,本文提出一種基于Q-Learning的功率分配方案。以毫米波基站為智能體,在狀態和回報函數設計中加入利己利他策略,考慮多種可能的鏈路阻塞情況,充分利用功率資源以最大化系統容量,同時保證用戶的QoS。仿真結果表明,本文方案能夠提升系統性能,實現優化目標。由于Q-Learning算法在狀態和行為設計上維度有限,因此下一步將考慮利用深度神經網絡改進該方案,并通過添加更多指標,同時實現多個系統優化目標,提升系統的整體性能。