基于隨機抽樣GMM的城市交通運行狀態模式分類

姚博凡,鄧紅平,蔡 銘

(1.中山大學 智能工程學院,廣東 深圳 518106; 2.廣東省智能交通系統重點實驗室,廣州 510006; 3.佛山交通運行監測中心,廣東 佛山 528000)

0 概述

在智能交通系統(Intelligence Transportation System, ITS)中,路段交通運行狀態模式分類始終是研究者和交通管理部門關注的重點。城市路段交通運行狀態模式分類是指按照一定的分類標準,將交通流狀態劃分為不同的等級,分別代表不同程度的暢通或擁堵情況。相比傳統的交通流特征參數(如流量、速度等),交通運行狀態更能直觀地反映當前路段的交通路況,為交通出行者提供直接的出行參考依據,幫助其制定出行路線,規避交通擁堵,從而提高出行效率,同時也可以分散交通出行量,避免交通擁堵現象進一步惡化。此外,交通運行狀態還可以為交通管理者決策提供數據支持,對于城市交通運行具有重要意義。

本文從路網路段全局適用性的角度出發,通過選取合適的聚類指標,從數據中挖掘聚類指標的分布特點,運用高斯混合模型(Gaussian Mixture Model,GMM)對路網的交通運行狀態模式進行分類,同時借助分等級抽樣聚類的方法,確定能代表路網交通運行狀態分布情況的采樣路段數,并且給出最合理的交通運行狀態分類模式數。在此基礎上,將本文方法與模糊C均值聚類(FCM)和K均值聚類(K-means)方法的分類性能進行對比,并對不同模式下的交通運行狀態加以分析。

1 相關工作

現有的交通運行狀態模式分類方法主要分為以下2類:

1)基于相關標準規范的分類方法。在國外標準方面,比較著名有美國的《道路通行能力手冊》[1],其中按照平均行程速度、密度和V/C值對交通流運行狀態進行分級評價,共分為6個等級,此外,日本、德國、澳大利亞和新西蘭也提出了相應的標準規范[2-4];在國內標準方面,有相應的國家標準《城市交通運行狀況評價規范》[5],其中以路段行程速度與自由流速度的比值作為分類指標,將交通運行狀態分為5種模式,即暢通、基本暢通、輕度擁堵、中度擁堵和嚴重擁堵,也有部分城市(如北京、上海、廣州等)提出了相應的地方標準[6-8]。

2)基于聚類的分類方法。在以往的研究中,常用的聚類方法包括模糊C均值聚類(FCM)[9-10]、K均值聚類(K-means)[11-12]和高斯混合聚類(GMM)[13-14]。前兩種方法的研究較多,而應用GMM開展交通運行狀態模式挖掘的研究相對較少。文獻[15]以流量、速度和占有率作為聚類指標,運用FCM聚類算法將交通運行狀態分為5種模式。文獻[16]在流量、速度和占有率的聚類指標基礎上,新增了流量富余度這個指標,將其定義為路段的當前流量與最大流量的差值除以最大流量。文獻[17]同樣基于FCM聚類算法,以流量、速度和占有率作為聚類指標來進行交通運行狀態聚類。文獻[18]基于K-means算法對高速路流量特征進行聚類,從而劃分交通運行狀態模式,并將結果與《道路通行能力手冊》中的分類結果進行比較。文獻[19]以交通流量、時間占有率和平均車速作為聚類指標,利用K-means聚類將交通運行狀態分為4種模式。文獻[20]選取流量和密度作為聚類指標,分車道進行K-means聚類,同時對比歐氏距離和曼哈頓距離應用于K-means聚類的不同效果,參考《道路通行能力手冊》將聚類類別數設置為6類。文獻[21]結合行程時間的高斯分布特點,利用GMM算法進行聚類,并對比聚類類別數分別設置為2和3時聚類結果的優劣性。

基于標準規范的分類方法適用性較差,因為不同地區的交通路況和交通基礎設施存在差異,對于交通運行狀態的評價標準也會有所不同。此外,不同標準規范對于分類指標的要求不一樣,部分指標很難做到全路網獲取,如流量、密度等。而基于聚類的分類方法大多以單一路段為研究對象,沒有考慮路網的整體情況。針對以上不足,本文綜合考慮城市路網中多種等級的路段,并參考《城市交通運行狀況評價規范 GB/T 33171—2016》[5],以平均行程速度和自由流速度的比值作為聚類指標,結合聚類指標自身的數據分布特點,通過GMM分等級隨機抽樣聚類算法,提出一種適用于城市路網的交通運行狀態模式分類方法。

2 數據描述與清洗

2.1 實驗數據

本文研究數據主要包含兩部分,即來自國內某導航地圖的路段速度數據和路網地圖數據。路段速度數據所在區域為佛山市路網,共計40 497條路段的377 375 568條數據記錄,數據時間范圍為2017年12月1日—2017年12月31日,時間粒度為2 min。路段速度數據的主要字段及其釋義如表1所示,其中道路等級字段共包含8種類型,分別為高速路、國道、快速路、主要道路、次要道路、省道、縣道和鄉公路。

表1 路段速度數據字段釋義Table 1 Field interpretation of road speed data

路網地圖數據為佛山市路網,共計52 752條路段,并且通過meshiid與road_id字段與路段速度數據相匹配,其主要字段及其釋義如表2所示。

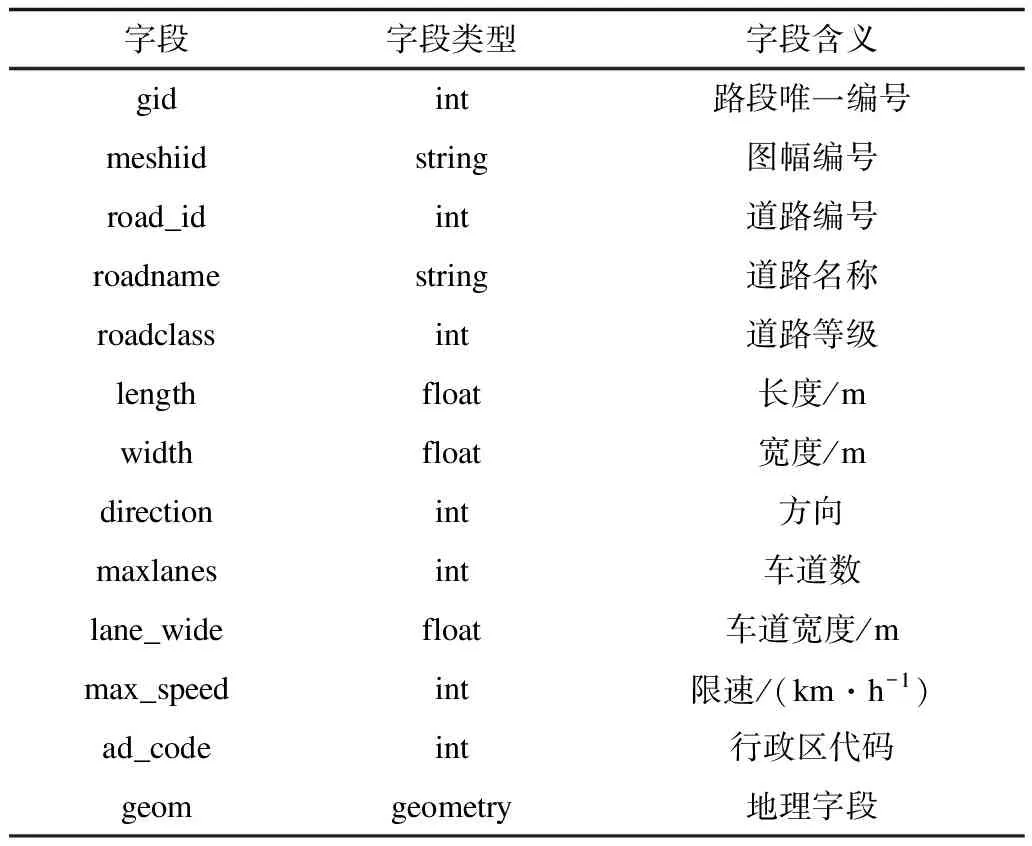
表2 路網地圖數據字段釋義Table 2 Field interpretation of road network map data

2.2 數據清洗

在路網地圖數據中,存在無數據路段、無效數據路段以及缺失數據路段,為避免對研究結果造成影響,需要對這些路段進行清除,保留有效數據路段。無數據路段指的是在數據時間跨度內沒有數據記錄的路段;無效數據路段指的是在數據時間跨度內有數據但數據的速度值多數為0的路段;缺失數據路段指的是在數據時間范圍內出現全天沒有數據的路段。這3種路段會對本文研究造成影響,因此,需要進行剔除。此外,考慮到縣道和鄉公路屬于低等級道路,很少有車輛行駛,也可能導致數據的可信度降低,因此,也需要剔除這部分路段。最終,實驗保留了高速路、國道、快速路、主要道路、次要道路和省道這6種主要城市路段,清洗后路網總路段數為34 039條,其中包含1 935條高速路路段、1 672條國道路段、952條快速路路段、14 737條主要道路路段、8 418條次要道路路段和6 325條省道路段,對應的導航地圖路段速度數據總量為317 574 210條。

3 交通運行狀態模式分類方法

3.1 高斯混合聚類原理

高斯混合聚類模型利用高斯分布概率模型來進行聚類。假設x為n維樣本空間X中的隨機向量,若其服從高斯分布,則概率密度函數可以表示為:

(1)

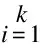
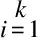
(2)

假設樣本生成過程服從高斯混合分布,首先根據先驗分布α1,α2,…,αk選擇高斯混合成分,αi為選擇第i個高斯混合成分的概率;然后根據被選擇的高斯混合成分的概率密度函數進行采樣,從而生成樣本。

若數據集D={x1,x2,…,xm}由上述高斯混合過程生成,則令隨機變量zj∈{1,2,…,k}表示生成樣本xj的高斯混合成分。顯然,zj的先驗概率P(zj=i)=αi。根據貝葉斯定理,zj的后驗分布為:

(3)

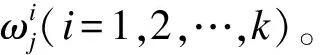
當高斯混合分布pM(x)已知時,高斯混合聚類將把樣本集D劃分為k個簇C={C1,C2,…,Ck},則每個樣本xj的簇標記κj由最大后驗概率決定,可以表示為:

(4)

對于模型的求解,關鍵在于求解參數{(αi,μi,Σi)|1≤i≤k}。根據給定樣本集D,可以采用最大化對數似然的方法,計算公式如下:

(5)

為使式(5)最大化,常用的求解方法是利用EM算法進行迭代優化,在迭代過程中不斷更新參數αi、μi和Σi。參數更新公式如下:

(6)

(7)

(8)

3.2 分等級隨機抽樣聚類

城市路網由不同道路等級的路段組成,如高速路、國道、快速路、主要道路、次要道路和省道,而不同道路等級的路段有著不同的限速,這也導致各自的自由流速度有所不同,使得不同等級路段的交通運行狀態模式分類標準有所差異。為消除這種差異,同時建立適用于全路網路段的交通運行狀態模式分類方法,本文借助歸一化的思想,利用路段的自由流速度對路段平均行程速度進行歸一化處理,并以此作為聚類指標,在高斯混合聚類的基礎上,提出分等級隨機抽樣聚類的方法。在此基礎上,分等級抽取等量的路段進行多次抽樣聚類實驗,計算前后兩次聚類結果的標準化互信息(Standardized Mutual Information,NMI)指標,通過NMI的收斂情況選擇路段抽樣數。此方法不僅可以大幅提升聚類效率,而且還能涵蓋路網各個等級路段的交通運行狀態模式。

3.2.1 聚類指標

交通運行狀態模式分類的指標有多種選擇,如流量、速度、密度等。然而,很多指標的獲取依賴于固定的交通檢測設備,如流量、密度、占有率等,這也導致這些指標無法用于大規模路網交通運行狀態模式分類。而速度的獲取則相對靈活簡單,在浮動車技術和導航地圖軟件的普及下,大規模獲得路網中路段的實時平均行程速度變得相對容易。因此,基于實驗數據,本文采用相對速度作為聚類指標,即路段平均行程速度與自由流速度的比值,這與《城市交通運行狀況評價規范 GB/T 33171—2016》[5]中的分類指標是一致的。采用該指標的好處是可以消除因道路等級差異導致的限速差異對聚類的影響,相當于對路段平均行程速度進行歸一化處理。相對速度的計算公式如下:

(9)

其中,Ri表示路段i時刻的相對速度,vi表示路段i時刻的速度,vf表示路段的自由流速度。

3.2.2 抽樣聚類流程

由于路網數據量過于龐大,如果將其全部納入聚類將會耗費大量的時間。實際上,許多路段數據的交通運行狀態模式是相似的,如果從路網中選取足夠的路段樣本,使得路段樣本的數據足以代表整個路網的交通運行狀態分布,就可以在大幅提高聚類時間效率的同時,對路網中存在的交通運行狀態模式進行挖掘分類。

基于以上思路,同時考慮到不同等級的路段,本文采用分等級隨機抽樣的思想,分別從高速路、國道、快速路、主要道路、次要道路和省道中隨機抽取n條路段,抽樣總數為6n條,以保證抽取的樣本能涵蓋6種道路等級路段的交通運行狀態模式,從而適應不同道路等級路段的分類需求。本文進行多次采樣聚類實驗,保留每次實驗的分類模型以便調用。分等級隨機抽樣聚類流程如圖1所示,目的是選取一個合適的采樣路段數,在加快聚類效率的同時,保證選取的樣本量足以代表整個路網的交通運行狀態模式分布。

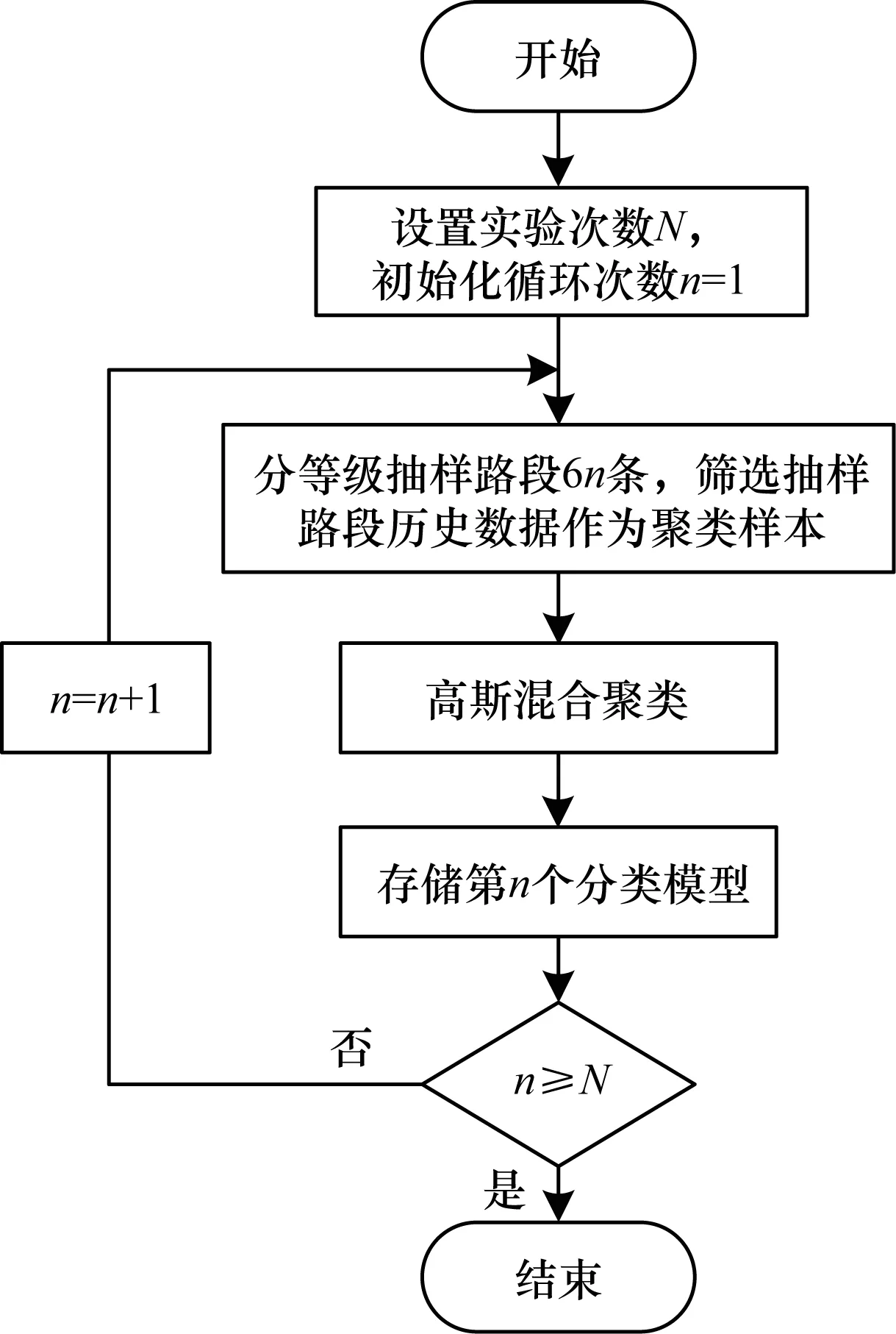
圖1 分等級隨機抽樣聚類流程Fig.1 Procedure of hierarchical random sampling clustering

分等級隨機抽樣聚類步驟如下:

步驟1設置實驗次數N,初始化循環次數n=1。

步驟2分別從6類道路等級路段中抽取n條路段,從歷史數據集中篩選相應的6n條路段的數據。

步驟3對抽樣的路段數據進行高斯混合聚類。

步驟4存儲計算完畢的分類模型。

步驟5判斷是否達到實驗次數,達到則退出循環,否則n遞增1,重復步驟2～步驟4。

3.2.3 采樣路段數確定流程

采樣路段數確定流程如圖2所示。通過隨機選取1 000條路段的數據作為驗證集,對上文中得到的n個聚類模型進行驗證,得到對應的n種交通運行狀態分類結果,按聚類樣本量從小到大的順序計算前后2種分類結果的NMI指標,得到(n-1)個NMI值。隨著聚類樣本量的增加,當NMI基本保持不變時,可以認為隨著聚類樣本量的增加,模式分類結果基本不變。可以將此過程看作是一個近似收斂的過程,說明此時采樣路段具有代表性,采樣路段的交通運行狀態模式分布足以代表整個路網的交通運行狀態模式分布。

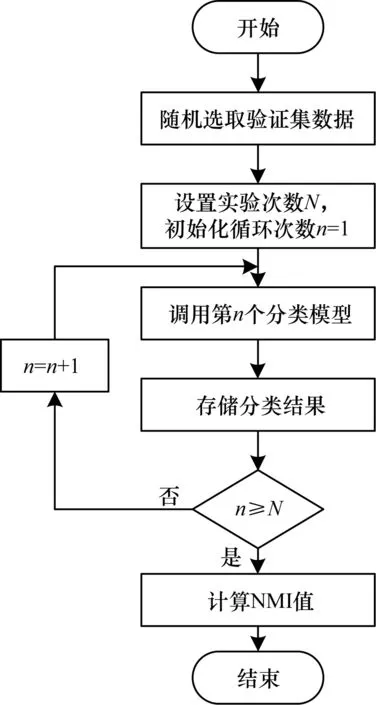
圖2 采樣路段數確定流程Fig.2 Procedure of determining the number of sampled roads

采樣路段數確定步驟如下:

步驟1隨機選取1 000條路段數據形成驗證集數據。

步驟2設置實驗次數N,初始化循環次數n=1。

步驟3調用第n個分類模型,計算分類結果。

步驟4存儲第n個分類模型的分類結果。

步驟5判斷是否達到實驗次數,達到則退出循環,否則n遞增1,重復步驟3和步驟4。

步驟6計算NMI值。

NMI是聚類中常用來衡量兩個聚類結果相似度的指標,取值范圍為[0,1],越接近1代表兩次聚類結果越接近。實驗對前后兩次聚類的模式分類結果計算NMI值,如果前后兩次聚類的NMI非常接近1且基本保持不變,說明采樣路段數已達到合適的值。

4 實驗與結果分析

4.1 分等級隨機抽樣聚類結果

實驗中聚類的歷史數據時間為2017年12月1日—2017年12月24日,將聚類模式數設置為5,關于聚類模式數的選取依據將在下文進行說明。聚類實驗循環進行850次,得到對應的850個聚類模型。通過圖2流程確定采樣路段數,驗證集的數據時間為2017年12月25日—2017年12月31日,繪制NMI變化曲線,如圖3所示。從中可以看出,當采樣路段數大于3 000時,曲線大致收斂在0.95以上,說明此時的交通運行狀態模式分類結果的差異較小。因此,確定采樣路段數為3 600條,因為即使再增加采樣數,不僅對分類結果的影響很小,而且聚類時間也會增加,說明此時的采樣數是較為合理的。

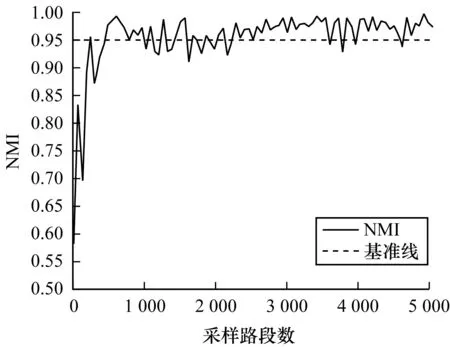
圖3 NMI隨采樣路段數的變化曲線Fig.3 Changing curve of NMI with number of sampled roads

4.2 相對速度分布模式

為探究數據自身的模式分布特點,對相對速度的分布進行分析,計算其分布頻率。相對速度是一系列離散值,范圍為[0,1],為進行頻率統計,將[0,1]劃分為100個小區間,區間長度為0.01,統計每個區間內的樣本數,采樣路段數為3 600條。計算其在2017年12月1日—2017年12月24日期間的相對速度分布頻率,并利用高斯分布函數進行擬合,從而得到相對速度的分布頻率直方圖和密度曲線,如圖4所示。從中可以看出,基于相對速度指標可以將交通運行狀態模式分為5類,并且每一類均大致服從高斯分布,這也是本文采取GMM聚類模型對數據樣本進行模式分類的原因。

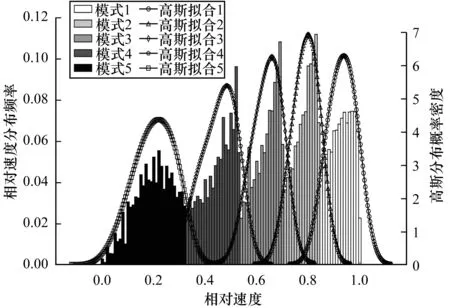
圖4 相對速度分布模式Fig.4 Distribution mode of relative speed

4.3 不同聚類模式數比較

現有的研究和相關標準通常將交通運行狀態模式分為3類～6類不等,進而分別描述不同程度的暢通和擁堵狀態模式。為使得模式數的確定有客觀依據,本文比較不同模式數下的聚類結果。實驗中將模式數a設為2～9,對于每一組單獨進行聚類實驗,每一組聚類結果對應的各個模式的聚類中心相對速度如表3所示。從中可以看出,當模式數大于5時,部分模式的聚類中心出現了明顯的重疊,即交通運行狀態模式無法被明顯區分,顯然此時的模式數設置過大,數據中的交通運行狀態模式數應小于等于5。

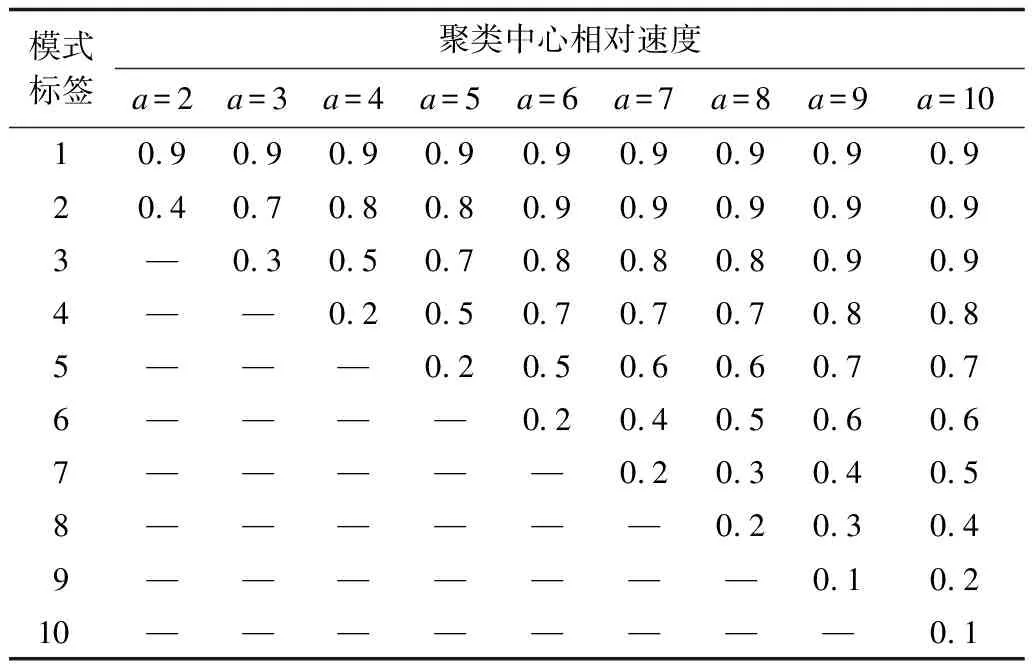
表3 不同聚類模式數下的聚類中心相對速度Table 3 Relative speeds of cluster centers underdifferent numbers of clustering mode

由表3可以看出,當模式數大于5時,交通運行狀模式已經出現重疊,因此,不考慮模式數大于5的情況。為進一步比較模式數為2～5的聚類結果,本文計算DBI指標。DBI是聚類中常用來評價聚類效果優劣的指標,其值越小,表明類內距離越小,類間距離越大,聚類效果越好。由圖5可以看出,隨著聚類模式數的增加,DBI逐漸減小,當模式數為5時,DBI最小,表明此時聚類效果最優。因此,本文將聚類模式數確定為5。

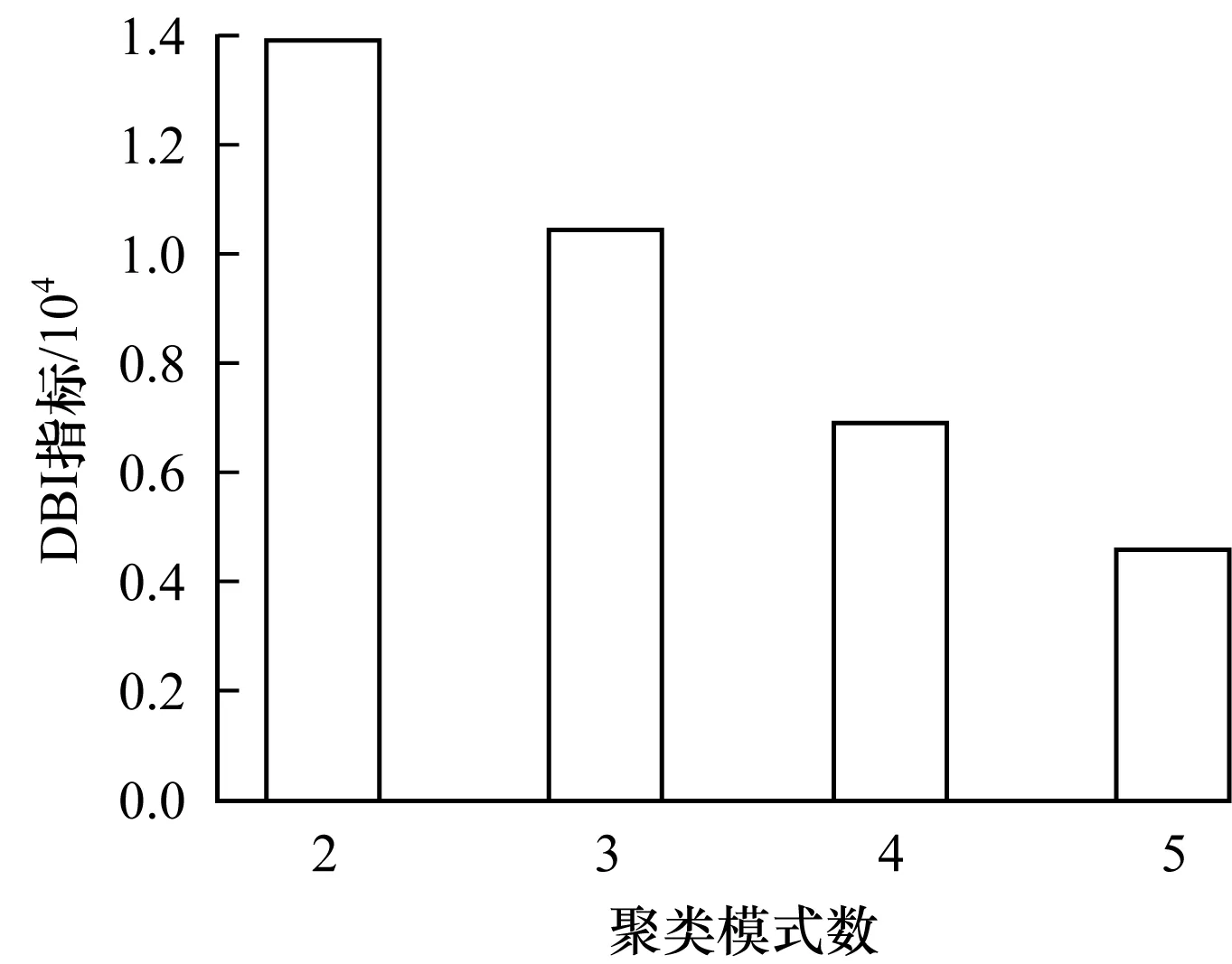
圖5 DBI指標隨聚類模式數的變化曲線Fig.5 Changing curve of DBI index with number ofclustering modes

4.4 不同方法比較

將本文GMM聚類結果與國標(GB/T 33171—2016)、FCM聚類和K-means聚類的結果進行相關性分析,分析相對速度與模式分類標簽的相關性,并計算不同方法分類結果的DBI指標,從而對比不同分類方法的優劣性。首先可以確定的是,相對速度與模式分類標簽是呈現負相關的,因為實驗中模式標簽越大,平均相對速度越小。由表4可以看出,GMM聚類的負相關性最強,DBI雖然比FCM和K-means聚類的略大,但是由于聚類樣本量是千萬級的,因此DBI的差異分攤到每個樣本上幾乎為0,對結果的影響可忽略。綜合對比來看,GMM聚類對于相對速度分布的可解釋性更好,而且相關性比其他方法更強。此外,國標分類結果的相關系數表現不佳,說明了國標不能適應各地的交通路況實情。

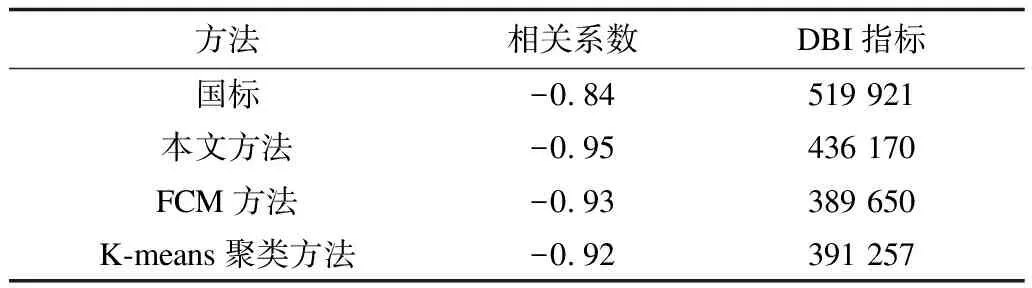
表4 不同方法的相關系數與DBI指標Table 4 Correlation coefficients and DBI indexes ofdifferent methods

4.5 不同模式下交通運行狀態分析

本文對不同模式下的整體交通運行狀態進行分析,并且對其時間分布頻率進行統計,結果如圖6所示。由表3可知:在模式數為5的情況下,模式1～模式5的聚類中心點相對速度逐漸減小,表明交通運行狀態在逐漸變差;模式1與模式2的相對速度較大,表明這兩類模式的交通運行狀態比較接近自由流下的交通運行狀態,屬于暢通的狀態。從圖6中也可以看出:這兩類模式在時間分布上比較均勻,沒有出現明顯的峰值;而從模式3開始,相對速度明顯變小,特別是模式4和模式5,并且它們在時間分布上呈現出明顯的雙峰現象,集中在早晚高峰,此時是交通出行高峰期,最大的特點就是會出現交通擁堵,說明這三類模式是屬于擁堵狀態;模式3是從暢通到出現擁堵的過渡狀態,雙峰分布初步顯現;模式4和模式5的雙峰分布則十分顯著,并且模式4的擁堵程度高于模式3,模式5的擁堵程度高于模式4。

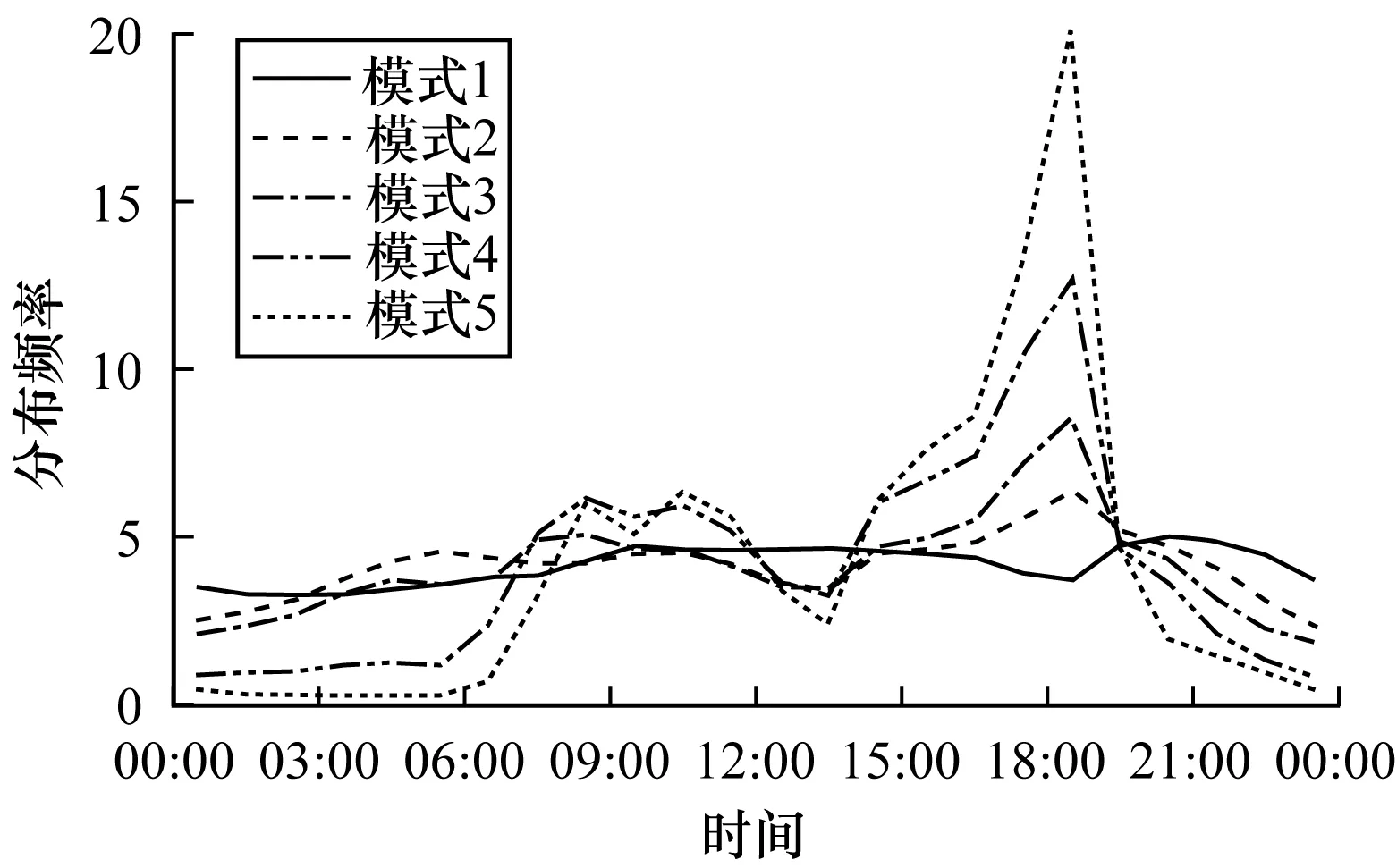
圖6 不同模式的時間分布Fig.6 Temporal distribution of different modes

5 結束語

針對現有城市路段交通運行狀態模式分類研究適用性差和研究對象單一等不足,本文提出一種基于高斯混合分等級隨機抽樣聚類的交通運行狀態模式分類方法。以佛山市為例,利用導航地圖的路段速度數據,在參考國標分類指標的基礎上以相對速度為聚類指標分析相對速度模式分布,發現交通運行狀態模式存在類似高斯混合分布的特點,因此采用高斯混合聚類的方法。面對大樣本量聚類,進一步提出基于分等級隨機抽樣的聚類方式以提高聚類時間效率。實驗結果表明,GMM聚類具有較好的可解釋性,同時能合理劃分交通運行狀態模式。本文方法結合分等級隨機抽樣的思想和數據自身特點,通過高斯混合聚類實現了大規模數據下城市路段交通運行狀態模式的有效挖掘,具有較好的可解釋性和適用性。下一步將在本文研究基礎上采用深度學習方法對交通運行狀態進行預測,并基于交通運行狀態模式分類探究路網交通運行狀態的演變趨勢。