高中數學函數與方程綜合問題探究

◇ 安徽 應 莉

(作者單位:安徽省阜南一中)

函數與方程是高中數學的重要知識點,尤其是一些題型常將兩者結合起來,難度較大.為提高學生解答該類問題的能力,教學中應注重做好相關習題的匯總,與學生一起探究解題思路,使其遇到類似問題時能快速解答.

1 運用圖形,簡化解題

可將有關函數零點的問題轉化為方程問題,運用數形結合法求解,大大簡化解題步驟,提高解題效率.教學中注重優選、講解經典例題,使學生掌握運用數形結合法解答函數與方程綜合問題的具體步驟.同時,鼓勵學生進行課堂反思,把握解題的關鍵,在解題中少走彎路,盡快得出正確結果.

例1已知函數g(x)＝f(x)＋x＋a,若g(x)存在2個零點,則a 的取值范圍為( ).

A.[－1,0) B.[0,＋∞)

C.[－1,＋∞) D.[1,＋∞)

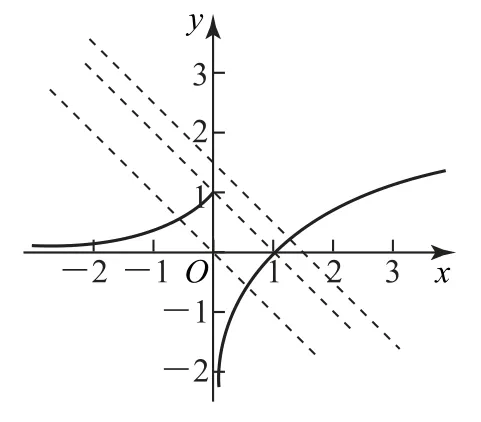
圖1

這是一道高考題,求解時,可對已知條件進行轉化,再應用數形結合思想進行分析.g(x)存在2個零點等價于f(x)＝－x－a 存在2 個不等實根.在同一直角坐標系中分別繪制f(x)和y＝－x－a 的圖象,如圖1,因為y＝－x－a圖象的斜率為－1,而－a 表示在y 軸上的截距,因此,要想滿足題意,只需－a≤1,即a≥－1,故選C.

2 深挖條件,巧妙突破

解答函數與方程的綜合問題時需認真審題,充分挖掘題干中的隱含條件,實現快速破題.教學中可結合學生的所學知識,注重在知識的交會處設計問題,并給學生專門留下獨立思考的時間,鼓勵其積極回顧所學知識,深挖已知條件進行問題求解,在鞏固所學知識的同時,使其更好地掌握函數與方程綜合問題的解題技巧.

例2若a,b 為函數f(x)＝x2－px＋q (p＞0,q＞0)的2個不同零點,且a,b,－2這3個數可適當排序后成等差數列,也可適當排序后成等比數列,則p＋q 的值為( ).

A.6 B.7 C.8 D.9

解答該題需要充分理解零點的含義,并根據數列知識求出p＋q 的值.很多學生面對該題時,會因無法巧妙應用題干中“等比數列”“等差數列”的相關知識,而無從下手.事實上,因為a,b 為方程x2－px＋q＝0的兩個不等實根,由根與系數間的關系得a＋b＝p,ab＝q,又因為p＞0,q＞0,則a＞0,b＞0.若a,b,－2排序后為等比數列,則－2必為第二項,該等比數列為a,－2,b 或者b,－2,a,因此,必有ab＝4;若a,b,－2適當排序后為等差數列,則a－2＝2b 或b－2＝2a,解得a＝4,b＝1或a＝1,b＝4,則p＝5,q＝4,則p＋q 的值為9,故選D.

3 等價轉化,巧用性質

解答高中數學函數與方程綜合問題時應注重運用等價轉化思想、巧用函數的相關性質.教學中為使學生掌握等價轉化的方法,教師應注重選擇代表性較強的習題,組織學生開展訓練活動,使學生在訓練中發現并彌補知識的漏洞,積累相關的解題經驗.

例3已知方程x＝a(a 為常數)在區間[0,2π]上恰有三個根x1,x2,x3,則x1＋x2＋x3的值為( ).

方程中涉及三角函數,一般情況下根無法直接求解.解題時可將其轉化為函數問題,借助函數圖象分析.因為令根據三角函數性質易得函數f(x)在上單調遞增,在上單調遞減,要想滿足題意則需得出x＝1故選C.

總之,高中數學教學中為提高學生解答函數與方程綜合問題的能力,促進學生數學成績的提升,教師應注重講解例題,積極組織學生開展專題訓練活動,使學生掌握相關的解題技巧.