數學形象思維能力的培養策略

林翠英

摘? 要：從思維的抽象性角度來看，思維可以分為直觀行為思維、具體形象思維和抽象邏輯思維三種。不少教師在發展學生的抽象邏輯思維能力上花費了不少精力，但效果甚微。究其主要原因還在于前期沒有形成良好的具體形象思維能力。文章就如何培養學生的數學形象思維能力展開分析。

關鍵詞：形象思維;表象;直感;想象

思維指人體接受、儲存、加工以及輸出信息的過程，是人腦對客觀事物的內部規律或本質屬性的反映。隨著教育改革的推進，發展學生的抽象邏輯思維是很多一線教師不斷努力的方向，而忽略了培養學生的形象思維是獲得抽象邏輯思維能力的基礎，更符合小學生的認知規律。因此，我們教師應從思想和行動上重視形象思維能力的培養，這是發展學生思維能力本身的需求，也是提高課堂效率，發展學生數學思維的需要。

一、豐富表象，夯實基礎

所謂的“表象”是以往感知過的客觀事物在人腦再次出現，是形象思維形成的基礎。心理學家研究發現視覺系統是人類獲取信息的主要途徑，要豐富表象的累積，可提供如掛圖、實物、模型等物品，讓學生通過觀察獲取表象信息 [1]。感知是數學表象的根本，豐富的感知能形成高概括性的表象。這需要教師引導學生通過多形式、多方位、多系統地參與、觀察或操作數學現象，構建豐富的數學表象，夯實思維發展的基礎。

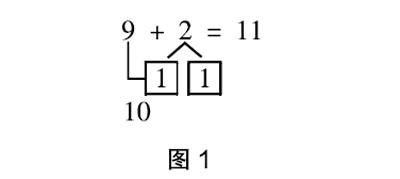
例1：“9+幾”的教學。

問題：框內有9只球，框外有2只球，一共有多少只球？

教師根據這道題，提前準備道具引導學生動手操作把框外的一只球放到框內，此時框內有10只球，框外有1只球，合計11只球，這是最原始階段的直觀行為思維。若想進一步建立具體的形象思維，教師可引導學生思考：9只球加上2只球，一共是11只球。換成算式應該怎樣計算呢？這里是把兩只球怎么分的，分別與誰搭檔而得出結論？學生經思考后得出以下分解式（見圖1），這是直觀行為思維向具體形象思維轉變的過程，也是小學低年級數學課堂教學常用的方法，這種方法借助外化了的圖式表象，能舉一反三地推導出20以內的進位加法法則。

由此可見，數學課堂教學過程中進行直觀演示操作后，學生雖然能解決題干中的問題，但思維發展僅局限于直觀階段。若通過圖式表象去揭示問題的內涵，學生就能理解問題的本質并產生解決同一類問題的能力。因此，教師可通過圖式表象的方法，引導學生從直觀思維轉變到具體形象思維，逐漸形成空間概念。

二、關注直感，增加數學想象

所謂的“直感”是指人體對具體事物的感受。數學直感可歸納為模式補形直感、形象識別直感、象質轉換直感和形象相似直感四類，小學生以形象識別直感和模式補形直感為主，他們判斷一個數學形象時不必以語言和概念為中介，只需調動大腦中原有的一般表象與對應物進行對比即可。

1. 形象識別直感的訓練

所謂的“形象識別直感”是指用數學基礎表象的類象與具體對象的個別現象進行比較，再根據兩者特征的相似性來判斷個象與類象是不是同質的思維方式。學生這種直感能力體現在對各類圖式、圖形的變式的再認。因此，教師在課堂教學中應關注學生的形象識別直感，通過反復多次訓練學生的變式、變圖能力，以提高他們的數學想象力。

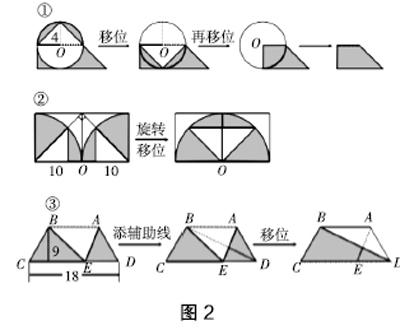
例2：求下列圖形（見圖2）陰影部分的面積。（單位：米）

此題需學生從復雜的圖里識別到與一般圖形同質的形象特征，將復雜的圖形通過旋轉、移位或添加輔助線等方式分解出學生所熟悉的基本圖形，圖形在大腦中運動變化成基本圖形后，學生快速識別且計算出陰影部分的面積。這種方法需建立在學生對基本圖形熟識的基礎上，多次訓練可增加形象識別直感的熟練度。

2. 模式補形直感的訓練

所謂的“模式補形直感”是運用大腦已形成的表象模式對圖形部分特征一樣的內容進行表象補形、整合的思維形式。根據小學生的思維特征，常將補形法的思維機制運用于解決問題，以增強學習者的想象力。

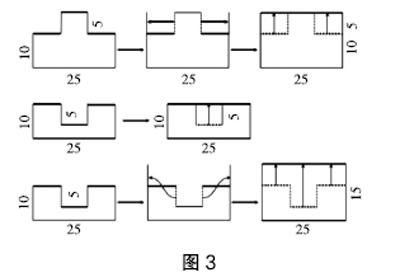
例3：求下列圖形（見圖3）的周長。（單位：米）

這組圖形周長的計算，同樣需要教師引導學生從不規則的圖形里尋找出與基本圖形的同質特征，通過移動不規則圖形的線段，將殘缺不規整的圖形補充成規整的學生所熟悉的圖形，便于學生快速識別并計算出圖形的周長。這是典型的使用模式補形直感的方式解決數學問題，學生在線段的等價變換中將復雜的問題簡單化，熟練掌握這種方法能幫助學生形成豐富的表象模式，更好地解決更多的數學問題。

三、發揮想象，突破自我

愛因斯坦曾經說過：“比知識更重要的是想象力，它是知識進化的源泉，是科學研究的重要因素。”想象作為一種特殊的思維形式，是大腦突破時空束縛，將原儲存的表象進行加工和改造產生新表象的過程 [2]。表象是想象的原材料，直感是想象的基本手段，當表象與直感在人腦中有機聯合就形成新的形象。數學想象是學生創造性思維形成的必需品，離開想象就失去了創造的靈感。從其內容形式角度來看，有圖形和圖式兩類想象;從它的獨立性角度和新穎性來看，有創造性和再創造性兩類想象 [3]。發展小學生的想象能力，可理論聯系實際從生活實中尋找合適的素材，引導學生將理論的數學和實際的生活聯系在一起思考問題。

例4：“圓的認識”，在各種場景下畫圓。

師：同學們都已經學會了怎樣用圓規在本子上畫圓，現在老師想在黑板上畫一個圓，沒有帶大圓規怎么辦呢？

生：把呼啦圈扣在黑板上，用粉筆沿邊畫一圈。

師：這方法好，如果我們想在教室里畫個中心圓，你們有什么辦法嗎？

生：我看到過體育老師畫投擲實心球的圈，人站在中間為圓心，手上持裝有白灰的大勺子，保持手臂姿勢的固定，人邊旋轉邊讓勺子里的白灰灑在地上，當一圈兒轉完，圓就畫成了。

師：這位同學觀察得非常仔細，值得表揚。如果我們想要挖一個圓形的魚池，有什么辦法畫圓呢？

生：取一根足夠長的繩子，固定一端，另一端繞地一圈兒，就能獲得圓形的魚池了。

師：這個方法不錯，如果要在我們這個區建造一條圓形的環城高架，大家覺得有什么辦法畫這個大圓呢？（教室瞬間安靜下來）

生（底氣不足地說）：在中心點放置一臺信號發射機，給在圓邊上的坦克發送信號，塔克沿著信號開一圈。

師：想法不錯，問題是遇到房屋等阻礙物怎么辦呢？

生：用飛機，邊開邊撒白石灰。

（其他學生七嘴八舌地表示這個方法不可行，石灰會污染環境還會被風吹得到處都是，不能畫成圓）

師：想想我們的設計師是怎樣做到的呢？

生：我知道了，只要在區域地圖上畫一個圓就行了，在圓邊上的建筑物可以拆遷，遇到河流可以修橋。

（話音剛落，掌聲就響起來了）

這是一個引導學生根據生活展開想象的真實案例，教師引導學生從畫小圓開始，逐漸放大圓的面積，直至無法人為地去畫為止。學生在此過程中不斷突破原有的空間束縛，對畫圓的方法不斷進行加工改造，直至新的方法產生，這也是學生通過想象挑戰自我，突破自我的表現。

綜上所述，發展小學生的數學思維能力首先要培養他們的形象思維，教師可挖掘教材和生活中的素材，從直觀、表象和想象三個方面有意識地引導學生，將培養學生的數學形象思維滲透到課堂教學的各個環節，為促使學生形成更高級的抽象邏輯思維夯實基礎。

參考文獻：

[1]? 任樟輝. 數學思維論[M]. 南寧：廣西教育出版社，1996.

[2]? 郭思樂. 數學思維教育論[M]. 上海：上海教育出版社，1997.

[3]? 吳球. 小學數學教學中對學生邏輯思維能力的培養探究[J]. 學周刊，2012（23）.