解綜合性三角函數問題的技巧與方法
◇ 江蘇 顧建華
眾所周知,解三角函數問題是高考的一個重要內容,在選擇題、填空題以及解答題中均有涉及,難度適中,這樣的題目一般是不能丟分的.因此,掌握好解題方法非常關鍵.本文主要介紹高考數學中的解三角函數問題的方法技巧.
1 了解一些三角函數重要的關系
1)同角三角函數的基本關系
a)平方關系:sin2α+cos2α=1;
c)倒數關系:tanαcotα=1.
2)誘導公式
a)設α為任意角,k∈Z,
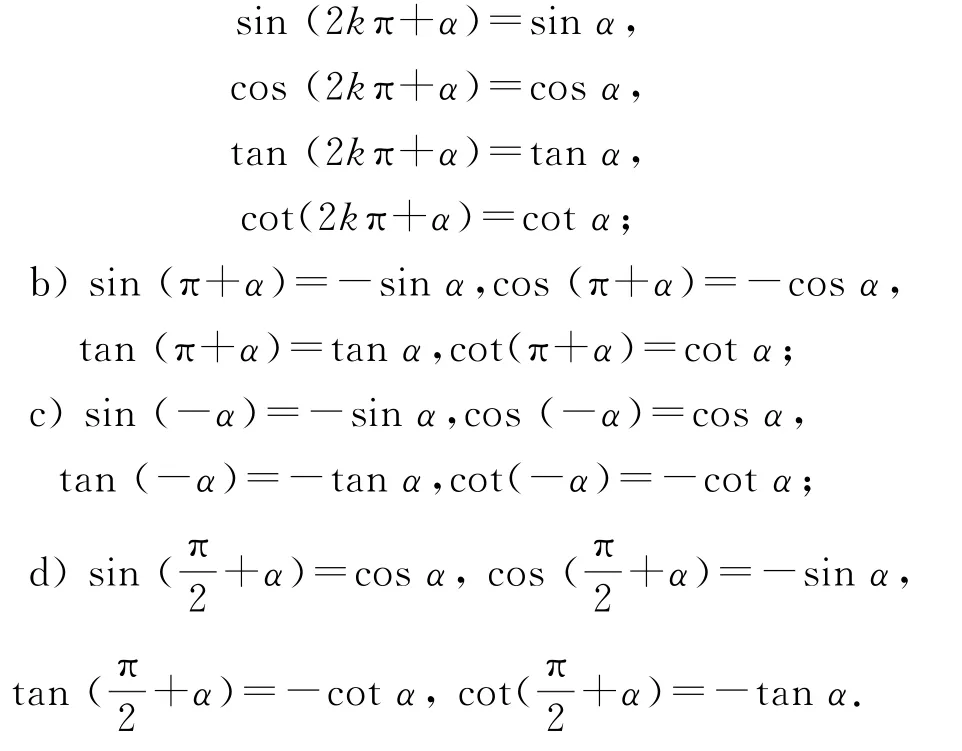
3)和差公式
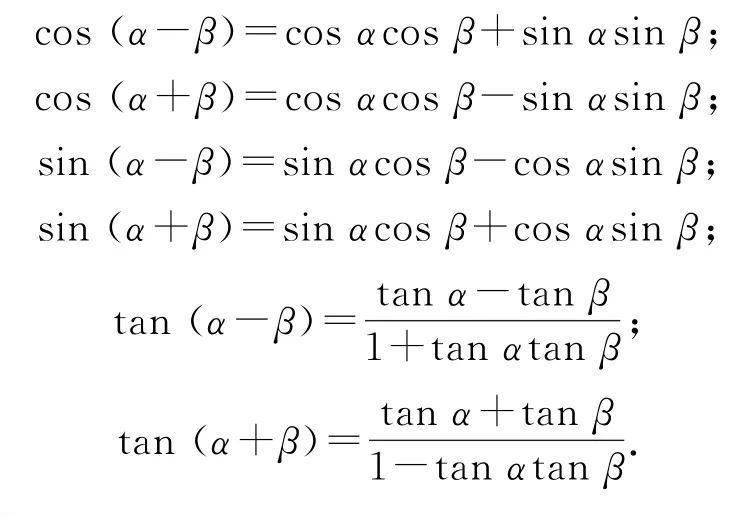
注:公式的逆用或者變形.
4)二倍角的正弦、余弦和正切公式
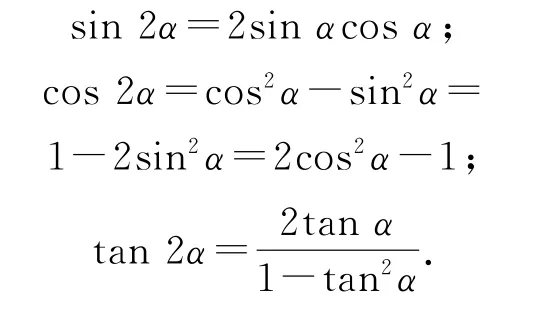
從二倍角的余弦公式里面可以得出降冪公式,即
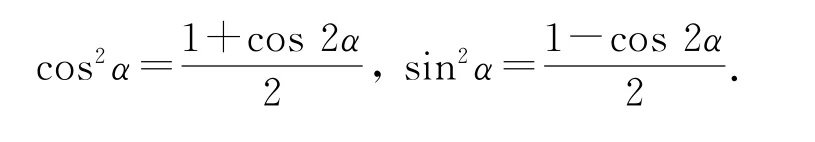
5)輔助角公式
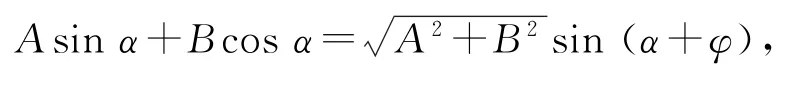
6)半角公式(可由降冪公式推導出)
金融工具的有效性與金融服務的完善必須依托國家的政策為導向,創新投融資平臺,建立全體系與全產業的金融服務機制,通過重點項目拓寬現有的投融資渠道,準確發揮金融在貴陽城鎮化建設過程中的積極作用。
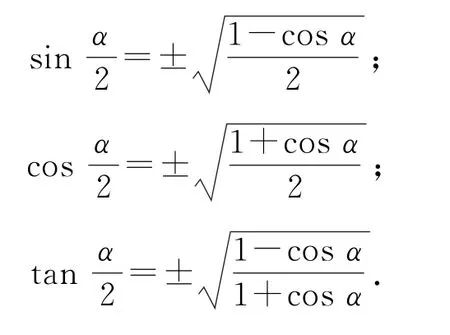
2 例題分析
例1已知tanα=3,求的值.
解析
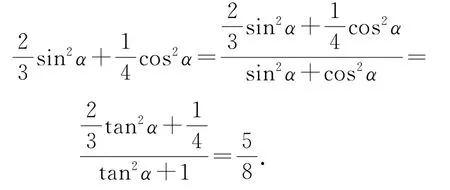
點評
利用同角三角函數的基本關系靈活轉化,把未知變成與已知條件有關,找到突破點.
例2已知求sinαcosα的值.
解析
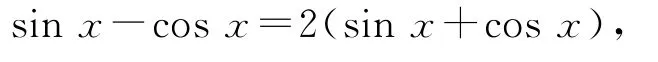
化簡可得sinx=-3cos x.又因為sin2α+cos2α=1,可聯立方程組
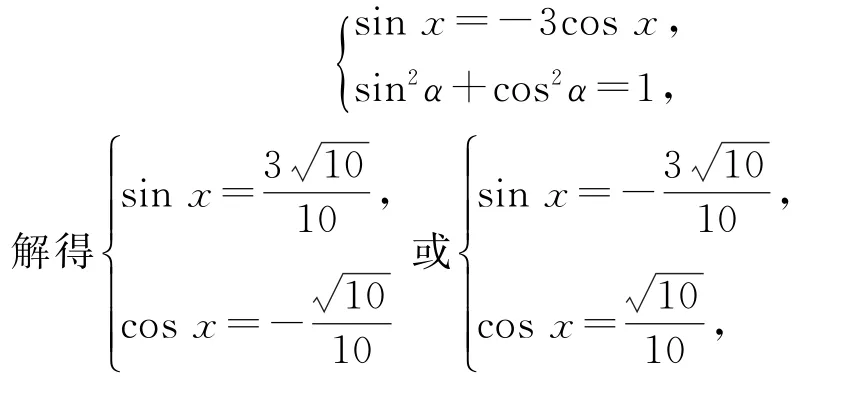
方法2因為所以
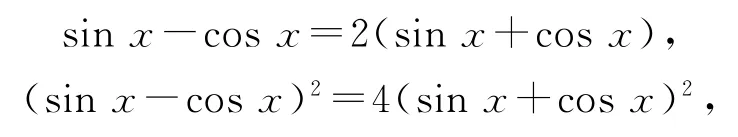
則1-2sinαcosα=4+8sinαcosα,所以有
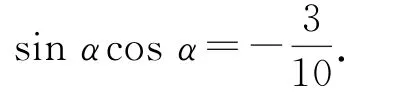
點評
三角函數恒等變形的基本策略有常值代換特別是用“1”代換,如sin2α+cos2α=1)、項的分拆與角的配湊、降次與升次、化弦法、引用輔助角公式等.
例3在△ABC中
(1)求sinA的值;
(2)設△ABC的面積求BC的長.
解析

(2)由三角形面積計算公式,得
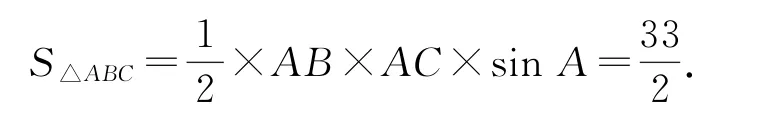
點評
解答高考題中三角函數應用題的策略:首先,觀察角以及運算關系間的差異;其次,運用相關公式,找出差異之間的內在聯系;最后,選擇恰當的公式,促成差異的轉化.
三角恒等變形,是三角知識的綜合應用,雖然題目類型多樣,變化復雜,但處理這類問題其實很簡單,我們只需要把三角函數的項數盡可能變少,類型盡可能減少,角盡可能變小,次數盡可能變低,分母盡可能不含三角式、不帶根號,能求出值的求出值.然后,我們要注意不同角之間的關系,盡量異名化同名,異角化同角.

