小議“構造函數”巧解不等式

◇ 山東 李百玲

提升學生高中數學能力,除了掌握必要的基礎知識,更重要的是學生對數學思想方法的靈活運用.函數與方程、轉化與化歸是高中數學中比較重要的兩大思想,而構造函數的解題思路恰好是這兩種思想的良好體現.

在近幾年高考數學試卷中,許多與函數相關的解不等式的題目,尤其是壓軸小題,經常能用到構造函數法.所謂構造函數是指通過一定方式,設計并構造一個與待解答問題相關的函數,并探究其單調性,借助圖象或利用運算結果,從而得到不等式的解集.本文重點探討如何合理地構造函數.

1 構造f(x)與x的關系

當題目所給的不等式中除了f(x)外,僅含有x,常用的構造形式有.對于xf′(x)＋f(x)＞0,構造h(x)＝x f(x);對于x f′(x)－f(x)＞0,構造.

例1設f(x)是定義在R上的偶函數,當x＜0時,f(x)＋x f′(x)＜0,且f(－4)＝0,則不等式xf(x)＞0的解集為________.

解析

設F(x)＝x f(x),則有F′(x)＝f(x)＋xf′(x),當x＜0時,f(x)＋xf′(x)＜0,F′(x)＜0,所以F(x)在(－∞,0)上單調遞減.因為f(x)為偶函數,x為奇函數,所以F(x)為奇函數,故F(x)在(0,＋∞)上也單調遞減.

根據f(－4)＝0可得F(－4)＝0,從而函數圖象如圖1所示,根據圖象知x f(x)＞0的解集為(－∞,－4)∪(0,4).

圖1

變式f(x)是定義在R上的偶函數,且f(1)＝0,當x＜0時,有xf′(x)－f(x)＞0恒成立,則不等式f(x)＞0的解集為________.

解析

2 構造f(x)與e x的關系

由于(ex)′＝ex,當給出的不等式中出現f(x)±f′(x)型,我們首先考慮f(x)與ex的關系,和的形式優先考慮構造F(x)＝f(x)·ex,差的形式優先考慮構造.

例2已知f(x)是定義在R上的函數,導函數f′(x)滿足f′(x)＜f(x)對于x∈R恒成立,則有( ).

A.f(2)＞e2f(0),f(2 020)＞e2020f(0)

B.f(2)＜e2f(0),f(2 020)＞e2020f(0)

C.f(2)＞e2f(0),f(2 020)＜e2020f(0)

D.f(2)＜e2f(0),f(2 020)＜e2020f(0)

解析

變式已知定義在R上的偶函數f(x)的導函數為f′(x),滿足f(0)＝e2且f(x)＞f′(－x),則關于x的不等式的解集為( ).

A.(－∞,－2) B.(－2,＋∞)

C.(－∞,0) D.(0,＋∞)

解析

根據原函數是偶函數可知f′(－x)為奇函數,又f′(－x)－f(x)＜0,故構造函數F(x)＝f(x)ex,其在R上單調遞增,將f(x＋2)＞轉化為F(x＋2)＞F(0),再根據其單調性可得x＋2＞0,從而B選項正確.

3 構造f(x)與sin x,cos x的關系

類比前兩類,若題中出現三角函數,就需要構造f(x)與sinx,cosx結合的函數,具體如下:

例3已知函數y＝f(x)對于任意滿足f′(x)cosx＋f(x)sinx＞0(其中f′(x)是f(x)的導函數),則下列不等式不成立的是( ).

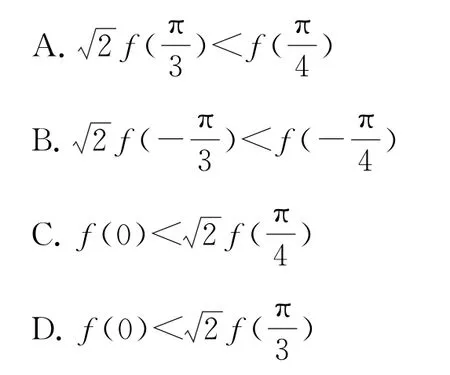
解析

變式已知且αsinα－βsinβ＞0,則下列結論正確的是( ).

A.α＞βB.α2＞β2

C.α＜βD.α＋β＞0

解析

構造f(x)＝xsinx,則f′(x)＝sinx＋時,導函數f′(x)≥0,f(x)單調遞增時,f′(x)＜0,f(x)單調遞減.又因為f(x)為偶函數,根據單調性可知選B.

以上是構造函數在解決與不等式有關的小題中的應用,在求解時,根據問題的條件或目標,構造出一種新的函數關系,在新函數下轉化并利用函數的有關性質解決原問題,這是一種行之有效的解題手段.構造函數法解題具有較大的靈活性和技巧性.根據要解決的問題,靈活構造轉化,有的放矢,從而使問題迎刃而解.