縱向聯(lián)盟視角下港航企業(yè)間的船期協(xié)調優(yōu)化

尹長永，杜沂霖

（大連海事大學 交通運輸工程學院，遼寧 大連 116000）

1 引言

當前，在全球經濟一體化不斷深化的現(xiàn)實背景下，為了求生存共發(fā)展，港航聯(lián)盟已經成為全球航運業(yè)的重要發(fā)展方向之一。港、航企業(yè)通過不同的分工協(xié)作，實現(xiàn)了客戶在供應鏈上物資的有效流動，并為此獲取相應的增值收益。貨運需求量是影響港航收益的主要源泉，船期安排直接關乎港航雙方的經濟效益。合理安排船期計劃有利于共同發(fā)展，增加港、航企業(yè)的收益。因此，在競爭日益激烈的市場環(huán)境下，研究港航雙方船期計劃的協(xié)調問題有著重要的現(xiàn)實意義。

關于縱向聯(lián)盟的研究，管理學家邁克爾·波特[1]將戰(zhàn)略聯(lián)盟劃分為橫向聯(lián)盟和縱向聯(lián)盟這兩種類型，其依據主要是在價值鏈中聯(lián)盟主體是否處于相同的環(huán)節(jié)。Foros等[2]研究了電信市場中的縱向分離戰(zhàn)略，探討了上游公司如何通過使用價格相關的利潤分享規(guī)則來防止產生具有替代性產品的下游公司之間的破壞性競爭。Matsushima等[3]則通過以多種原材料供應為背景，表明縱向聯(lián)盟能夠有效降低企業(yè)的交易成本，從而增加整個系統(tǒng)的總利潤。關于縱向聯(lián)盟方面的研究，大多停留在基礎理論上，在實踐方面仍未得到較廣泛的應用。

關于港航聯(lián)盟的產生，聯(lián)合國貿易與發(fā)展會議（UNCTAD 1999）[4]提出了第四代港口主要是縱向和橫向一體化戰(zhàn)略的觀點。董玉桂[5]研究了變化莫測的航運市場對港口物流業(yè)的影響，并重點分析了縱向聯(lián)盟和橫向聯(lián)盟兩種戰(zhàn)略。真虹[6]闡述了港口柔性化的重要性，提出港口應與航運公司和超越傳統(tǒng)運輸功能的中間商等組成戰(zhàn)略聯(lián)盟，保持港口的貨流更加穩(wěn)定。王諾[7]認為港航聯(lián)盟和港際聯(lián)盟成為了第四代港口的主要特點。Song和Panayides[8]基于合作博弈論，通過港口和承運人的實例定量研究了班輪運輸聯(lián)盟。顧波軍、張祥[9]運用博弈論分析了港航合作的最優(yōu)計策，并求解出博弈均衡時港口、船公司和系統(tǒng)的可行解，闡明了存在理想的能被雙方都接受的方案。雖然國內外有一些文獻對港航戰(zhàn)略聯(lián)盟進行了研究，但相對比較冗雜，且不成體系，多從理論角度或運用博弈論進行分析，沒有從根本上解決港航企業(yè)聯(lián)盟的運行效率問題。

關于協(xié)調問題的研究，Malone等[10]認為在供應鏈系統(tǒng)中，優(yōu)化目標在不同個體和系統(tǒng)整體之間存在著明顯的沖突，因此供應鏈是需要協(xié)調的系統(tǒng)。Thomas等[11]將供應鏈協(xié)調歸納為在庫存-分銷、生產-分銷、買-賣方面的協(xié)調。張青山等[12]歸納總結了企業(yè)聯(lián)盟在動態(tài)環(huán)境下的基礎和要素，并討論了聯(lián)盟協(xié)調管理的方法。周永強[13]對供應鏈協(xié)調方法模式進行了探究，根據供應鏈節(jié)點企業(yè)間的合作緊密程度，將供應鏈協(xié)調方法進行了分類。協(xié)調問題大多基于供應鏈管理，局限于對實際問題進行抽象和簡化。可以看到，現(xiàn)有的研究在解決聯(lián)盟具體實施方案的制定與優(yōu)化方面仍然存在一定的局限性。目前少有文章基于聯(lián)盟主體伙伴關系的視角下考慮港、航企業(yè)聯(lián)盟的穩(wěn)定，并未深入探討縱向聯(lián)盟對港航企業(yè)收益、成本的具體影響。而尚未發(fā)現(xiàn)專門針對港航縱向聯(lián)盟，研究船期協(xié)調問題對港航公司收益影響方面的相關研究成果。

因此，本文綜合縱向聯(lián)盟、港航聯(lián)盟和協(xié)調問題等理論，在研究縱向聯(lián)盟下港、航企業(yè)船期協(xié)調時，考慮了眾多影響因素，基于聯(lián)盟博弈理論，分別以航運公司和港口企業(yè)各自的收益最大為目標，建立了船舶的到、離港時刻協(xié)調問題的優(yōu)化模型，并采用考慮量子行為的NSGA-II算法進行求解。最后，以某一航運公司為例，利用本文模型和算法進行求解優(yōu)化，取得較好結果。

2 模型建立與求解

2.1 問題描述

在聯(lián)盟中，船期計劃的協(xié)調是港、航雙方之間常見的談判協(xié)商活動，其結果的優(yōu)化程度將直接影響雙方的經濟效益。一般而言，航運公司為了獲得更大的收益，通常會適當降低船舶航速來減少油耗，節(jié)約其營運成本。但在上下游港口確定的運輸時限下，增加航行時間勢必會縮短船舶的在港時間，對船舶的靠、離泊作業(yè)效率提出更高的要求。而港口為了降低作業(yè)成本，往往會希望船舶在港時間盡可能寬松，從而減少岸橋、集卡等設備的作業(yè)強度，進而節(jié)約裝卸成本。這就使得雙方在船舶靠離泊時間的選擇上可能會產生一定的矛盾沖突，對雙方的聯(lián)盟產生不利影響。本文僅為談判雙方提供決策支持技術，求出可令港航企業(yè)都能接受的最優(yōu)解。

2.2 模型構建

2.2.1 條件假設。為求解該問題，本文做如下假設：

（1）各航線在此港口的貨物裝卸量已知；

（2）決策主體都以自身收益最大化來決策；

（3）在裝卸過程中，分配給船舶作業(yè)的岸橋數以及具體的岸橋不變；

（4）港口的泊位岸橋資源有限；

（5）每艘船舶的裝卸量在數個岸橋之間分布相同；

（6）任意時刻港口正在服務的岸橋數量均不超過碼頭前沿配備的岸橋總數量；

（7）船舶不影響港口原有其他船舶的作業(yè)計劃；

（8）若未達到其中一方的預期收益，港航雙方的收益為0。

2.2.2 模型參數

（1）參數

I：計劃期內到港船舶集合；

i：航運公司的任意船舶，i'為除i以外的船舶，i≠i′且i，i′∈I；

B ：碼頭的泊位集合，j∈B，j為港口的集裝箱泊位；

sud：上游港到下游港的距離；

su：上游港到聯(lián)盟港口的距離；

sd：聯(lián)盟港口到下游港的距離；

rp：基本運費率，取考慮所有掛靠港情況下的平均值；

qi：經過該港口的航段上，對集裝箱貨物的平均貨運需求預測量；

rL：港口的裝卸費率；

Gi：港口管理費；

p：燃油價格；

eL：岸橋的裝卸效率；

vi：船舶i的實際航速；

vei：船舶i的經濟航速；

ui：船舶i每海里的燃油消耗，與航速有關；ui=gi(vi)代表燃油消耗率與速度的關系，具體可根據不同船舶的船型資料得出。

dtui：船舶i離開上游港的時刻；

atdi：船舶i到達下游港的時刻；

c1：每臺岸橋作業(yè)的啟動成本；

c2：岸橋每小時的作業(yè)成本；

Qi：分配給船舶i的岸橋數；

P1：航運公司的預期收益，其中包含船舶的固定成本。

P2：港口企業(yè)的預期收益，其中包含港口的固定成本。

（2）決策變量

ati：船舶i的計劃到港時刻；

dti：船舶i的計劃離港時刻；

xij：0-1變量，若船舶i分配泊位j時 xij=1，否則為0；

（3）從屬變量

f1：航運公司的收益；

f2：港口企業(yè)的收益；

2.2.3 模型建立（1）航運公司收益最大。為方便計算，本文中的在港時間主要考慮船舶的計劃到港時刻和計劃離港時刻。航運公司總收入為向貨主收取集裝箱運輸的總費用。船舶成本主要包括：①燃油費用，與航速有關；②港口成本，若掛靠此港口且能安排作業(yè)計劃時，則會產生相應的裝卸費和固定掛靠費用。因此，以航運公司的收益最大化為模型的目標函數如下：

式（1）表示航運收入減去船舶的燃油費和港口成本的差最大；其中第一項為航運收入，第二項為掛靠此港口時的燃油費，第三項為出現(xiàn)船舶不能靠泊將進行“甩港”操作時的燃油費，第四項為掛靠港收取的費用；式（2）表示航運公司的收益必須不低于其預期收益時才進行聯(lián)盟；為簡化計算，全面考慮船舶的各項成本，預期收益中涵括了船舶的固定成本；式（3）為船舶的航速限制；式（4）表示船舶實際航速與是否掛靠港口、航程距離、船舶的到離港時刻以及經濟航速的關系；式（5）和式（6）分別表示在運輸時限下，船舶的到離港時刻應滿足最早到港時刻和最晚離港時刻的約束。

（2）港口收益最大。港口的核心業(yè)務是服務班輪，提供靠泊、裝卸、倉儲等多方面業(yè)務，為簡化計算，本文中的港口收入主要包括：①提供裝卸服務的收入；②港口管理收入，包括港口企業(yè)按相關規(guī)定向船舶收取船舶噸稅、引航費、停泊費等。船期會影響港口的泊位岸橋調度計劃，因此港口成本主要考慮岸橋成本，包括船舶作業(yè)岸橋啟動成本和裝卸作業(yè)成本。本文以港口的收益最大化為模型的目標函數如下：

式（7）表示港口的裝卸收入與管理收入減去岸橋成本的差最大，即港口收益最大；式（8）表示港口的收益必須不低于其預期收益時才進行聯(lián)盟，為簡化計算，全面考慮港口的各項成本，預期收益涵括了港口的固定成本；式（9）表示每艘船舶會出現(xiàn)靠泊一次或者不能停靠港口這兩種情況[14]；為簡化計算，船舶不能靠泊時將進行“甩港”操作，航運公司重新計劃與安排航線，本文不進行過多贅述；式（10）保證每個泊位最多只能停靠一艘船舶[15]；式（11）保證停靠同一泊位上的船舶處于不同的裝卸作業(yè)時間范圍[16]；式（12）表示船舶完成裝卸任務后才可離港；式（13）表示船舶i可配置的岸橋數量限制；式（14）為模型中的變量取值。

3 考慮量子行為的NSGA-II算法的模型求解

由上述可知港航雙方的收益存在明顯的矛盾，基于縱向聯(lián)盟的港、航企業(yè)間船期協(xié)調是一個典型的多目標優(yōu)化問題。處于相互競爭狀態(tài)的多個目標通過決策變量發(fā)生關聯(lián)，因各目標具有不同的單位和屬性，且考慮相互間的競爭和復雜性，所以客觀地評價多目標問題的解是十分困難的。因此，本文選擇考慮量子行為的NSGA-II算法來進行求解。

3.1 染色體編碼

根據決策變量的特點，本文采用實數編碼方式。為保障種群的多樣性，采用隨機生成的方式，生成長度為3n的染色體，每n位基因分別代表了船舶的到港時刻、離港時刻和停靠的泊位。如圖1中1#所示，代表船舶將會掛靠港口，在計劃周期內第15h到達港口，第29h離港，安排停靠在泊位3。根據染色體編碼的規(guī)則，隨機地生成滿足約束條件的初始種群。

圖1 染色體編碼方式

3.2 適應度函數

多目標問題難以直接確定適應度，本文利用非支配排序對種群進行分層，并給種群中的個體賦以虛擬適應度值。本文尋求航運公司和港口的收益最大化，為雙目標函數。設F1(x)，F(xiàn)2(x)，…， Fm(x)為目標函數值，則適應度函數可表示為

3.3 遺傳過程

在進行遺傳操作時，按照事先給定的交叉概率Pc在種群中篩選出N*Pc個個體。本文交叉操作采用多點交叉算子，具體操作為在個體編碼串中任意地設置多個交叉點，接著再進行基因交換。

本文變異操作結合了均勻變異算子和高斯變異算子[17]，假設有一個個體為X=X1X2...Xk...Xn，假定Xk為變異點，在[UminkUmaxk]范圍內進行取值。在該點進行變異操作后，形成一個新的個體

3.4 量子行為

NAGA-II算法采用的精英策略確保了優(yōu)秀的解能夠進入下一代，但在較高緯度上會出現(xiàn)精度不高的問題，使獲得的非支配曲線容易遠離真正的Pareto最優(yōu)曲線。為解決此問題，本文提出考慮量子行為的NSGA-II算法。

4 算例分析

4.1 背景及數據

（1）某航運公司A計劃掛靠港口P，假設A的5條班輪航線將經過P，且所有航線的上下游港口的船期已定（見表1），每條航線上配備了1艘集裝箱船來提供一個周班服務。每條船的裝卸量已知，平均基本運費率rp=400USD/TEU，船舶的最小限制航速為12節(jié)，最大限制航速為24節(jié)，經濟航速為18節(jié)，港口收取的管理費Gi為500USD/次，燃油價格p設為200USD/t。船舶的燃油消耗率與速度的關系[16]滿足：

（2）假設碼頭屬于離散型泊位布局，擁有4個泊位（1、2、3和4），岸橋作業(yè)效率eL為35TEU/h，每臺岸橋的啟動成本c1為140USD，岸橋每小時作業(yè)成本c2為40USD，由于船長的限制，每個泊位配置的岸橋數最多不能超過5臺，最少不能少于1臺，港口的裝卸費率rL為80USD/TEU。計劃周期為168個單位（即一周，共168h）。在進行泊位岸橋調度之前，碼頭已有10艘集裝箱船的到離港基本信息，見表2。

表1 5條航線時航運公司船舶的航行計劃

表2 港口現(xiàn)有到港船舶的船期表

4.2 算例求解

本文利用MATLAB R2018b進行編程，在配置為2.81GHz Intel(R)Core(TM)i7-7700HQ CPU，8GB內存的環(huán)境下運算。初始種群規(guī)模為200，交叉概率為0.5，變異概率為0.1，最大迭代次數為200。

為了減少誤差及偶然性，本文設置不同的航線數（見表3）、不同的上下游到離港時刻（見表4）以及裝卸效率為28TEU/h三種情形，研究船期計劃對港航雙方利益的影響。通過計算得到三種情形下滿足要求的Pareto解集（見表5）。

表3 不同航線數下的船舶航行計劃

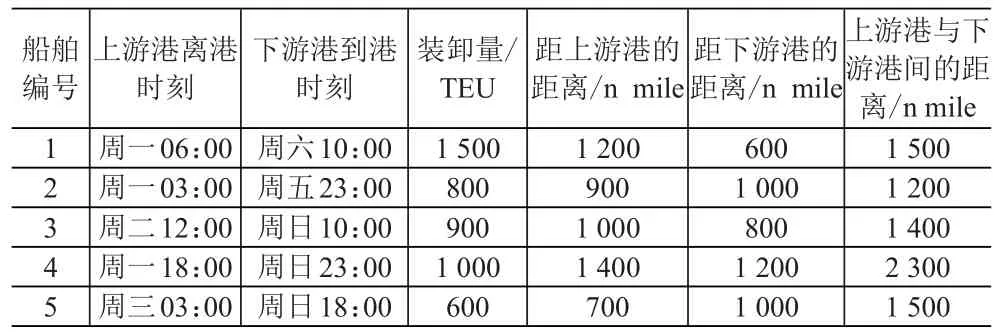
表4 不同的上下游到離港時刻下的船舶航行計劃

表5 不同航線數、不同上下游到離港時刻、不同裝卸效率下的Pareto解集

表5的結果表明，以5條航線時為參照，當航線數增加為6條時，港航雙方的整體收益均有增加，港口收益增長率普遍高于航運公司。當改變航線的上下游到離港時刻時，可供選擇的船期計劃更多，航運公司的收益整體呈現(xiàn)增長趨勢，但港口的收益變化不大。當港口的裝卸效率降低時，港口和航運公司的收益相對都減少了。

航線數為5時，方案1（見表6）是航運公司收益最大時的方案，方案11（見表8）是港口收益最大時的方案。算例中計劃期為一周，通過比較方案1與方案11中港航雙方的收益變化，航運公司、港口企業(yè)的收益極差分別為73 600美元、1 400美元。港口收益的變化幅度雖小，但每周有很多條船舶掛靠港口，可知算例設計符合常規(guī)情況，仍在合理范圍內。

考慮港航聯(lián)盟的背景，港航雙方的收益必須滿足各自的預期收益。若根據最終呈現(xiàn)的Pareto解集和決策經驗，航運公司的預期收益為102萬美元，則航運公司將不愿選擇方案11，這可能會和港口的意愿相悖；當港口能接受的最低收益為37.8萬美元，港口將會拒絕接受方案1、方案2，這與航運公司的選擇意愿產生沖突，在這兩種情況下，港、航企業(yè)將不進行聯(lián)盟。綜合考慮下，方案5可作為理性決策者的參考方案，航運公司收益為106.44萬美元，港口收益為37.835萬美元，該方案的具體船期表安排見表7。方案1中每條船舶配置的岸橋數都趨近于最大岸橋數，增加了港口的成本，船舶在港時間較短；方案5相較于方案11，航運公司收益增加，港口收益卻出現(xiàn)損害，此外方案11中船舶在港時間較長，意味著需提高船舶的航速，增加了航運公司的成本，減少了其利益空間。從經營投資的角度，若在方案5情況下，港航企業(yè)選擇投資經營型的合作模式，航運公司通過參與港口的日常經營管理，獲得優(yōu)質的碼頭服務并能夠加速船舶的周轉，加之在其他業(yè)務層面的合作能夠彌補其損害的部分利益。在上述Pareto非劣解中，決策者可依據各自戰(zhàn)略目標，客觀地選取合適的方案。

5 結論

本文從縱向聯(lián)盟的視角開展港航雙方船期計劃的協(xié)調優(yōu)化問題研究，得出以下結論：

表6 方案1情況下的船期表

表7 方案5情況下的船期表

（1）在縱向聯(lián)盟環(huán)境下，分析了船期計劃對港、航企業(yè)效益的影響，表明船期安排直接關乎港、航企業(yè)的經濟效益。在上下游港口確定的運輸時限下，船期會影響船舶的航速和燃油費用、港口岸橋的使用數量和使用成本，港航雙方的收益存在明顯的矛盾。船期協(xié)調問題實則是港、航企業(yè)合作博弈問題的體現(xiàn)。

（2）本文從博弈論的角度出發(fā)，在考慮港口因素、航運公司因素以及聯(lián)盟博弈的基礎上，以航運公司和港口企業(yè)各自收益最大為目標，建立混合整數非線性規(guī)劃模型，為港、航企業(yè)間船期作業(yè)組織計劃協(xié)調的決策提供一定的參考。此模型為典型的雙目標優(yōu)化問題，為求解該模型，本文采用NSGA-II算法。在求解模型的過程中，由于NSGA-II存在局部搜索能力較弱的問題，因此設計了考慮量子行為的NSGA-II算法。

（3）本文設置不同的航線數、不同的上下游到離港時刻以及裝卸效率變化這三種情形，借助Matlab語言編寫程序代碼對算例進行了求解，分析Pareto解的變化。結果表明所提出的算法能夠在合理的時間內給出相對較為優(yōu)化的Pareto解集，港航雙方可以根據各自實際情況選取合適的船期組織方案。