溫度概念中的物理學思想方法*

吳 英 何應虎 馮景華

(遵義師范學院物理與電子科學學院 貴州 遵義 563006)

溫度是物理學中一個非常重要的物理量.溫度概念的形成經過了漫長的歷史過程,在溫度概念形成的過程中體現了豐富的物理學思想方法.

1 概念的建立見抽象概括

抽象是在思想上抽出各種對象和現象的共同的、本質的特征，舍棄其個別的、非本質的特征的過程.概括是人腦把抽象出來的事物間共同的本質特征綜合起來，并推廣到同類事物中去的過程.概括是一種特殊形式的綜合，是概念形成的重要基礎[1].溫度概念的形成過程就是一個抽象、概括的過程.

最早人們對溫度的認識是從直感出發，憑主觀感覺來測定冷熱程度.從“冷熱程度”到“冷熱程度的科學化”，再到“溫度”，經歷了漫長的抽象概括過程，是人類長期科學活動的結晶.19世紀在熱力學建立的過程中，也是憑經驗將溫度的概念直接引入到理論中，在研究熱力學系統的狀態函數與熱力學基本定律的對應關系時才發現，在確立熱力學第一、第二、第三定律的過程中，已經直接或間接地使用了熱平衡定律，因此1927年美國的物理學家否勒提議將熱平衡定律列為熱力學第零定律[2].根據熱力學第零定律，以任意3個系統A,B,C為例，若A,B分別與C熱平衡，則A和B也處于熱平衡.即一切互為熱平衡的系統都具有某種共同的宏觀性質.這種“共同的宏觀性質”抽象成什么呢？既然是共同的性質，說明互為熱平衡的系統就具有這種共同的性質，同時要判斷系統是否處于熱平衡，只需這一共同性質相同，其他的宏觀性質是不能直接進行比較的.這一宏觀性質就由一個態函數來描述.假設3個系統可以用狀態參量x,y確定，當系統A,C處于熱平衡，描述它們的狀態參量就要被一定的函數關系所制約，寫成函數形式既有

fAC(xA,yA;xC,yC)=0

(1)

同理系統B和C處于熱平衡，有

fBC(xB,yB;xC,yC)=0

(2)

由兩式解出

yC=gAC(xA,yA,xC)

(3)

yC=gBC(xB,yB,xC)

(4)

則

gAC(xA,yA,xC)=gBC(xB,yB,xC)

(5)

要想式(1)和式(5)同時成立，式(5)中可以消去xC,即

φA(xA,yA)=φB(xB,yB)

(6)

因為A,B,C互為熱平衡，可得

φA(xA,yA)=φB(xB,yB)=φC(xC,yC)

(7)

由此互為熱平衡的3個系統都具有一個數值相等的態函數.這個態函數我們用符號T來表示，則3個系統分別有

TA=φA(xA,yA),TB=φB(xB,yB),TC=φC(xC,yC)

(8)

這個態函數就是溫度[3].描述系統的狀態參量x,y即為壓強p和體積V.對于氣體而言，既然確定狀態的參量有壓強和體積就夠了，溫度這個態函數的引入，并沒有增加給定系統的狀態參量的個數，溫度是狀態參量壓強和體積的函數.對于真實氣體而言，這個函數(關系)就是范德瓦爾斯方程

當我們將描述處于熱平衡的系統具有的態函數抽象為溫度后，人類繼續對溫度、壓強、體積這些描述系統宏觀性質的物理量進行概括.在概括的過程中人類對溫度這個概念更加清晰.溫度作為描述系統內在性質的物理量，它的一個顯著特點就是兩個溫度不能相加.兩個溫度之間只有相等或不相等的關系.在熱力學中這類與系統質量無關的物理量叫做強度量.壓強和溫度一樣，都是強度量.但體積就與系統的質量有關，這類物理量叫廣延量.氣體的內能和熵卻是“廣延量”而非“強度量”[4].

2 溫度的測量見分析綜合

分析是頭腦中把事物整體分解為各個部分、各個方面或各個特征.綜合是在頭腦中把事物的各個部分、各個方面或各個特征、各個屬性綜合起來，了解他們之間的聯系和關系，形成一個整體.分析和綜合是思維的基本過程[1].溫度的測量體現了分析和綜合兩種物理學思想方法.

大家都認為溫度是一個可測量.但實際上我們測量的是其他的可測量,然后依賴一個我們未明說的、有時甚至是測量人根本不知道的某個物理學定律，從而得到溫度的數值[5].這些其他的可測量可以是體積壓力(膨脹式溫度計)、聲速(聲學溫度計)、折射率(折射率溫度計)、介電常數(介電常數溫度計)、電阻(電阻溫度計)、熱電勢(熱電偶溫度計)、熱輻射能量(全輻射溫度計)等等.這些溫度計中，溫度計與被測溫物體相接觸，利用熱平衡定律，測量出與溫度緊緊相關的物理量，再通過“綜合”得到溫度的數值，叫接觸式溫度計，如膨脹式溫度計.溫度計與被測溫物體不相接觸，如輻射溫度計，利用傳感器(探測器)將物體輻射的能量轉換成隨溫度而變的光電信號，并由配套儀器將此信號按溫度單位顯示，這種溫度計叫非接觸式溫度計.無論接觸式還是非接觸式，都要通過分析找到溫度與被測物理量之間的關系，最后通過綜合得到被測物體的溫度.

以膨脹式溫度計為例，膨脹式溫度計是以物質的熱膨脹性質與溫度的物理關系為基礎制作的溫度計.按照制造溫度計的材質，膨脹式溫度計可以分為液體膨脹式溫度計(如玻璃液體溫度計)、氣體膨脹式(如氣體壓力式溫度計)和固體膨脹式(如雙金屬式溫度計).首先找到體積、壓力或金屬偏轉角等物理量與溫度的關系，再通過測量這個物理量(體積、壓力或金屬偏轉角等)從而“測量”出溫度.以玻璃液體溫度計為例，首先找到體積變化與溫度變化的關系Vt=V0(1+βt),其中β表示溫度變化1 ℃引起的物質體積變化與它在t℃時體積之比，叫平均體積膨脹系數.Vt是t℃時的體積，V0是0 ℃時的體積[6].通過測量體積的變化Vt-V0，得到溫度的變化t-0,即“測量”得到溫度.

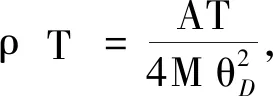
3 溫標的發展見質疑釋疑

概念形成的過程是不斷提出假設、驗證假設的過程.概念所包含的屬性越多，越復雜，假設檢驗的次數就越多，探索的過程就越長[1].為了定量地描述溫度，必須具有能衡量溫度高低的方法，能用來表示溫度數值的方法稱為溫標.溫標的發展經歷了經驗溫標、熱力學溫標、國際溫標建立的過程，體現了質疑、提出假設、驗證假設、釋疑的過程.

早期溫標起源于溫度計的制造，1592年伽利略根據氣體熱膨脹現象制造的溫度計只能定性地表示溫度的高低，所以只能叫感溫器.溫度計怎樣才能定量地描述溫度的高低呢？1641年費狄南、1694年哈克、1665年波意爾、1667年瑪格羅蒂、1694年雷納爾蒂尼、1701年牛頓以及1730年列莫等人都提出了建立定量描述溫度高低的方法，后人稱之為經驗溫標.其中1714年華倫海特用冰水混合后的溫度為32度，水的沸騰溫度為212度,中間均勻地分成180格，每一格為華氏溫標1度(℉),稱之為華氏溫標；1742年攝爾修斯以冰的熔點為零度，水的沸騰溫度為100度，兩點之間100等分，每一等分為1度(℃)，創立了攝氏百度溫標.這些經驗溫標都有固定的溫度點、表示固定點之間溫度的溫度計、用來確定固定點之間溫度量值的數學關系等三方面的內容，所以,基本實現了定量描述溫度高低的目的.

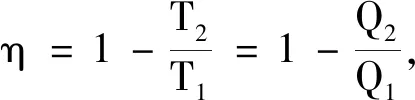
熱力學溫標建立之后，人們發現要想獲得足夠的準確度，構成熱力學溫標的測溫裝置非常復雜，成本昂貴，實驗過程稍有不慎就會誤差很大，復現性很低.能否找到一種國際溫標，由它確定的溫度復現精度高，試驗方法簡單便于溫度量值傳遞，能滿足生產需要，使用的測溫儀器測得溫度與熱力學溫度一致，技術條件能體現當代科學水平，這樣的溫標存在嗎？1887年卡比伊研究制成定容氣體溫度計，建立了氫百度溫標，1899年卡林達爾用鉑電阻溫度計作為溫標的內插儀器，1911年德國柏林技術物理研究所建議采用卡林達爾的設想，1927年在英、美、德三國實驗人員共同努力下，向第7屆國際計量大會提出實用溫標協議草案，這種溫標以百度溫標為基本溫標，以6個可復現的固定點(氧沸點、冰熔點、水沸點、硫沸點、銀和金的凝固點)，3種內插儀器(鉑電阻溫度計、鉑銠10-鉑熱電偶、光學高溫計)、4個內插公式來確定溫度，溫度用℃表示，下限為-190 ℃，計量大會命名其為1927年國際溫標(ITS-27).隨著科學技術的發展，對溫度測量準確度的要求越來越高，ITS-27確定的溫度與熱力學溫度有一定的偏離，在1939年、1948年、1954年、1967年、1975年、1990年，以及今后都需要分別對國際溫標進行修改，使之不斷完善[7].

4 統計解釋見唯象機理

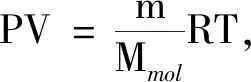
5 正負溫度見比較推理

比較是在思想上把各種對象和現象加以對比，確定它們的相同點、不同點及其關系.比較是一種重要的物理學思維方法.推理是由具體事物歸納出一般規律或者根據已有的知識推出新的結論的思維活動[1].溫度有高溫和低溫，還有超高溫(即金的凝固點1 337.58 K以上的溫域)和超低溫(即氧的露點90.188 K以下的溫域).那正、負溫度的物理意義是什么，正溫度高，還是負溫度高？在正、負溫度概念的建立中體現了比較和推理的思想方法.

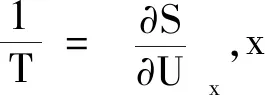
那負溫度是不是比正溫度低呢？溫度是表征粒子在能級上分布情況的物理量.溫度越高，分布在高能級上的粒子數越多.當T→±，兩個能級上的粒子數相等.再吸收熱量，粒子反轉分布，溫度轉變為負值，此時的負溫度是比無窮大溫度還要高的溫度.我們可以對由“冷”到“熱”的順序做一個排列：0+K,…,±K,…,0-K，這個順序和我們的習慣完全不同，我們只需將玻爾茲曼分布函數中定義成一個新的溫度新溫度順序為-→0→+，最冷、最熱分別由-和+來標志，與人們通常的習慣一致了.負溫度在研究激光器及微波激射量子放大器時是一個十分重要的概念，但我們只是將反轉分布與玻爾茲曼分布的數學表達式進行對照而得出的結論，這時整個系統仍然處于正溫狀態，要不然實現負溫狀態的激光器，在比無窮大還高的溫度下，早已不復存在[2].因此在對正負溫度進行比較的過程中，我們更進一步理解，溫度的確標志著系統中粒子熱運動的劇烈程度，這與溫度微觀意義的定性描述也是一致的.

在物理學形成和發展成為一門科學的過程中逐

步形成了物理學的思想方法.溫度作為物理學重要的概念之一，在概念形成和完善的過程中，體現了豐富的物理學思想方法.