利用剛體的平面平行運動證明平行軸定理*

申慶徽 陳 兵

(山東科技大學電子信息工程學院 山東 青島 266590)

平行軸定理是剛體轉動的一個重要知識點, 它反映了剛體繞相互平行的不同轉軸轉動時轉動慣量之間的關系. 在大部分的教材中對該定理的證明都是從轉動慣量的定義出發[1]. 本文從剛體的平面平行運動模型出發, 通過分析運動的動能推出了平行軸定理.如圖1所示, 考慮任意剛體作平面平行運動, 純滾動要求剛體與平面之接觸點在接觸那一瞬間為相對靜止, 沒有任何的相對滑動或滾動, 即相對速度為零, 此接觸點即為速度瞬心. 此時, 剛體可以看成繞通過該瞬心的轉軸轉動, 且轉動的角速度為ω. 設該剛體繞垂直于平面且通過瞬心轉軸的轉動慣量為IO, 則剛體運動的總動能為

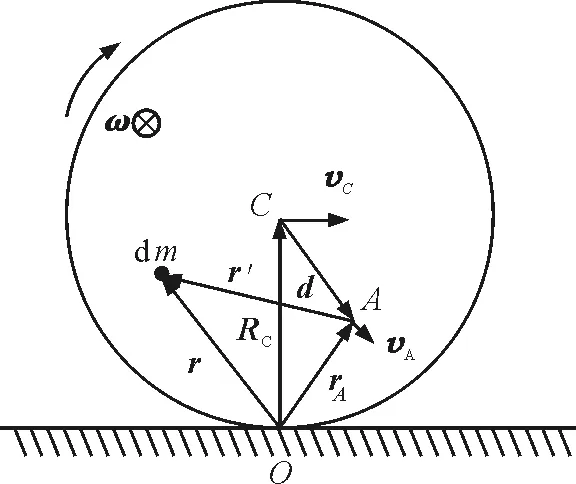
圖1 剛體的純滾動模型

(1)

另一方面, 由柯尼希定理可知剛體平面平行運動的總動能等于質心的動能與剛體繞質心的轉動動能之和[2], 即

(2)

其中,IC為剛體繞過質心C軸的轉動慣量,m為剛體的質量,vC為剛體質心C平動速度的大小. 由于平面平行運動剛體的角速度與相互平行的轉軸位置無關[3],即質心平動的速度

vC=ω×RC

vC=|ω×RC|=ωRC

代入式(2)可得

(3)

對比式(1)和式(3)不難發現

(4)

此即平行軸定理.

上述分析并非只適用于轉動瞬心的轉動慣量與質心轉動慣量之間的關系, 還可以推廣到任意情況. 在圖1中, 考慮任意轉軸A, 設其相對瞬心的位置矢量為rA, 相對于質心的位置矢量為d. 設質元dm相對于O點的位置矢量為r, 根據前面的討論知，質元dm的線速度為v=ω×r. 根據動能的定義

(5)

以A為參考點剛體的動能表達形式可以寫為

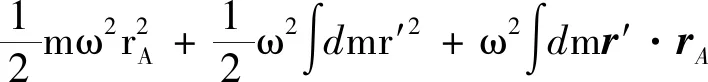
(6)

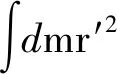
mω2(RC-rA)·rA

(7)

上式等號右邊第一項可以理解為轉軸A的平動動能，第二項表示剛體繞轉軸A的轉動動能，第三項表示對前兩項動能的補償量.不難看出，當rA=RC時即A點與質心C重合，式(7)即為柯尼希定理；當rA=0時,即A點與速度瞬心O重合，式(7)退化為式(1). 此外，比較式(7)與式(3)可得

(8)

整理得

IA=IC+m(|RC-rA|)2=IC+md2

(9)

此即剛體繞任意轉軸A的轉動慣量與質心轉動慣量之間的關系，也就是平行軸定理.