單擺實驗的數值理論分析*

李 群 堯 莉 章世晅

(東華理工大學理學院 江西 南昌 330013)

1 引言

單擺是一種理想的物理模型，由理想化的擺球和擺線組成.在滿足偏角小于等于5°的條件下，單擺的運動近似為簡諧振動，因此，單擺經常作為研究簡諧振動的基本內容[1].當擺角大于5°時，單擺的運動變得復雜，其運動方式也由線性走向非線性[2,3]，大量研究分析單擺運動的論文見諸于各類期刊上[4～8].

單擺實驗作為最基礎的內容在大學物理實驗課程中開設[9,10]，既可作為簡諧運動的方式測定本地重力加速度，也可通過大角擺動的動力學分析作為學習非線性物理的重要基礎.因此，單擺實驗成為連接基礎物理與近代物理(非線性物理)的橋梁，通過單擺我們既能了解最簡單的振動方式簡諧振動，又能通過初始條件的變化學習非線性動力學的知識.

本文通過討論單擺由線性走向非線性的變化，主要方法采用數值理論模擬分析線性諧振動和非線性諧振動的圖像變化；角振幅的變化引起的周期變化以及不同擺長對應的周期變化，通過分析這些條件為單擺實驗中取得理想的結果提供理論借鑒.

2 實驗原理

如圖1所示單擺，小球的質量為m，其質心到懸掛點O的距離為l(擺長).偏離平衡位置θ角時，作用在小球上的切向力的大小為mgsinθ，它總指向平衡點O′.當θ角很小時，有sinθ≈θ，切向力的大小為mgθ.質點動力學方程為

圖1 單擺

(1)

當θ≤5°時，為簡諧運動方程的動力學微分方程，式(1)的通解為

θ(t)=Acos (ω0t+φ)

(2)

(3)

單擺在擺角很小、無阻尼時的擺動為簡諧振動，簡諧振動是一切線性振動系統的共同特性，它們都以自己的固有頻率做正弦振動.

當θ>5°時，sinθ≈θ不再成立，式(1)為

(4)

此時的微分方程不再是線性方程，無嚴格解析解[1,2].

3 簡諧近似和非線性的振動圖像比較

圖2為擺長l=1 m時角振幅分別為3°,10°,30°時的時間(t)-位移(y)圖像，圖中實線為簡諧振動圖，虛線為數值模擬振動曲線圖，點實線為同一時刻兩者差值曲線圖.圖2中可見當角振幅為3°時，數值模擬與簡諧振動曲線吻合得很好，可視為簡諧振動；角振幅為10°時，兩條曲線在很短時間就不再重合，此時已不能視為簡諧振動；角振幅增加至30°時數值模擬曲線已明顯偏離簡諧振動曲線，即大角擺動已非線性諧振動.

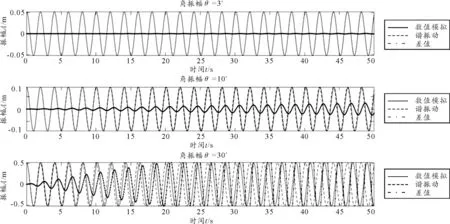
圖2 不同角振幅時的振動曲線

4 大角時的振動周期計算

可得

將上式兩邊積分得

開方后可得

則周期公式

(5)

式中積分上限θm為角振幅，積分下限0即平衡位置.

上式還可寫為第一類完全橢圓積分形式

(6)

4.1 角度的改變與周期的關系

圖3為0～90°對應的周期圖，圖中“*”代表簡諧振動式(2)近似下的周期;“o”表示式(5)數值積分計算不同角度對應周期;“+”表示式(6)第一類完全橢圓積分的計算結果.由圖可以看到數值計算與第一類完全橢圓積分完全重合，兩者重合結果可相互證明方法的正確性.從圖中可知擺角大于10°后與諧振動明顯偏離，此時計算周期不能采用簡諧振動的計算方法.

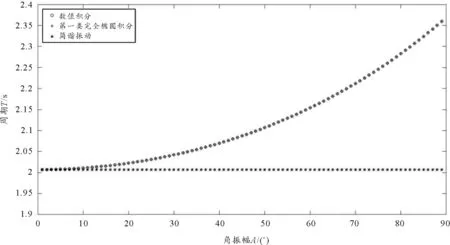
圖3 周期與角振幅關系

4.2 擺長對周期的影響

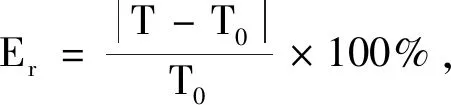
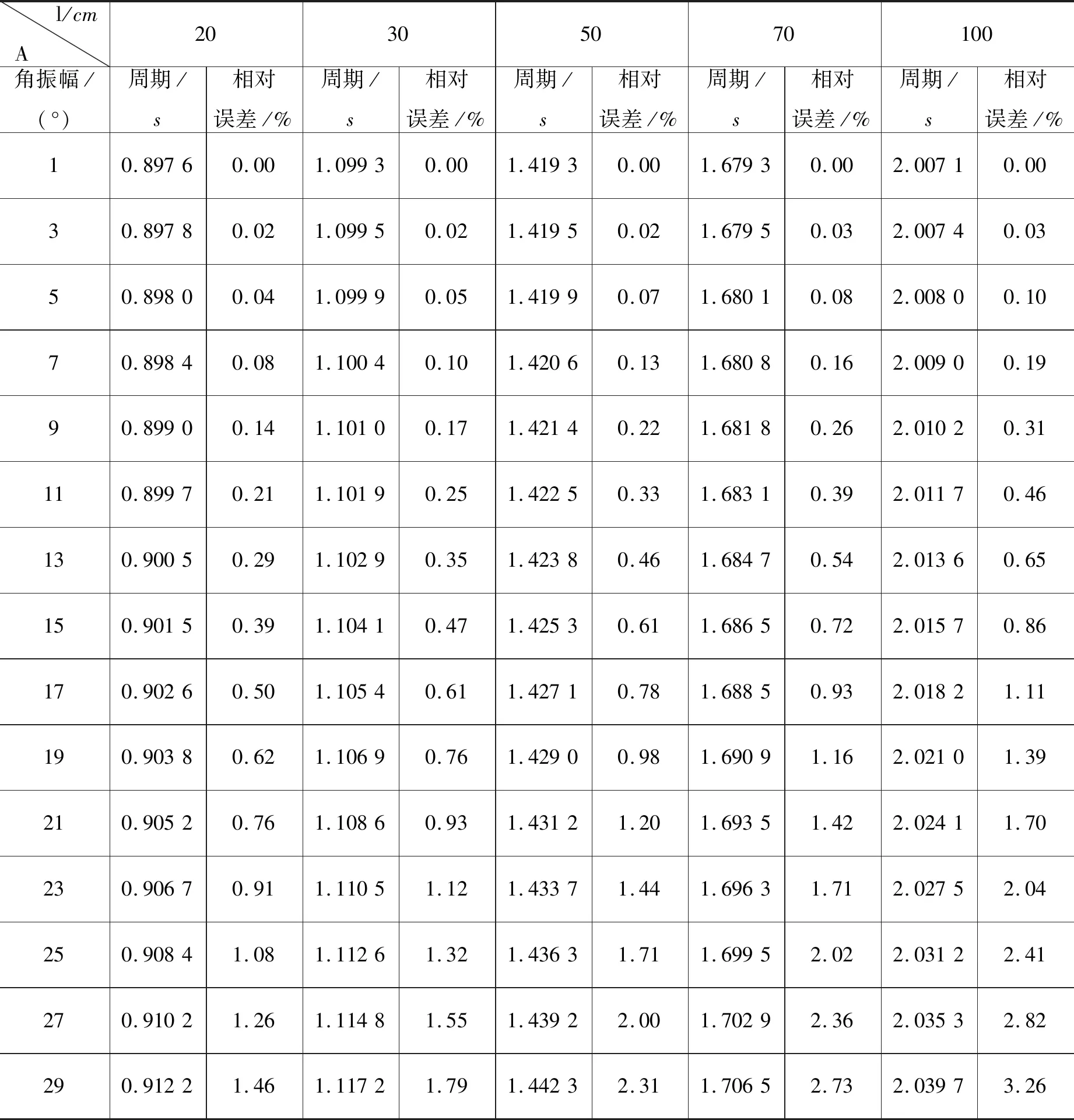
表1 不同擺長的周期及相對誤差

根據表1的統計結果：相同擺角時擺長增加相對誤差也隨之增加，擺長較小時相對誤差也較小.相對誤差在1%內的數據在實際測量時當然可視為較好的測量，由表1可知，如果把1%作為標準的話，擺長為20cm時擺角25°以內都可視為好的測量數據，其誤差在完全可接受的范圍內，隨著擺長增加到100cm時，擺角15°以內的數據都可以算合格數據.當然以上分析的前提為不考慮儀器本身誤差和測量時的不可控的人為引入誤差等.

單擺實驗的實驗者在實際實驗操作時會特別強調小角擺動對實驗結果的重要性，但5°以內的角度在實際操作中很難嚴格控制，從上述分析結果看，可得到結論，只要控制一定的擺角,測量出的周期對實驗結果(重力加速度)影響不大.由表1還可得到另一結論：在擺長遠大于擺錘尺寸的前提下(理想單擺)，擺長不宜過長，否則大角擺動的非線性會影響實驗結果.

5 結論

采用理論(數值)分析的方法對單擺進行研究，結果發現單擺由小角到大角的擺動過程中振動圖像在由線性(小角)到非線性(大角)緩慢變化，角度越大非線性現象越明顯；對周期的計算分別采用第一類完全橢圓積分和數值積分的方法，結果證明周期與擺長、角振幅相關；不同擺長的周期分析，擺長較小時有利于實際實驗測量，其帶來的相對誤差較擺長較大時更小，為實際操作方便和準確測量，角振幅(擺角)的選取可適當增加，對實驗結果不會引入較大誤差.