基于角平分線的無孔復雜多邊形中軸提取算法

黃斌 劉軍 范啟東 唐嘉胤

摘要：中軸可以有效表達多邊形拓撲結構信息，同時可以去除冗余信息，并且具備對局部幾何變形不敏感等特點，吸引了學術界的廣泛重視。但現有的中軸提取方法存在計算資源消耗大，運行速度慢，數據不穩定等問題。本文在現有草火模型及最大圓盤模型的基礎上，提出了一種基于角平分線的無孔復雜多邊形中軸提取算法。該算法利用多邊形凹凸點的偏置處理來獲得中間分支點，然后通過“手擠”方式獲得中軸，并利用邊界的連續性保持中軸的連續性。實驗結果表明該算法能滿足中軸的提取并能保持中軸的連續性，而且減少了自交檢測的復雜程度。

Abstract The central axis has the characteristics of effectively expressing the topological structure and geometric information of polygons， removing redundant information， and not sensitive to local deformation， which has attracted extensive attention of academia. There are many problems in the existing methods， such as large consumption of computing resources， slow running speed， and data instability and so on. In this paper， based on the existing grass fire model and the largest disk model， an algorithm of extracting the central axis of complex polygon without hole based on angle bisector is proposed. The algorithm uses the offset processing of polygon concave and convex points to obtain the middle branch points， then uses the way of "hand extruding" the boundary to obtain the central axis， and uses the continuous topological structure of the boundary to maintain the continuity of the central axis. The experimental results show that the algorithm can meet the requirements of axis extraction and maintain the continuity of the axis， and reduce the complexity of self-intersection detection.

1. 引言

隨著CAD/CAM/CAE的應用日趨廣泛及計算機圖形學的不斷發展，利用多邊形對數字模型進行表達的方式在實際應用中越來越多。但該表達方式會隱藏模型的關鍵信息，不利于拓展模型的應用。另外，數字模型通常蘊含巨大的數據量，對模型上所有數據進行操作，如重建運動場景，分析結構受力，規劃加工路徑等，對于大多數硬件設備都是一個巨大的挑戰[1-3]。對于數量級巨大的多邊形模型，如果要以常規硬件實現大數據處理，就需要將模型的結構信息濃縮，并從中提取核心數據，然后以現有硬件進行有限數量級別操作，最后將操作數據逆向重建，實現數量巨大的多邊形模型處理。

結構信息濃縮概念在日常生活中并不少見，例如人類肢體及機械結構的運動簡圖。人類運動可以看成是忽略神經系統和肌肉細胞控制作用的骨骼運動;而機械結構也可以將復雜的零件特征簡化為抽象線框。因此，結構信息濃縮的概念也可以用于將多邊形模型濃縮為抽象的骨架線框。從多邊形中抽取出的骨架線框，學術界將其定義為多邊形中軸。多邊形中軸由于包含著豐富的幾何機構信息，可以直接應用于科學工程領域，包括地理信息系統、人臉識別、圖像處理、計算機視覺和機械結構分析等[4]。

多邊形中軸的提取模型主要有兩種：草火模型和最大圓盤模型。草火模型是假設圖形的邊界同時點火，火源向圖形內部各個方向等速燃燒直至熄滅，熄滅點形成的點集為多邊形的中軸[5];而最大圓盤模型是指平面幾何圖形中的中軸是內切于幾何圖形邊界至少兩個或兩個以上等距離的點的軌跡[4]。

多邊形中軸具備有效表達多邊形的拓撲結構和幾何信息，同時可以去除冗余信息，并且對局部變形不敏感等特點，吸引了學術界的廣泛重視。而中軸提取更是眾多研究學者關注的焦點，合理快速的中軸提取算法一直是學術界及工業界追求的目標。本文將在草火模型和最大圓盤模型的基礎上提出一種基于角平分線的改良中軸提取算法。

2. 相關工作

目前對多邊形中軸的提取方法都是基于草火模型和最大圓盤模型，常用的中軸提取方法包括有形態學細化法[6]、拓撲邏輯瘦身法（topological thinning）[7]、距離變換法（distance transform/DT）[8]、草火法（simulations of grassfire propagation）[5]、泰森多邊形法（Voronoi diagram）等[9]。而從計算精度來看，眾多的中軸提取方法大致可以分為精確算法和逼近算法兩類[12]。

精確中軸提取算法包括形態學細化法、拓撲邏輯瘦身法、距離變換法等。形體學細分法屬于圖像處理范疇，通過膨脹、腐蝕、開閉運算、擊中或擊不中變換、細化、骨架及重構對象等一系列運算獲得最終的中軸圖形[1]。形態細化法最常用的就是最大圓盤法[6]，通過多邊形內所有最大圓盤的圓心提取多邊形的中軸，但存在著連通性不佳的缺點。拓撲邏輯瘦身法[7]是在形態學細化法的基礎上發展出來的中軸提取方法，通過逐步去掉簡單點（不影響拓撲性質和形狀的點）而獲得中軸，但其僅能保證在二維空間的正確性。距離變換法是通過尋找距離梯度脊線來形成骨架，該方法得到的骨架位置精確，但難以保證骨架的連通性。但精確中軸提取算法多采用全局遍歷法，存在計算資源消耗大，運行速度慢等問題;另外一些精確中軸提取算法將圖形進行分割成簡單多邊形，然后提取中軸，最后將各部分中軸融合成為最終的總中軸，則在中軸融合時出現準確性不佳及計算復雜等問題。

針對精確中軸提取算法存在的問題，研究人員相繼開發出效率更高的逼近算法。逼近算法主要包括擴展草火法[13]、泰森多邊形法[9]、Delaunay三角剖分法[10]和柵格法等。擴展草火法采用類似草火法的統一方法來定義二維中軸全局形狀度量（EDF）及二維形狀的中心（EMA），并通過厚度腐蝕方法得到圖形的中軸。該方法在修剪中軸、對齊形狀和形狀描述方面的具有一定的實用性。泰森多邊形法[9]將復雜多邊形界線分解成點集，然后通過這些點集構成泰森多邊形圖（Voronoi diagram），泰森多邊形圖在多邊形內的公共邊即是多邊形的中軸，但該方法依賴于規模或密度。Delaunay三角剖分法[10]利用Delaunay三角剖分的空球特性（平面上是圓），對邊界點集細化，以提取多邊形的中軸。柵格法[11]則通過最近邊緣點集距離的均值變換，結合新的中軸點判定規則，利用種子點生長判別法提取曲邊多邊形的中軸。但基本上使用逼近中軸提取算法均存在數據提取不穩定的缺點，迄今為止還沒得到很好的解決。

3. 理論算法

針對上述精確及逼近中軸提取算法的不足，本文利用結合角平分線的概念及多邊形邊界拓撲連續性，實現無孔復雜多邊形的中軸提取。無孔復雜多邊形的中軸提取的理論主要分為以下四個基本算法：多邊形凹凸判斷算法，凸多邊形偏置算法，非凸多邊形 偏置算法，及中軸重構算法。

3.1 多邊形凹凸判斷算法

要從復雜的封閉多邊形進行中軸提取，首先要定義一個實體方向的概念。

多邊形實體方向定義（如圖1）：

多邊形的邊界線段是有向線段或多段線。

有向線段或多段線的前進方向的左側為實體，則該線段或多段線的前進方向為多邊形的實體方向。

要確定多邊形的凹凸性。在各種多邊形中軸定義模型中，多邊形的輪廓實體方向的凸點存在中軸，凹點不存在中軸;但凹凸點也會影響中軸的位置，因此需要對多邊形的凹凸性進行判斷。

多邊形頂點凹凸性判斷方法主要有角度法、左右點法、矢量面積法、向量積法、射線法和極點順序法等[14]，這些算法基本上是等效的。本文采用的是向量積法來判斷多邊形頂點的凹凸性。如圖1所示，邊界ABC（C）的左側為實體，頂點C位于矢量線段AB的左側，則計算向量AB和向量BC的外積，外積公式采用：

向量BD的單位向量與z軸的正方向相同，這時多邊形的頂點屬于凸頂點。而對于頂點C而言，其位置位于矢量線段AB的右側，向量BD的單位向量與z軸的正方向相反，這時多邊形的頂點屬于凹頂點。

由于多邊形的輪廓上有多個頂點，因此必須采用歷遍法對各個頂點進行凹凸性判斷，并最終確定多邊形的凹凸性：若全部頂點均為凸頂點，那么，該多邊形為凸多邊形;反之，若多邊形上存在一個或以上的凹頂點，該多邊形為非凸多邊形。

3.2凸多邊形偏置算法

草火模型和最大圓盤模型均采用其描述方式對多邊形的中軸進行定：草火模型采用的是由外至內的距離延伸方法，而最大圓盤模型采用的是相反的由內至外的距離延伸方法。通過比較兩種定義方法，可以發現其最終的目標都是在尋找距離相等的點或線段。而在平面幾何學中，角平分線的性質就剛好滿足這一要求，如圖2。林福嚴等[15]利用這角平分線的性質提出了一種平面凸多邊形中軸提取方法，但該方法的判據并未考慮多邊形的特殊情況。而這里提出的凸多邊形偏置算法是在林福嚴等提出的方法上進行改良，將多邊形的特殊情況也進行考慮。

凸多變形偏置算法描述如下：

步驟1：尋找凸多邊形的最小厚度。

（1） 按凸多邊形實體方向獲取各頂點的坐標，然后計算每一個頂點的角平分線的單位向量，求出兩頂點間線段與兩頂點法向量所構成的三角形的高（圖3）。三角形的高的計算公式如下：

（2） 比較凸多邊形上所有輪廓線段對應三角形的高，尋找最小值，作為多邊形的最小厚度。凸多邊形頂點角平分線與頂點簡單的多邊形輪廓線段構成了三角形，三角形對應高的最小值選擇方式如下：

（3） 求出最小厚度所在的三角形上由兩多邊形頂點角平分線構成的頂點坐標，作為中軸線的中間分支點。計算方式如下（以圖2為例，A為第一個中間分支點）：

步驟2：尋找第一個無自交的凸多邊形環。

（1） 按凸多邊形實體方向對每個頂點角平分線進行截點計算。計算方式如下：

（2） 按凸多邊形頂點的拓撲關系對截點進行連接，構成了一個新的凸多邊形（圖4）。由于最小厚度所在三角形對應的凸多邊形輪廓線段已退化成一點，如圖7的V1、V2兩點退化成P1點，新凸多邊形的邊數為N-1。

圖4利用截點的拓撲關系形成新的凸多邊形。

步驟3：找出所有中間分支點。 重復步驟1和2，找出所有無自交的凸多邊形環及所有的中間分支點，直到多邊形上所有頂點退化到一點。這時，中間分支點到其對應的多邊形輪廓線段的距離為多邊形在該輪廓線段上的最大厚度。

3.3非凸多邊形偏置算法

凸多邊形僅是多邊形中的特例，而實際上更多存在的是非凸多邊形。非凸多邊形的偏置算法長期以來都是以一個難以解決的問題，而問題關鍵是在于如何處理非凸多邊形輪廓在偏置后出現的自交現象。自交現象產生的原因是由于偏置距離設置與輪廓線拓撲結構的相互影響而產生的，如圖5。正常情況下，輪廓ABCD在偏置d1距離后會生成偏置曲線ABCD，如圖5（a），但若偏置距離過大時，輪廓ABCD的偏置曲線ABCD在保持原有拓撲結構的情況下會出現AB和CD兩段曲線自交，如圖5（b）這就是自交產生的原因。自交現象的出現會增加中間分支點位置的不確定性。對于這種情況，通常的處理情況是在偏置后對所有線段進行自交檢測，但會隨著多邊形變數的增多，算法的執行效率會降低。針對這種情況，在凸多邊形偏置算法的基礎上，本文通過整合臨界偏置處理，如圖5（c），提出了一種基于非凸多邊形最小厚度的角平分線偏置算法，其核心在于找到偏置處理的臨界點。

非凸多變形偏置算法描述如下：

步驟1：尋找非凸多邊形的最小厚度。

（1） 按凸多邊形偏置算法的步驟1計算出兩頂點間線段與兩頂點法向量所構成的三角形的高。但不同的地方在非凸多邊形上計算出來三角形的高是帶正負方向的，因此，這里規定只有正向的三角形高才是有效數值。

（2） 多邊形凹凸判斷算法找出非凸多邊形輪廓線上的凹頂點，并計算凹頂點的角平分線正方向（從頂點交出發指向多邊形內部方向）與距離最近的輪廓邊界線段的交點。具體方法如下：

尋找跟凹頂點的角平分線正方向相交的輪廓邊界線段。假設角平分線與輪廓邊界線段相交，輪廓邊界線為直線線段，輪廓線段的兩端點必在角平分線的兩側。圖6所示為角平分線與輪廓邊界線段相交的判斷，BQ為多邊形凹頂點角CBA的正向角平分線，與輪廓邊界線段EF交于P點，端點E和F分別位于BQ左側和右側。然后引入相交判斷系數，并進行計算：

為E到BQ的有向距離，

為F到BQ的有向距離，

為的單位向量

為的單位向量

為相交判斷系數。當等于0時，角平分線與輪廓邊界線段相交。

求出交點P的位置。借助有向距離的模及邊界線段端點坐標，可以快速計算出交點坐標。計算方式如下：

為角平分線與輪廓線段的交點坐標

為角平分線與輪廓線段的交點坐標

計算所有與同一凹頂點的角平分線相交邊界線段的距離，找出最短距離，確定最近的邊界線段。

計算凹頂點所在角平分線與相交邊界線段等高的交點，如圖7。計算方法如下：

比較所有凹頂點角平分線及最近輪廓邊界線的等高距離，尋找最小值，

和分別為第個凹頂點角平分線及最近輪廓邊界線的等高距離及最后一個凹頂點角平分線及最近輪廓邊界線的等高距離。

（3） 比較凹頂點等高距離及輪廓邊界線對應三角形的高，尋找最小值作為非凸多邊形的最小厚度.

步驟2：尋找第一個無自交的非凸多邊形環。

（1） 利用式（4）計算非凸多邊形實體方向的每個頂點角平分線上的截點計算。

（2） 按凸多邊形頂點的拓撲關系對截點進行連接，構成了新的多邊形。非凸多邊形在這里會出現兩種情況，第一種情況，輪廓邊界線對應三角形的高為最小值，最小厚度所在三角形對應的凸多邊形輪廓線段會退化成一點，新的多邊形只有一個且邊數為N-1，與凸多邊形偏置的情況一樣。

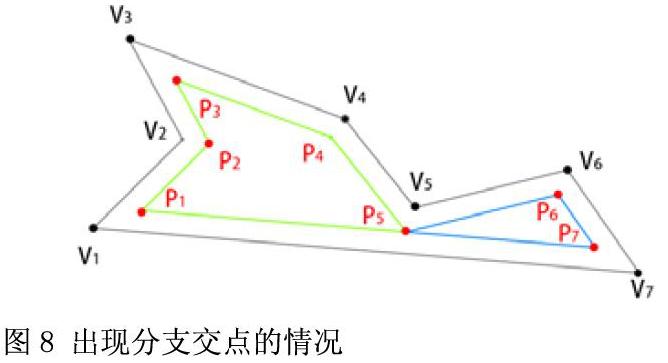
第二種情況，凹頂點等高距離為最小值，凹頂點角平分線正方向上與最近輪廓邊界線段的偏置線段會出現分支交點（圖8），此時，新的多邊形會出現兩個或以上的多邊形。由于分支交點P5既屬于角平分線V5P5上的點，又屬于輪廓線段V1V7的偏置線段P1P7上的點，但實際上偏置線段P1P7上并無P5這點，需要通過插值的方式將P5放到P1P7上以保持多邊形邊界的合法性。分支交點也是非凸多邊形中的中間分支點。

步驟3：找出所有中間分支點。對于分割出來的新多邊形，則對其的多邊形凹凸性進行判斷，然后按照其屬于凸多邊形或非凸多邊形的偏置算法進行處理。如果新生成的多邊形是凸多邊形，則按凸多邊形偏置方法找出所有無自交的凸多邊形環以及所有的中間分支點，直到多邊形上所有頂點退化到一點，如果新生成的多邊形是非凸多邊形，則按步驟1和2 進行操作，找出所有無自交的非凸多邊形環以及所有的中間分支點。偏置操作直至該非凸多邊形中內再無多邊形環可提取。

3.4中軸重構算法

中軸重構算法可分為對兩類：凸多邊形中軸重構算法及非凸多邊形中軸重構算法。而重構算法的關鍵在于保持中軸拓撲結構的連續性。本文提出一種“手擠（Hand Squeeze/HS）”式中軸重構算法，利用輪廓邊界拓撲結構的連續性來保持凸多邊形及非凸多邊形中軸的連續性。

3.4.1 凸多邊形中軸重構算法

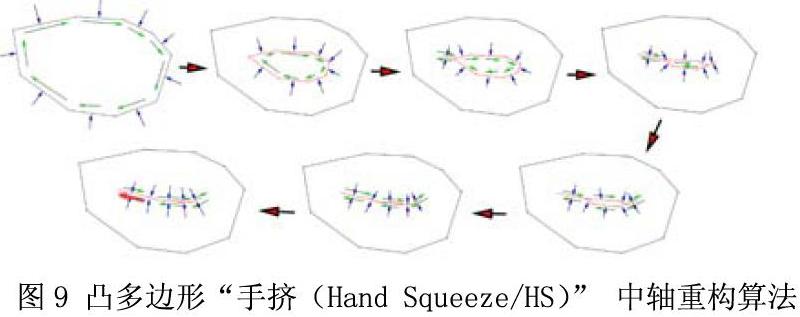
凸多邊形中軸重構算法如圖9， 假設用手握著凸多邊形，然后均勻用力握住凸多邊形。由于手形的生理特征，多邊形較長的方向會與四指彎卷方向呈銳角方向。另外假設凸多邊形的硬度為零，輪廓邊線可以隨意向垂直方向擠壓，并在擠壓過程中，輪廓邊線允許軸向收縮。基于這兩點假設，凸多邊形可以向內部收縮直到輪廓邊線間沒有收縮“空間”，這樣就成為該凸多邊形的中軸。但此時，輪廓邊線間還是連續的。通過這種算法，可以快速得到連續中軸。而這種算法的定義為：

定義1：在頂點偏置過程中保持每個頂點間的拓撲關系，不作任何添加和修改。

定義2：在到達最小偏置距離及出現中間分支點時，允許出現重合點，但仍舊保持輪廓的拓撲連續關系。

定義3：從中間分支點繼續偏置時，假設在“手擠”過程中，物體已經到達“背靠背”的狀態其無法繼續擠壓，從而形成一條直線段。此時，分支點不再移動，其他點仍然向線段的垂直方向“擠壓”。這種情況下，需要在重合點間插入中間分支點并固定，其它點仍沿著頂點的角平分線正方向移動，如圖10。

定義4：繼續擠壓直到所有輪廓邊界線段間沒有“空間”，得到中軸，如圖11。

3.4.2 非凸多邊形中軸重構算法

非凸多邊形中軸重構算法如圖12，與凸多邊形的“手擠”中軸重構算法類似。但不同的是凸多邊形是單手“手擠”壓縮，而非凸多邊形是多手在兩凹點間構成的半凸多邊形進行“手擠”壓縮。非凸多邊形的“手擠”壓縮過程的假設跟凸多邊形一樣，通過均勻施加壓力，擠去非凸多邊形上的冗余空間，得到非凸多邊形的中軸。非凸多邊形的“手擠”壓縮中軸提取的定義如下：

定義1：在頂點偏置過程中保持每個頂點間的拓撲關系，不作任何添加和修改，同凸多邊形中軸重構算法定義1。

定義2：在到達最小偏置距離及出現中間分支點時，允許出現重合點，但仍舊保持輪廓的拓撲連續關系，同凸多邊形中軸重構算法定義2。

定義3：從中間分支點繼續偏置時，到達“背靠背”的狀態，且形成一條直線段。此時，分支點不再移動，其他點仍然向線段的垂直方向“擠壓”。這種情況下，需要分兩種情況。第一種情況，如果是凸頂點形成的中間分支點，處理方式同凸多邊形中軸重構算法步驟3，即在重合點間插入中間分支點并固定，其它點仍沿著頂點的角平分線移動。第二種情況，如果是凹頂點形成的中間分支點，除了將中間分支點固定以外，還需要插入額外控制點，并沿著先出現的角平分線正方向移動（圖13）。

定義4：繼續擠壓直到所有輪廓邊界線段間沒有“空間”，得到中軸，如凸多邊形中軸重構算法定義4。

4. 實驗驗證

對于上述理論，需要通過實驗進行驗證，以下將分別對凸多邊形和非凸多邊形進行實驗。

4.1 凸多邊形

為確保凸多邊形偏置算法的有效性，實驗樣本為隨機一個凸多邊形。在凸多邊形的實驗樣本上，按逆時針順序作各頂點的角平分線，計算出第一個無自交的凸多邊形環的最小偏置距離，利用式（4）求出的中間分支點及第一個無自交凸多邊形環上的控制點，連接成新的凸多邊形（圖14）。然后按3.2凸多邊形偏置算法的步驟3按計算得出的各最小偏置距離進行偏置，直至所有凸多邊形頂點退化到一點。最后中軸提取方法提取凸多邊形的中軸（圖15）。

4.2 非凸多邊形

同樣，為確保非凸多邊形偏置算法的有效性，實驗樣本為隨機一個非凸多邊形。在非凸多邊形的實驗樣本上，按逆時針順序作各頂點的角平分線，計算出第一個無自交的非凸多邊形環的最小偏置距離，利用式（4）求出的中間分支點及第一個無自交非凸多邊形環上的控制點，連接成新的非凸多邊形（圖16）。然后按3.3凸多邊形偏置算法的步驟對所有無自交凸多邊形環進行偏置操作直至無法再提取多邊形環為止。最后中軸提取方法提取凸多邊形的中軸（圖17）。

5.結果分析

從凸多邊形和非凸多邊形的偏置處理及中軸提取實驗結果來看，基于角平分線的無孔復雜多邊形中軸提取算法可以基本滿足多邊形的偏置及中軸提取的目的，同時可以減少自交檢測的復雜度。

6.結論

本文在現有草火模型及最大圓盤模型的基礎上，提出了一種基于角平分線的無孔復雜多邊形中軸提取算法。該算法利用多邊形凹凸點的偏置處理來獲得中間分支點，然后利用“手擠”邊界的方式獲得中軸，并利用邊界的連續拓撲結構保持中軸的連續性。實驗結果表明該算法能滿足中軸提取的要求并能保持中軸的連續性，而且減少了自交檢測的復雜程度。但目前該算法局限于無孔的復雜多邊形結構，尚未進行有孔多邊形驗證。下一步將進行有孔多邊形驗證及編寫程序驗證。

參考文獻

[1] 黎茂. 中軸變換研究[D]. 電子科技大學， 2006

[2] 徐春. 一種基于手的力反饋虛擬現實系統的研究[J]. 畢業生， 2003.

[3] 巴文蘭， 曹利新. 基于中軸變換的刀具優化選擇與刀具路徑規劃[J]. 大連理工大學學報， 2013（01）：63-68.

[4] Smogavec G， Zalik B. A fast algorithm for constructing approximate medial axis of polygons， using Steiner points [J]. Advances in Engineering Software， 2012， 52：p.1-9.

[5] Blum，H. A transformation for extracting new descriptors of shape [J]. Models for the Preception of Speech & Visual Form， 1967， 19：362-380.

[6] 呂哲， 王福利， 常玉清， et al. 改進的形態學骨架提取算法 [J]. 計算機工程， 2009， 035（019）：23-25.

[7] Arcelli， Carlo & Sanniti di Baja， Gabriella. （1985）. A Width- Independent Fast Thinning Algorithm. Pattern Analysis and Machine Intelligence， IEEE Transactions on.4. 463-474.

[8] 徐超， 肖瀟， 駱燕， 等. 基于距離變換的新型骨架提取方法 [J]. 儀器儀表學報， 2012（12）：213-218.

[9] Dey T K， Zhao W. Approximate medial axis as a Voronoi subcomplex[J]. Computer Aided Design， 2004， 36（2）：195-202.

[10] Yong， L.K. （2009）. 3D medial axis approximation through Delaunay triangulation. Journal of Science and Technology in the Tropics. 5. 133-139.

[11] 潘鵬， 賀三維， 吳艷蘭， 等. 曲邊多邊形中軸提取的新方法 [J]. 測繪學報， 2012， 041（002）：278-283，290.

[12] 王新生， 謝凱， 姜友華， 等. 復雜多邊形中軸構建方法 [J]. 武漢大學學報·信息科學版，2014，39：2， 2014， 39（2）：181-185.

[13] Liu L ， Chambers E W ， Letscher D ， et al. Extended grassfire transform on medial axes of 2D shapes[J]. Computer Aided Design， 2011， 43（11）：1496-1505.

[14] SONG Xiaomei， CHENG Changxiu， ZHOU Chenghu. An Analysis and Investigation of Algorithms for Identifying Convexity-Concavity of a Simple Polygon [J]. Remote Sensing for Land & Resources， 2011， 19（3）：25-31.

[15] 林福嚴， 鄭奇志， 胡于進， 周濟. 平面形體的中線提取及其應用[J].計算機應用與軟件 2000