基于雙向漸進結構優化方法的連續體結構動剛度拓撲優化

江旭東 劉錚 滕曉艷

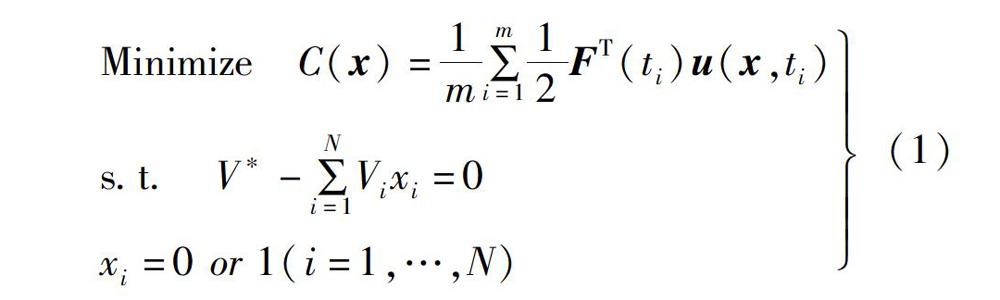
摘 要：以結構動柔順度最小為目標，融合等效靜載荷方法與雙向漸進結構優化方法，提出了動載荷作用下連續體結構的動剛度拓撲優化方法。為了有效降低結構動力學拓撲優化問題的求解規模，通過等效靜載荷方法將動態拓撲優化問題轉變為靜態拓撲優化問題，結合雙向漸進結構優化方法實現結構的靜力學拓撲優化。提出了一種設計域減縮方法降低連續體結構拓撲優化計算規模，構建了一種新穎的體積進化和優化收斂準則，顯著提高了連續體結構的動剛度優化效率。數值算例結果表明，結構動柔順度與約束體積均能漸進收斂于最優值，最優拓撲構形能夠有效抑制動載荷作用下的結構振動，其優化算法具有一定的魯棒性和適應性。提出的連續體結構動剛度拓撲優化方法拓展了基本漸進結構優化方法的應用范圍，對于結構動力學優化設計具有重要的理論意義。

關鍵詞：連續體結構;拓撲優化;動剛度;等效靜載荷;雙向漸進結構優化

DOI：10.15938/j.jhust.2020.05.019

中圖分類號： TB535.1

文獻標志碼： A

文章編號： 1007-2683（2020）05-0136-07

Abstract：By minimizing structural dynamic compliance， the programming scheme of optimal stiffness for continuum structure under dynamic load is proposed， by combination of Equivalent Static Loads with Bidirectional Evolutionary Structural Optimization. To effectively decrease calculation scale for dynamic optimization in structural topology， the Equivalent Static Loads Method is applied to transforming dynamic optimization to static one that is solved by Bidirectional Evolutionary Structural Optimization in structural topology. To enhance the optimal efficiency of the original BESO method to optimization of dynamic stiffness in continuum structure， a design domain reduction method is developed to establish a new volume control and a stop criterion in this study. Numerical results show that the dynamic compliance is asymptotically convergent to optimal solution with volume constraint precisely satisfied， and optimal configuration can effectively inhibit the vibration induced by dynamic load. Whereby the presented optimization algorithm is verified to be robust and adapt. Consequently it is provided with theoretical significance to extend the original Evolutionary Structural Optimization Method to dynamic optimization in structural design.

Keywords：continuum structure; topological optimization; dynamic stiffness; equivalent static loads; bidirectional evolutionary structural optimization

0 引 言

從拓撲層面上優化結構的動態響應特性，抑制結構振動及其機械噪聲的產生與傳遞，全面提高重大裝備技術水平，長期以來都是機械工程、力學以及優化理論等多學科領域關注的基礎性研究課題。近三十年來，形成了許多基于梯度或啟發式的拓撲優化方法，主要有均勻化方法（homogenization）、優化準則法（optimality criteria，OC）和SIMP方法（solid isotropic material with penalization）等優化數值求解方法[1-2]。其中，雙向漸進漸進結構優化（bidirectional evolutionary structural optimization，BESO）方法不僅能夠在高效區域添加單元，而且能夠在結構低效區域刪除單元，從而在漸進優化準則作用下形成最優的拓撲構型[3]。

目前，BESO方法在結構動態特性和動態響應優化方面已經取得了初步的研究進展。王磊等[4]以機床部件固有頻率為約束條件，提出了一種機床固定結合面形狀的拓撲設計方法。賀紅林等[5]以模態阻尼比最大化為優化目標，阻尼材料用量為約束，開展了粘彈阻尼抗振結構的低噪聲設計研究工作。Liu等[6]構建了復合材料結構宏觀-微觀雙尺度優化模型，研究了復合材料結構多尺度并行頻率優化方法。Picelli等[7]考慮了結構-聲的多場耦合作用，提出了聲振耦合結構的頻率優化方法。Vicente等[8]研究了流固耦合結構的頻率響應優化問題。近些年來，盡管BESO方法正在嘗試解決動態響應優化問題，但是動態優化的梯度計算代價太高，而且處理時域內的函數也相當復雜，直接開展動態響應優化設計往往由于計算規模大且很多時候難以收斂，而導致了其在工程應用中的不可行性[9]。

等效靜載荷法最早由Choi和Park針對動態線性優化問題而提出，它通過結構在動、靜態載荷作用下系統響應結果等效原理獲得等效靜態載荷，從而將結構動態響應優化問題轉化為結構靜態優化問題，為結構動態響應優化設計提供了有效的解決途徑[10]。Park等[11]，Stolpe等[12]證明了等效靜載荷法對于動態優化問題的最優解滿足Karush-Kuhn-Tucker 必要條件。與傳統的基于梯度的數值優化算法和啟發式全局優化算法相比，等效載荷法極大的降低了動力學優化問題的求解難度，顯著的提高了優化效率。目前，國內外研究學者已將等效靜載荷法應用于多體動力學系統的結構優化設計問題[13-14]，張艷崗等[15-16]從載荷等效轉化前后結構能量等效角度研究動態載荷等效靜態轉化問題，提出了一種基于關鍵時間點的能量等效靜態載荷法。

綜上，本文通過雙向漸進結構優化方法，以結構動柔順度最小化目標，構建連續體結構動剛度拓撲優化模型。將等效靜載荷方法與雙向漸進結構優化方法相融合，求解以動柔順度最小化為目標的結構動剛度優化問題。通過數值算例，驗證連續體結構動剛度拓撲優化方法的有效性。所提出的結構動力學優化方法將拓展雙向漸進結構優化方法的理論范疇，同時為工程結構動態響應優化設計提供一種新的思路。

1 結構動剛度拓撲優化

為了降低動載荷作用下的結構振動和機械噪聲的傳播，以結構動柔順度最小為目標，體積用量為約束條件，結合雙向漸進結構優化方法，結構動剛度拓撲優化模型表示為：

式中：C（x）為結構在動載荷F（ti）作用下的動柔順度;u（x，ti）為結構ti時刻的位移響應;m為F（ti）作用時間的均分數，x=[xi]N×1為結構優化設計變量;xi為第i個單元的相對密度;V、Vi分別為優化結構目標體積和單元體積。

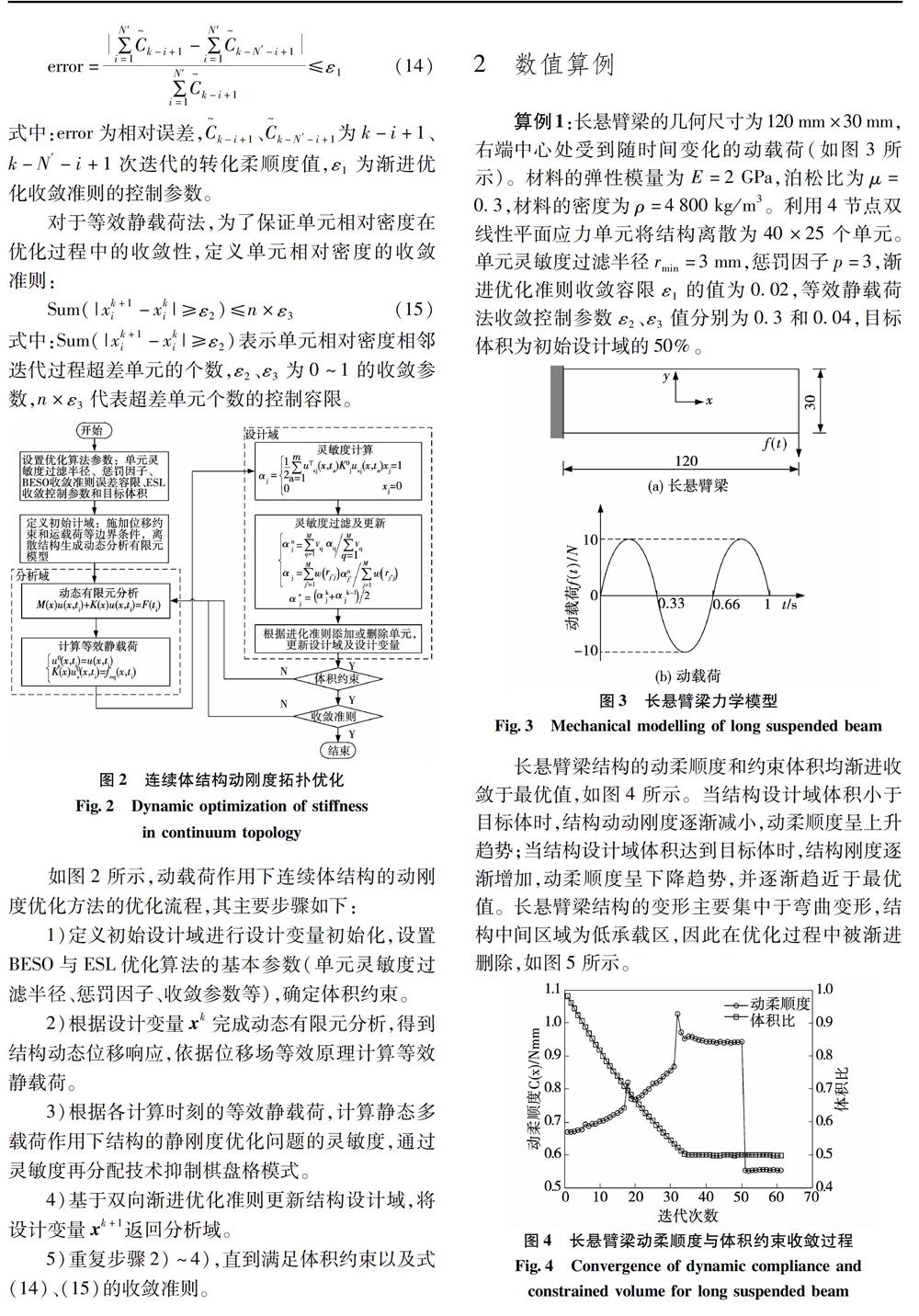
由式（1），動剛度優化的靈敏度分析涉及動態響應的梯度信息，需要求解大規模的動力學微分方程。由此，為了降低動力學優化計算規模，通過等效靜載荷法將將各離散時刻的動態載荷轉化靜態多工步載荷，從而將計算復雜的動態優化問題轉化為的靜態優化問題。如圖1所示，等效靜載荷法將結構動力學優化分為分析域和設計域：分析域求解結構動態位移場，基于位移場等效原理得到結構等效靜載荷;設計域依據雙向漸進結構優化準則更新結構設計域，同時將設計變量返回分析域實施動態響應分析。

4 結 論

為了有效抑制結構在動載荷作用下的機械振動，以結構動柔順度最小為優化目標，基于等效靜載荷方法和雙向漸進結構優化方法，提出了連續體結構的動剛度拓撲優化方法。

1）融合等效靜載荷方法和雙向漸進結構優化方法，將結構動剛度優化問題轉化為多工步載荷工況的線性靜剛度優化問題，利用雙向漸進結構優化方法實現了多工況線性靜力學優化，其優化算法具有一定的魯棒性和適應性。

2）提出了一種設計域減縮方法降低連續體結構拓撲優化計算規模，構建了一種新穎的體積進化和優化收斂準則，顯著提高了連續體結構的動剛度優化效率。

綜上，提出的連續體結構動剛度拓撲優化方法拓展了基本漸進結構優化方法的應用范圍，對于結構動力學優化設計具有重要的理論意義。

參 考 文 獻：

[1] SIGMUND O，MAUTE K. Topology Optimization Approaches [J]. Structural & Multidisciplinary Optimization， 2013， 48（6）： 1031.

[2] DEATON J. D，GRANDHI R. V. A Survey of Structural and Multidisciplinary Continuum Topology Optimization： Post 2000 [J]. Structural & Multidisciplinary Optimization， 2014， 49（1）： 1.

[3] MUNK D. J， VIO G. A， STEVEN G. P. Topology and Shape Optimization Methods Using Evolutionary Algorithms： a Review [J]. Structural & Multidisciplinary Optimization， 2015， 52（3）： 613.

[4] 王磊， 劉海濤， 金濤， 等. 一種機床固定結合面形狀拓撲設計方法[J]. 振動工程學報， 2014， 27（4）： 481.

WANG L， LIU J T， JIN T， et al. A Design Method of Fixed Joint Contact Area Topology-based Equivalent Model for Machine Tools[J]. Journal of Vibration and Engineering， 2014， 27（4）：481.

[5] 賀紅林， 陶潔， 劉堯弟， 等. 粘性阻尼抗振結構雙向漸進法拓撲動力學優化[J]. 農業機械學報， 2016， 47（8）： 339.

HE H L， TAO J， LIU Y D， et al. Dynamic Optimization of Damping Anti-vibration Structure Topology Based on BESO Method[J]. Transactions of The Chinese Society of Agriculture Machinery， 2016， 47（8）： 339.

[6] LIU Q M， CHAN R， HUANG X D. Concurrent Topology Optimization of Macrostructures and Material Microstructures for Natural Frequency [J]. Materials and Design， 2016， 106： 380.

[7] PICELLI R， VICENTE W M， PAVANELLO R， et al. Evolutionary Topology Optimization for Natural Frequency Maximization Problems Considering Acoustic-structure Interaction [J]. Finite Elements in Analysis and Design， 2015， 106： 56.

[8] VICENTE W M，PICELLI R， PAVANELLO R， et al. Topology Optimization of Frequency Responses of Fluid-structure Interaction Systems [J]. Finite Elements in Analysis and Design， 2015， 98： 1.

[9] TZARGLHAM S， WARD T A， RAMLI R， et al. Topology Optimization： a Review for Structural Designs under Vibration Problems [J]. Structural & Multidisciplinary Optimization， 2016， 53（6）： 1157.

[10]CHOI W. S， PARK G. J. Structural Optimization Using Equivalent Static Loads at All the Time InterVals [J]. Computer Methods in Applied Mechanics and Engineering， 2002， 191（19/20）： 2105.

[11]PARK G. J， KANG B.S. Validation of a Structural Optimization Algorithm Transforming Dynamic Loadsinto Equivalent Static Loads [J]. Theory Application， 2003， 118（1）： 191.

[12]STOLPE M. On the Equivalent Static Loads Approach for Dynamic Response Structural Optimization[J]. Structural & Multidisciplinary Optimization， 2014， 50（6）： 921.

[13]HONG E. P， YOU B. J， KIM C. H， et al. Optimization Flexible Components of Multibody Systems Via Squivalent Static Loads [J]. Structural & Multidisciplinary Optimization， 2010， 40（1）： 549.

[14]楊志軍. 基于等效靜態載荷原理的高速機構結構拓撲優化方法[J]. 機械工程學報， 2011， 47（17）： 119.

YANG Z J. Topological Optimization Approach for Structure Design of High Speed Mechanisms Using Equivalent Static Loads Method[J]. Journal of Mechanical Engineering， 2011， 47（17）： 119.

[15]張艷崗， 毛虎平， 蘇鐵熊， 等. 基于關鍵時間點的能量等效靜態載荷法及結構動態響應優化[J]. 機械工程學報， 2016， 52（9）： 151.

ZHANG Y G， MAO H P， SU T X， et al.Energy Equivalent Static Load Method Based on Critical Time Point and Structure Dynamic Response Optimization[J]. Journal of Mechanical Engineering， 2016， 52（9）： 151.

[16]張艷崗， 毛虎平， 蘇鐵熊， 等.基于能量原理的等效靜態載荷法及其在活塞動態優化中的應用[J]. 上海交通大學學報， 2015， 49（9）： 1293.

ZHANG Y G， MAO H P， SU T X， et al. Method of Equivalent Static Loads Based on Energy Principle and Its Application in Dynamic Optimization Design of Diesel Engine Piston[J]. Journal of Shanghai Jiao Tong University， 2015， 49（9）： 1293.

（編輯：王 萍）