橫向地震作用下異型鋼管混凝土拱橋地震易損性分析

王 力，虞廬松*，劉世忠，李子奇,2，劉 朋

(1. 蘭州交通大學 土木工程學院，蘭州 730070；2. 蘭州交通大學 甘肅省道路橋梁與地下工程重點實驗室，蘭州 730070；3. 中鐵上海設計院集團有限公司徐州設計院，江蘇 徐州 221000)

近30年來，世界上多次發生嚴重的震害，例如Northridge6.7級地震、Kobe7.2級地震、Chi-chi7.6級地震、汶川8.0級地震和東日本9.0級大地震等.強烈地震造成的災難性破壞給人民生命財產安全造成了創巨痛深的影響，同時也加速了震害預測和結構抗震理論等方面的發展.地震震害預測主要包括地震危險性分析、易損性分析、震害損失評估和可接受震害風險水平4個方面[1].橋梁結構作為交通要道的重要咽喉[2]，其在地震作用下若發生嚴重損傷甚至倒塌，可能會給抗震救災和災后重建工作帶來重大阻礙[3-4].進入新世紀以來，鋼管混凝土(concrete-filled steel tube,CFST)拱橋結構[5-6]以其造型優美、力學性能優越和施工方便等特點成為城市公路網中較為常見的橋型，因此，針對該類橋梁的地震易損性研究對減少地震直間接經濟損失及防止發生次生災害具有重要意義.

國外針對CFST結構的地震易損性研究主要集中于CFST橋墩等下部結構，對于CFST拱橋的地震易損性研究成果較少.在國內，謝開仲等[7]根據CFST拱橋各部件結構構造和受力特征，建立了考慮主要部件的雙重破壞評估模型，并基于模糊理論和層次分析法探究了CFST拱橋震害損傷和破壞情況.劉震[8]為探究中承式CFST拱橋的地震易損性，基于工程實際與統計資料對拱橋相關參數進行取值，根據雙重破壞準則判斷結構破壞狀態，通過概率分析得到了橋梁易損曲線及關于震級、震源距離的易損曲面.馮莉等[9]以PEER-PBEE理論為基礎，以一座高速鐵路CFST系桿拱橋為例，建立了橫向地震作用下的拱肋關鍵截面易損性曲線，并進行地震經濟風險分析.卓衛東等[10]以三跨中承式CFST系桿拱橋為例，基于增量動力分析(incremental dynamic analysis,IDA)計算結果，建立了橋梁關鍵部位的地震易損性曲線，得到盆式支座為該橋最易損構件.

目前，國內外對CFST拱橋地震易損性研究主要集中于常規CFST拱橋的構件地震易損性分析，而對異型CFST拱橋的相關研究較少.本文在已有研究基礎上，以一座異型CFST拱橋為例，建立其主要構件地震易損性曲線，并基于可靠度理論，探究結構整體地震易損性.

1 易損性分析流程

1.1 分析流程

地震易損性指結構在不同強度地震作用下發生某種損傷狀態的概率.該方法較傳統確定性方法能夠更全面地評估橋梁在地震作用下的遭到損傷的可能性.筆者以一座異型CFST拱橋為研究對象，建立全橋非線性有限元模型并進行非線性地震反應分析.選取主要易損構件為研究目標，繪制關鍵構件地震易損性曲線，最后，考慮構件之間的相關性，建立全橋系統地震易損性曲線.分析流程如圖1所示.

1.2 構件地震易損性

構件易損性分析中，用目標構件需求和其承載能力Sc來表示超越概率：

(1)

(2)

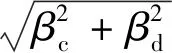
1.3 系統易損性

橋梁的延性性能指結構整體的延性，采用單一構件代替全橋系統的易損性可能會引起較大的誤差.異型CFST拱橋結構體系復雜，研究該類結構系統地震易損性時，須考慮各主要構件之間的耦聯效應.本文基于可靠度理論中的界限估計法，用系統失效概率的上、下界來表示該拱橋的系統地震易損性.

目前，常見的計算方法有一階界限估計(寬界限法)法和二階界限估計(窄界限法)法.一階界限估計法未考慮構件或失效模式之間的相關性，故相關系數ρ=0，表達式[1]如下：

(3)

式中：Pfi為橋梁結構單個構件的失效概率；Pf為橋梁系統失效概率.

采用一階界限估計法時，若將各個構件視為串聯關系，則單個構件失效概率的最大值即為橋梁系統失效概率的下限；若將各個構件視為并聯關系，則所有構件均失效的概率即為橋梁系統失效概率的上限.由于未考慮構件之間的相關性，因此給出的上下限區間較寬.

二階界限估計法是為著力解決一階界限估計法的缺點而提出的，該方法考慮了各個構件失效模式之間的相關性，其相關系數0<ρ<1，表達式[11]如下：

(4)

式中：Pf1表示某一構件的失效概率；Pfi表示除Pf1外其它構件的失效概率；Pfij表示兩個構件同時失效的概率.

2 工程概況與有限元建模

2.1 工程概況

以一座異型CFST系桿拱橋為研究對象.該橋主梁采用預應力混凝土分體式箱梁結構，梁寬29 m，梁長85.5 m，梁高2 m，在端部梁底局部加高至3 m，加高段長8 m.拱軸線為二次拋物線，矢跨比為1/4.4，矢高為18.9 m.拱肋采用啞鈴型截面，其中鋼管采用Q345鋼材，壁厚20 mm，管內灌注C55微膨脹混凝土.拱肋間設1道K撐和4道啞鈴型一字橫撐.系梁采用C55混凝土澆筑.拱肋間共設26對傾角為50.2°的斜置吊桿.主墩墩身采用變截面板式墩，用C45混凝土澆筑，承臺和樁基礎混凝土等級為C25.結構總體構造如圖2所示.

2.2 有限元模型

該橋的抗震設防烈度為Ⅶ度，地震動峰值加速度(PGA)為0.15 g，場地特征周期為0.45 s.運用MIDAS/Civil建立全橋非線性有限元模型，如圖3所示.

模型中CFST拱肋和橋墩采用纖維單元模擬，其中，拱肋鋼管和橋墩主筋采用雙折線模型模擬，拱肋核心混凝土和橋墩混凝土采用Kent-Park模型模擬.吊桿采用桁架單元模擬，橫撐和K撐采用聯合截面模擬，系梁采用線性梁單元模擬.運用m法模擬樁土相互作用，支座采用一般連接模擬.模型共1 447個節點，1 212個單元.

2.3 自振特性

自振特性分析是進行抗震計算的基礎.運用多重Ritz向量法對該橋進行自振特性分析，前5階振型特征如表1所列.

表1 自振特性Tab.1 Self-vibration characteristics

3 地震動選取與輸入

以算例橋梁所在場地設計反應譜為目標譜，從美國太平洋地震工程研究中心調用20條如圖4所示的實際地震記錄作為地震輸入.研究表明[12-13]，拱橋一般在豎橋向和縱橋向的抗震性能具有較好的安全儲備，而在橫橋向抗震問題較為突出.因此，本文主要分析背景橋例在橫向地震作用下的抗震性能.

4 損傷指標

在地震易損性分析中，一般將結構損傷狀態劃分為如表2所列的5個損傷等級.在損傷等級劃分時，構件損傷指標的選取通常對結構地震易損性結果影響較大.諸多橋梁抗震研究中，損傷主要發生在下部結構和支座系統，上部梁體和樁基礎發生破壞的案例較少[14]，CFST拱橋吊桿安全儲備也較充足.因此，本文參考既有研究和該橋主要構件的受力特點，以曲率延性比作為拱肋和橋墩損傷指標，以位移延性比作為支座損傷指標.

表2 拱橋構件損傷指標Tab.2 Damage index of arch bridge components

5 地震易損性分析

以0.1 g為步長對已選取的20條天然地震動從0～1.5 g進行等步長調幅，并輸入有限元模型進行IDA分析.

5.1 構件地震易損性

根據Cornell提出的冪運算定律，即：設地震作用下，結構響應與地震強度參數滿足對數線性關系[16-17].在此，提取拱肋、支座和橋墩的IDA分析結果，并通過式(1)進行對數化，再將對數化后的響應結果與ln(PGA)進行線性回歸分析.分析結果如表3所列.

將表3的計算結果代入式(2)即可求得支座、橋墩和拱腳在不同損傷狀態下的超越概率.最后，以PGA為自變量，構件各損傷狀態的超越概率為因變量，繪制得如圖5所示的異型CFST拱橋主要構件地震易損性曲線.

表3 主要構件地震需求響應回歸分析Tab.3 Seismic demand response regression analysis of main components

由圖5可得：各構件在地震荷載作用下對應各級損傷狀態的概率均隨著PGA的增大而增大；當PGA為0.15 g時，橋墩、支座和拱肋發生輕微損傷的概率為42.6%、36.3%和1.0%，可見該橋橋墩和支座為易損構件，而拱肋發生震損的概率較小；其它三種損傷狀態下，地震強度相同時，各構件損傷概率表現為支座>橋墩>拱肋.當E2強度地震作用(PGA=0.33 g)時，支座和橋墩發生中等損傷的概率均超過80%，發生嚴重損傷的概率分別為59.6%和40.3%，發生完全損傷的概率分別為38.6%和3.9%，而拱腳位置發生損傷的概率遠小于支座和橋墩.

從主要構件的地震易損性曲線可以快速獲取目標構件在不同強度地震作用下的損傷概率，可以指導拱橋抗震設計的局部優化.

5.2 系統地震易損性

目前，對橋梁構件之間相關系數的取值尚無統一定論，本文根據已有橋梁震害情況并參考文獻[18]，取橋墩與支座相關系數為0.1、拱肋和支座、橋墩的相關性為0.5.分別運用一階界限估計法(式3)和二階界限估計法(式4)對全橋系統易損性進行計算，繪制得系統易損性曲線如圖6所示.

由圖6可得，該異型CFST系桿拱橋系統地震易損性主要由支座和橋墩控制.采用一階界限估計法所得由輕微到完全損傷狀態的概率上下界最大帶寬分別為0.202、0.212、0.240和0.167，采用二階界限估計法所得的各損傷狀態最大帶寬分別為0.054、0.052、0.033和0.027.相較而言，二階界限法較一階界限法帶寬降低73.3%～86.3%，故二階界限估計法對系統易損性評估結果具有更高的準確度.

對比圖5和圖6可以發現，系統易損性比任意單個構件的易損性均要大，僅用單個構件易損性代替全橋系統易損性可能高估結構整體抗震性能.

6 結論

以一座公路異型CFST系桿拱橋為工程背景，分析了其在地震作用下的主要構件易損性和全橋系統易損性，得到如下結論：

1) 地震作用下，該異型CFST拱橋整體抗震性能較好，拱肋最易損區域位于坦拱拱腳位置，全橋最易損構件為支座和橋墩.

2) E2地震作用下，該異型CFST拱橋橋墩通過良好的延性來耗能，而支座位移響應較大，易引起橋梁損傷，在抗震設計中應予以重視.

3) 在輕微、中等、嚴重和完全損傷狀態下，二階界限估計法較一階界限估計法帶寬降低了73.3%～86.3%，大幅提高了該異型CFST拱橋系統地震易損性的計算精度.

基于二階界限估計法研究該橋系統易損性時，在構件相關系數的選擇上存在一定主觀性，如何尋求更客觀的方法計算確定各構件相關系數，是需要進一步研究的問題.