工業余熱回收儲備系統的經濟優化配置

王晉達， 周志剛， 劉 京， 趙加寧， 鄭進福、4

(1.哈爾濱工業大學建筑學院，黑龍江哈爾濱150006；2.哈爾濱工業大學寒地城鄉人居環境科學與技術工業和信息化部重點實驗室，黑龍江哈爾濱150006；3.河北工業大學能源與環境工程學院，天津300401；4.青島理工大學環境與市政工程學院，山東青島266033)

1 概述

工業余熱在我國北方供熱地區廣泛存在，但由于能量品位偏低(例如，熱電廠凝汽余熱的溫度只有20～30 ℃)且日內供應量分布受工藝生產過程嚴重制約，其總體利用率依然處于較低的水平[1]。另一方面，受制于經濟發展水平和能源資源條件，我國的集中供熱通常以煤炭作為主要能源，燃煤熱電機組和區域鍋爐房在供暖期的高負荷率運行造成了嚴重的空氣污染，因此加快推進清潔供熱的任務十分緊迫[2]。

在既有常規區域供熱系統的基礎上，新增合理容量的清潔供熱設備，能夠促進工業余熱的有效利用，顯著降低供熱系統的總運行費用，帶來可觀的經濟收益。

2 常規區域供熱系統的余熱回收儲備改造

圖1為常規區域供熱系統進行工業余熱回收儲備改造后的配置結構。由圖1可以看出，供熱系統的常規熱源包括熱電聯產機組、燃煤鍋爐和燃氣調峰鍋爐；余熱回收儲備系統則由余熱回收裝置(余熱鍋爐或低溫換熱器)、低溫蓄熱罐、蓄放熱水泵和電熱泵組成。關鍵外部條件包括工業余熱的實時供應狀況和區域電網的分時電價政策。總體上，余熱回收儲備系統與常規熱源并聯，共同承擔同一系統的供熱負荷。

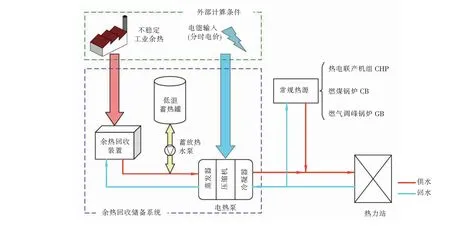
圖1 常規區域供熱系統進行工業余熱回收儲備改造后的配置結構

工業余熱的溫度通常較低(約10～40 ℃)，無法直接用于區域供熱，因此配置電熱泵提升工業余熱的能量品位，是實現余熱供熱利用的重要手段。另外，與地表水、空氣源熱泵相比，余熱回收儲備系統中電熱泵的蒸發溫度更高，制熱性能系數更大。為克服工業余熱不穩定供應所造成的負面影響，增強電熱泵的運行靈活性并獲得更大的余熱回收效益，改造方案同時還配置有低溫蓄熱罐和蓄放熱水泵。

3 改造系統的運行優化調度

區域供熱系統的運行優化調度本質上是通過制定系統所有產能單元的運行計劃(逐時啟停機狀態和制熱功率)，在滿足用戶熱負荷需求和全部相關設備調節能力約束的條件下，實現系統運行成本最小。

3.1 運行優化調度的目標函數

對圖1所示余熱回收儲備改造后的區域供熱系統，運行優化調度的目標函數為：

Φgb(t)Cgb+Φhp(t)Chp(t)

(1)

式中Π——區域供熱系統整個供暖期的總運行費用，元

Δτ——系統運行優化調度的調節周期，h，通常為1 h

N——供暖期供熱系統的總運行時間，h

Φchp(t)——t時刻熱電聯產機組的制熱功率，MW

Cchp——熱電聯產機組單位制熱量的運行費用，元/(MW·h)

Φcb(t)——t時刻燃煤鍋爐的制熱功率，MW

Ccb——燃煤鍋爐單位制熱量的運行費用，元/(MW·h)

Φgb(t)——t時刻燃氣調峰鍋爐的制熱功率，MW

Cgb——燃氣調峰鍋爐單位制熱量的運行費用，元/(MW·h)

Φhp(t)——t時刻電熱泵的制熱功率，MW

Chp(t)——t時刻電熱泵單位制熱量的運行費用，元/(MW·h)

Φhp(t)和Chp(t)可由下式計算得到：

(2)

式中Ihp——電熱泵的制熱性能系數

Php(t)——t時刻電熱泵的耗電功率，MW

Y(t)——t時刻區域電網的分時電價，元/(MW·h)

3.2 約束條件

區域供熱系統運行優化調度的約束條件分為系統約束和單元約束兩大類。

3.2.1 系統約束

改造后區域供熱系統的系統約束包括：一級管網熱平衡約束：熱源的總供熱量與熱負荷逐時相等；余熱回收儲備系統的能量平衡約束：逐時余熱回收量和低溫蓄熱罐釋放量之和應等于電熱泵的逐時余熱利用量；余熱資源量約束：逐時余熱回收量不能超過逐時可回收工業余熱量；一級管網供水溫度約束：當一級管網的設計供水溫度高于電熱泵的設計供水溫度時，為保證用戶末端的供熱質量，熱泵供熱量與常規熱源供熱量之間存在比例約束。在供暖期任意時刻(t=1,2，…,N)，區域供熱的系統約束見式(3)。

(3)

式中Φ(t)——t時刻區域供熱的總熱負荷，MW

Φhrb(t)——t時刻余熱回收裝置的制熱功率，MW

Φdsa(t)——t時刻低溫蓄熱罐的放熱功率(小于0代表罐體蓄熱)，MW

Φkhy(t)——t時刻區域供熱系統的可回收工業余熱量，MW

qm,hp(t)——t時刻進入電熱泵的一級管網循環質量流量，t/h

θhp,1——電熱泵冷凝器側的設計供水溫度，℃

qm,ths(t)——t時刻進入常規熱源的一級管網循環質量流量，t/h

θs,max——保證運行安全的一級管網最高輸送溫度，℃

θs(t)——t時刻一級管網的設計供水溫度，℃

3.2.2 單元約束

改造后區域供熱系統的單元約束包括：不同熱源的裝機容量及調節范圍約束；蓄熱設備總容量與水泵蓄、放熱能力約束。在優化調度周期內的任意時刻(t=1,2,…,N)，需滿足式(4)中的不等式約束條件。

(4)

式中Φz,chp——熱電聯產機組的裝機容量，MW

Φz，gb——燃氣調峰鍋爐的裝機容量，MW

Φz，hrb——余熱回收裝置的裝機容量，MW

Φp,max——蓄放熱水泵的最大蓄放熱能力，MW

Φcb,min——燃煤鍋爐的最小穩燃制熱功率，MW

Φz，cb——燃煤鍋爐的裝機容量，MW

Pz，hp——電熱泵的裝機容量，MW

Q(t)——t時刻低溫蓄熱罐的蓄熱量，MW·h

Qdsa——低溫蓄熱罐的總蓄熱容量，MW·h

Q(t)、Qdsa和Φp,max可由下式計算得到：

(5)

式中Q0——蓄熱罐的初始蓄熱量，MW·h

k1，k2——單位換算系數

ρ——低溫蓄熱罐中的熱媒密度，kg/m3

cp——低溫蓄熱罐中的熱媒的比定壓熱容，J/(kg·K)

Δθ——低溫蓄熱罐的蓄熱溫差，℃

Vdsa——低溫蓄熱罐的有效蓄熱容積，m3

qm,p——蓄放熱水泵的額定質量流量，t/h

3.3 決策變量

既有區域供熱系統在進行余熱回收儲備改造后，運行優化調度的決策變量出現變化，常規和新增決策變量見表1。需要指出，Φhrb(t)和Φdsa(t)并非改造后區域供熱系統運行優化調度的決策變量，而是約束條件內的中間變量。

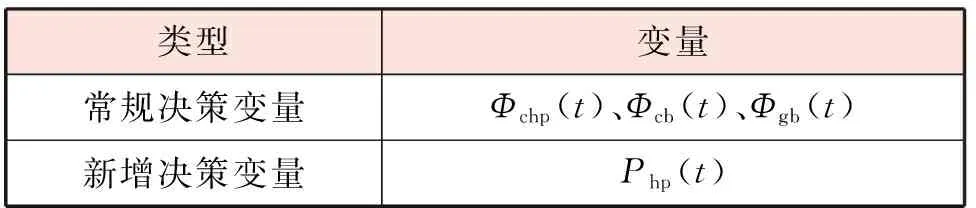
表1 改造系統運行優化調度的決策變量

解決本節所提出的供熱系統優化調度問題本質上是要求解高維線性規劃，目前已有很多的成熟算法工具箱可供選擇，本文后續案例采用MATLAB優化工具箱函數linprog進行具體解算。

4 余熱回收儲備設備的經濟優化配置

新增一定配置容量的余熱回收裝置、低溫蓄熱罐和蓄放熱水泵本質上是對既有供熱系統的改造，適合采用增量比較法進行工程經濟分析[3]。

4.1 新增設備優化配置的目標函數

既有區域供熱系統余熱回收儲備改造項目的經濟收益來源于系統更低的運行費用，代價則為新增設備的投資。對圖1所示的改造方案，優化配置問題所對應的目標函數為：

(KhpΦz,hp+KhrbΦz,hrb+KdsaVdsa+Kpumpqm,p)

(6)

式中Ψ——余熱回收改造項目的供暖期綜合收益，元

Πref——改造前區域供熱系統供暖期的基準總運行費用，元

Πnew——改造后區域供熱系統供暖期的總運行費用，元

i——經濟性分析的社會折現率

n——新增設備的預期使用壽命，a

Khp——電熱泵單位裝機容量投資，元/MW

Khrb——余熱回收裝置單位裝機容量投資，元/MW

Kdsa——低溫蓄熱罐單位有效容積投資，元/m3

Kpump——蓄放熱水泵單位額定質量流量的投資，元/(t·h-1)

Πref和Πnew的表達式如下：

(7)

式中g( )——表征區域供熱系統優化運行調度的隱函數

Ωref——區域供熱系統的常規熱源配置

Ωnew——余熱回收儲備系統的配置組合

結合式(6)～(7)可以看出，余熱回收儲備改造項目的供暖期綜合收益僅由新增設備的配置組合(Ωnew)決定。

4.2 決策變量的顯式約束

為正常啟動優化計算，需對每個決策變量設定一個最大的搜索上界，改造項目經濟優化配置的約束條件為：

(8)

式中Φmax,hp——新增電熱泵裝機容量的搜索上界，MW

Φmax,hrb——新增余熱回收裝置裝機容量的搜索上界，MW

Vmax,dsa——新增低溫蓄熱罐有效容積的搜索上界，m3

qm,pump——新增蓄放熱水泵額定質量流量的搜索上界，t/h

4.3 優化計算流程與求解算法

獲得余熱回收儲備系統新增設備最優配置容量的總體計算流程由內、外兩層優化模型嵌套而成(稱為雙層優化配置模型)。內層優化是在特定的系統配置組合、外部條件(包括電網分時電價、系統逐時熱負荷與可用余熱資源)和技術經濟參數(各設備投資費用參數、等額回收系數等)取值下，所進行的區域供熱系統的常規運行優化調度，最終能夠得到某配置組合所對應的供暖期總運行費用。外層優化則是對余熱回收儲備系統新增設備的最優容量組合進行全局搜索，在此過程中需重復調用內層的優化計算模塊。

在外層優化計算中，由于目標函數無法由決策變量顯式表達，因此基于梯度或高階導數信息的常規優化算法對該問題并不適用。

作為進化算法的重要分支，遺傳算法提供了一種通用的優化求解框架，能夠有效處理決策變量較多、目標函數高度非線性的優化問題[4]。此外，直接搜索也是解決優化配置問題的可行途徑，作為典型的直接搜索算法，模式搜索無需任何有關目標函數梯度的信息，對某些復雜黑箱問題的優化效果很好[5]。

本文利用MATLAB的優化工具箱函數ga和pattersearch對新增余熱回收儲備系統設備優化配置問題進行定量優化計算，并采用工具箱的默認設置。編程計算的重點在于適應度函數句柄(@objectfun)的構造，這需要根據供熱系統的特定狀況專門編寫。

5 案例計算與分析

5.1 計算條件

5.1.1 系統逐時熱負荷及可回收余熱資源

測試區域供熱系統的逐時熱負荷及可回收余熱負荷分別見圖2、3。從圖2可以看到，供熱系統的逐時熱負荷同時存在較為顯著的日內波動和季節性變化，嚴寒期的最大熱負荷(695 MW)約為供熱初末期最小熱負荷(105 MW)的7倍。

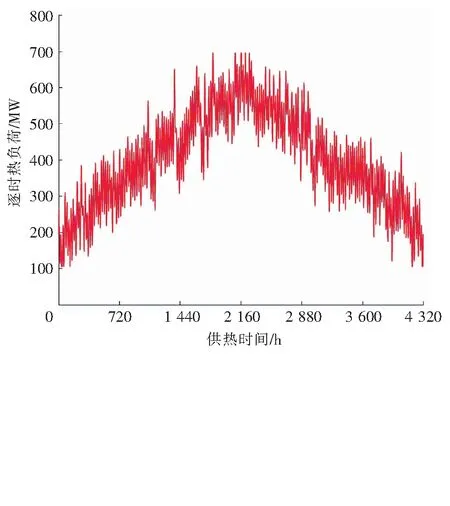
圖2 測試區域供熱系統的逐時熱負荷

圖3為0～72 h區域供熱系統的逐時可回收工業余熱負荷曲線，可以看出可回收工業余熱負荷呈現明顯的日周期變化規律(波動變化模式與工藝生產過程密切相關)，每天可回收工業余熱的總量相差不大。

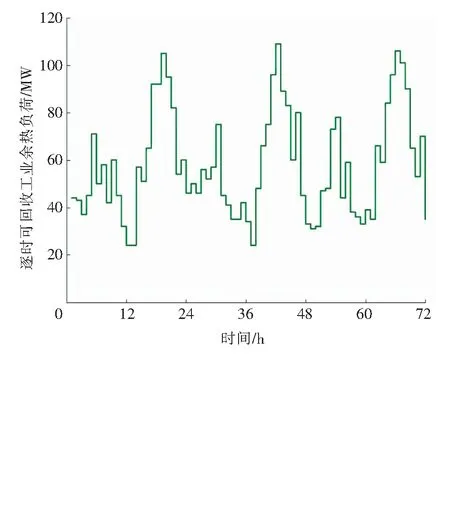
圖3 測試區域供熱系統的逐時可回收工業余熱負荷

5.1.2 常規熱源配置與供熱成本

測試區域供熱系統常規熱源的配置、供熱成本及調度優先級見表2。不同類型熱源的供熱成本有很大差異，燃氣調峰鍋爐的供熱成本甚至為熱電聯產機組的6倍。在供熱系統的運行優化調度中，熱源的供熱成本越低，調度優先級就越高。隨著系統熱負荷的不斷增加，只有當調度優先級較高的機組滿負荷運行仍不能滿足供熱需求時，才開啟調度優先級較低的機組。

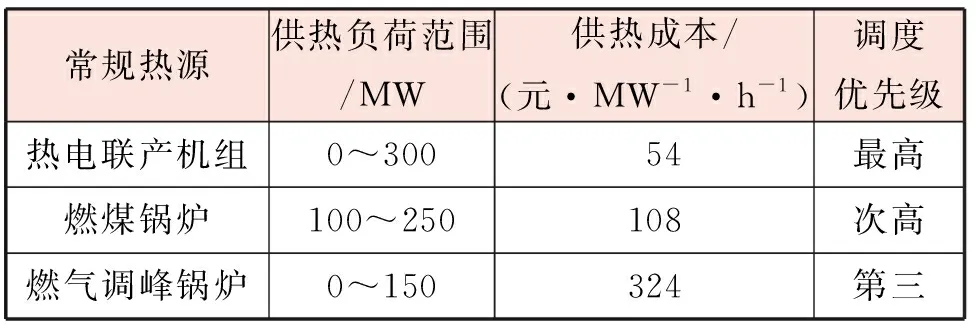
表2 常規熱源的配置、供熱成本及調度優先級

5.1.3 經濟、技術參數的取值

余熱回收儲備系統的經濟優化配置需基于確定的技術、經濟參數。本案例計算的相關參數見表3，其中Khp,Khrb,Kdsa和Kpump根據已有的相似工程案例折算得到[6]；假設電熱泵的供水溫度θhp,1和回水溫度θhp,2在整個供暖期保持恒定(即制熱性能系數Ihp為定值)。表3中ηhp為電熱泵的等效機械效率,θz為蒸發器、冷凝器內的換熱溫差，單位為℃。

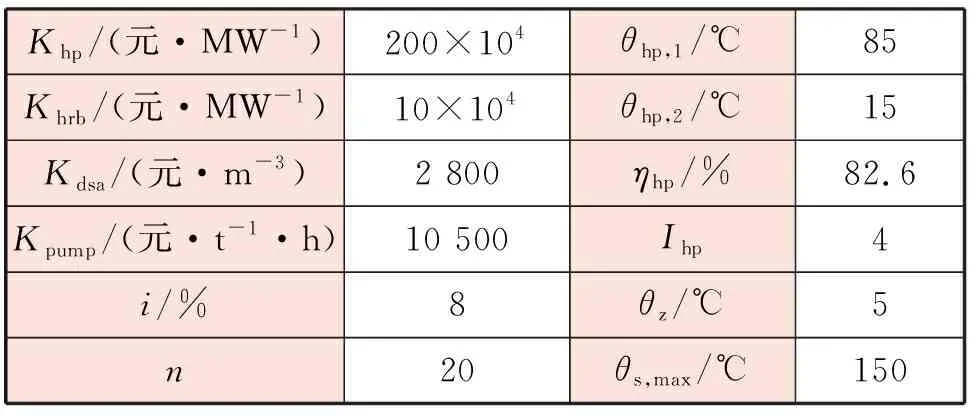
表3 案例計算的相關技術經濟參數

5.1.4 分時電價

測試案例區域電網的分時電價見表4。在熱泵制熱性能系數已知且恒定的條件下，調用式(2)可得到新增電熱泵不同時段的供熱成本，見表4。

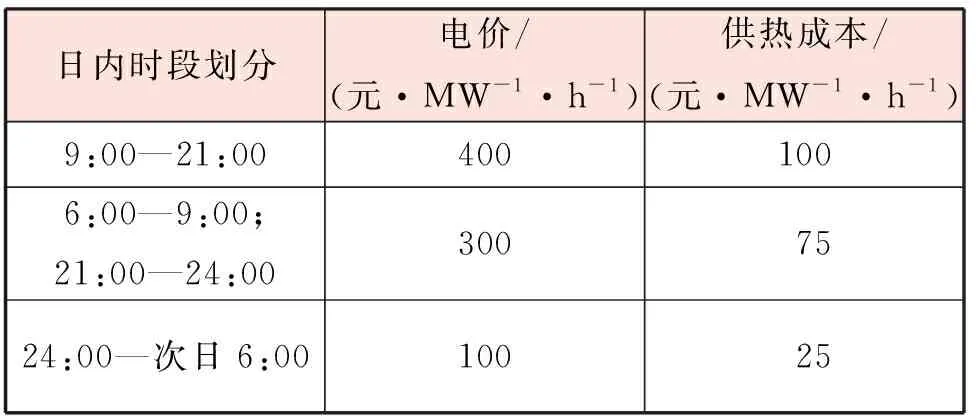
表4 分時電價與新增熱泵的供熱成本

在谷價電時段，新增電熱泵的供熱成本為25元/(MW·h)，低于熱電聯產機組的供熱成本，因此具有最高調度優先級；而在平價、峰價電時段，電熱泵的供熱成本在熱電聯產機組和燃煤鍋爐之間，其調度優先級僅低于熱電聯產機組。

5.2 不同優化算法的效能比較

在默認的算法選項設置下，分別調用MATLAB遺傳算法和模式搜索優化工具對余熱回收儲備系統的優化配置問題進行多次獨立計算，結果見表5～7。

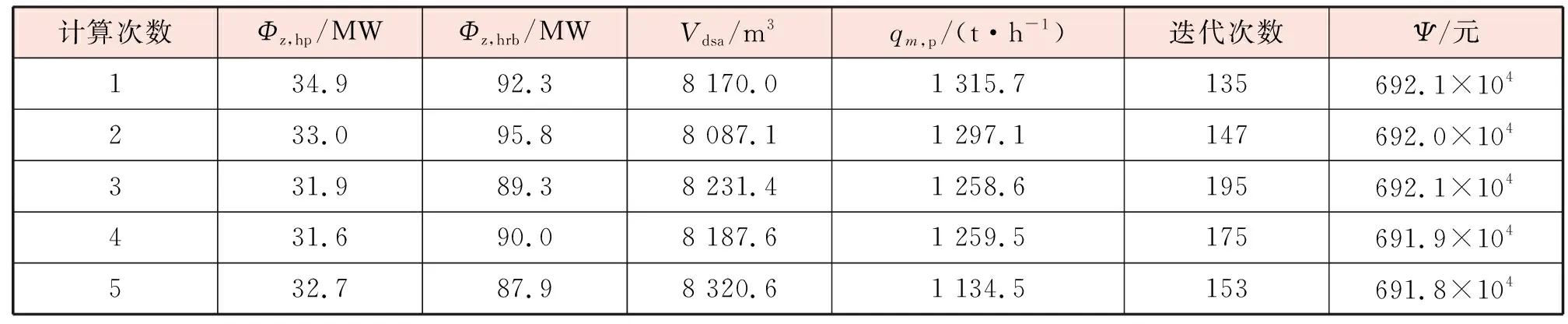
表5 多次獨立遺傳算法優化的計算結果

表6 遺傳算法決策變量的標準差和變異系數

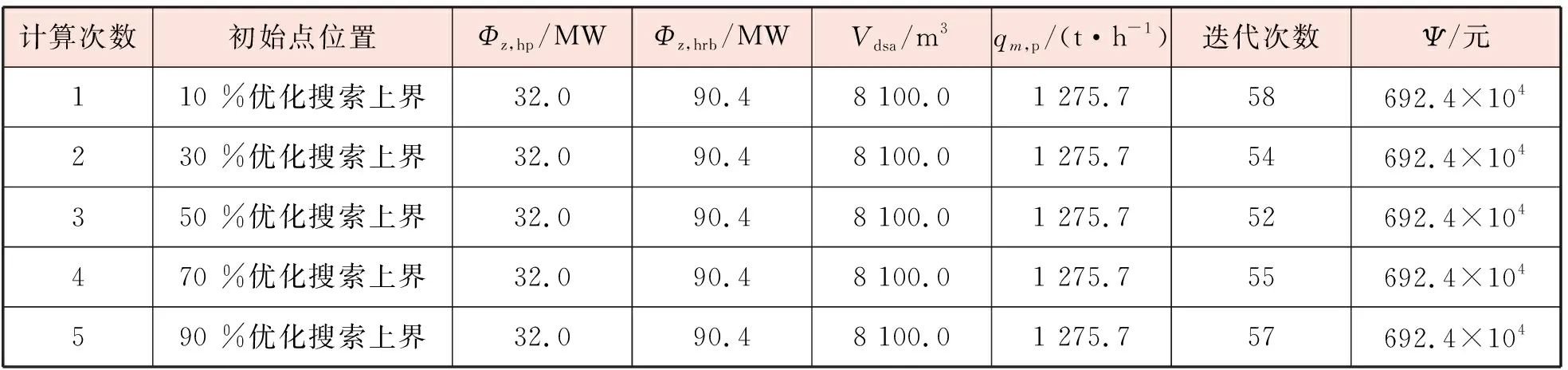
表7 不同初始點模式搜索的優化計算結果

結合表5～7可以看出：①遺傳算法達到收斂的迭代次數為模式搜索的2倍以上(甚至可達4倍)；另外在遺傳算法中，種群進化需要計算全部個體的適應度，因此在默認算法設置下(種群數量50、模式搜索網格點數目為8)，遺傳算法的計算負荷在模式搜索的12.5倍以上。②遺傳算法在求解本案例優化配置問題時計算穩定性差、易陷入局部最優(因為表征優化計算穩定性的決策變量標準差及變異系數均大于0)；與遺傳算法相比，模式搜索對初始點的位置不敏感，最終都能夠有效地收斂到同一點，且收斂迭代次數接近。③基于模式搜索得到的供暖期綜合收益比5次獨立遺傳算法優化的結果更好，因此可認為表7的優化計算結果是余熱回收儲備系統的最優配置。

5.3 余熱回收儲備改造的總體效果

表8為1個供暖期余熱回收儲備改造前、后系統各熱源的總供熱量和運行費用。可以看到燃煤鍋爐、燃氣調峰鍋爐的總供熱量和運行費用均有顯著降低，整個供暖期的總運行費用從13 093.2×104元降低到11 292.5×104元，降幅達13.8 %。

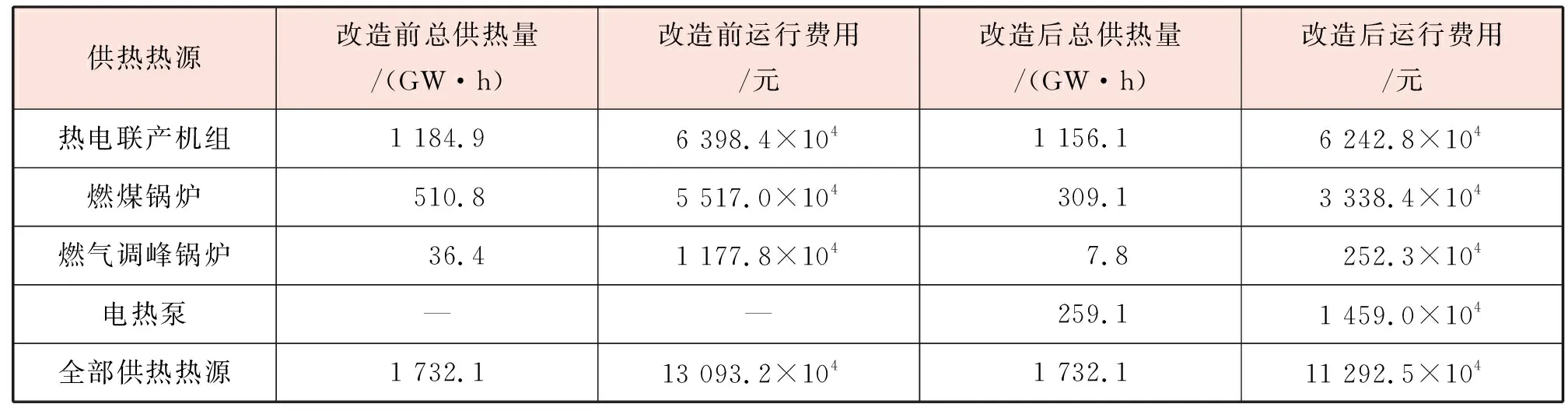
表8 1個供暖期余熱回收儲備改造前、后系統各熱源的總供熱量與運行費用

6結論

對既有區域供熱系統清潔改造的經濟優化配置問題進行深入研究，給出利用低價電能促進工業余熱回收利用的系統改造方案。對改造系統的運行優化調度進行分析，基于增量比較法提出余熱回收儲備設備的雙層優化配置模型。基于案例計算對提出的經濟優化配置模型進行驗證，結果表明：相比遺傳算法，模式搜索在求解雙層優化配置模型時，具有更快的收斂速度和更高的計算穩定性；合理配置余熱回收儲備設備能夠獲得可觀的供暖期綜合收益。