碳纖維-鋼復合結構不同粘結界面對ΔKII影響的仿真研究*

李 璐，王斌華，黃遲航

(長安大學道路施工技術與裝備教育部重點實驗室，陜西 西安 710064)

0 引 言

復合材料已成為與金屬材料、無機非金屬材料、高分子材料并列的四大材料體系之一[1]。碳纖維增強聚合物(Carbon Fiber Reinforced Polymer，CFRP)的比強度和比剛度高，加固過程不會增加鋼梁自重，不對鋼梁產生破壞，已經廣泛應用在鋼材加固補強中[2]；尤其是外貼CFRP片材的加固技術在工程加固領域中應用逐漸增多，CFRP的外部粘結可以在很大程度上延長結構疲勞壽命并減緩裂紋擴展[3-4]。

在CFRP-H型鋼復合結構中，較為薄弱的環(huán)節(jié)是粘結層界面，而復合結構的力學性能與粘結層的應力狀態(tài)密切相關；因此，提升復合結構的粘結層強度尤為重要[5]。由于粘結層很薄，采用傳統(tǒng)的有限元方法易造成計算收斂困難的問題；為解決此問題，基于黏聚區(qū)的模型(cohesive zone model，CZM)模擬粘結層，被廣泛應用于模擬復合材料結構的層間失效[6]。對于單一斷裂模式的雙懸臂梁(DCB)和端部缺口彎曲(ENF)試件中的裂紋擴展，國內外學者進行了廣泛研究，鄧健[7]指出當裂紋長度未超過試件半長時，由線彈性理論和小變形假設，可認為是單一模式下的斷裂類型。

但不同粘結層界面對復合結構強度的增強機理尚不明確，筆者采用雙線型本構模型，根據(jù)試驗數(shù)據(jù)[5]對材料屬性進行設置，利用Abaqus軟件分別模擬了三種(刻槽/Kevlar、刻槽/Kevlar/多壁碳納米管(MWCNT)和噴砂/MWCNT)粘結界面，建立CFRP-H型鋼復合結構的有限元模型，分別施加豎直向下不同大小的位移載荷，仿真得到復合結構應力強度因子幅ΔKII與Y向位移曲線，分析得到不同粘結界面的數(shù)值結果，并與理論結果進行對比，驗證數(shù)值模型的正確性。

1 本構模型及有限元模型參數(shù)設定

表1 不同試件的參數(shù)試驗值[5]

圖1 雙線型本構關系模型

2 建立有限元模型

2.1 材料屬性和模型尺寸

CFRP-H型鋼復合結構，包括H型鋼、粘結層和碳纖維布三種宏觀結構。假定粘結界面分別與H型鋼表面及CFRP粘結界面良好，在Abaqus軟件中基于CZM，采用cohesive單元(響應為牽引分離)模擬粘結層，模擬多相界面內部結構的粘彈性變形；模型材料屬性如表2所列，模型的幾何特征尺寸如圖2所示。

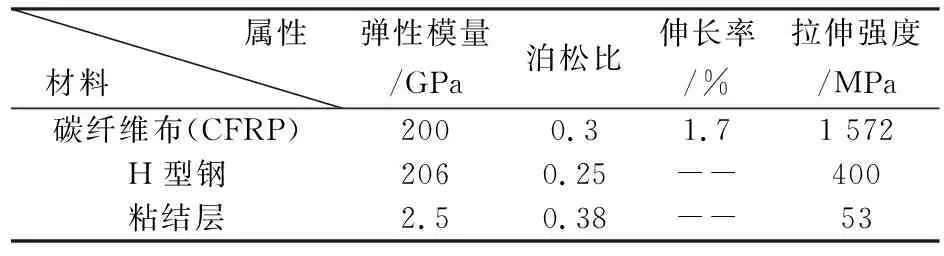
表2 模型的材料屬性

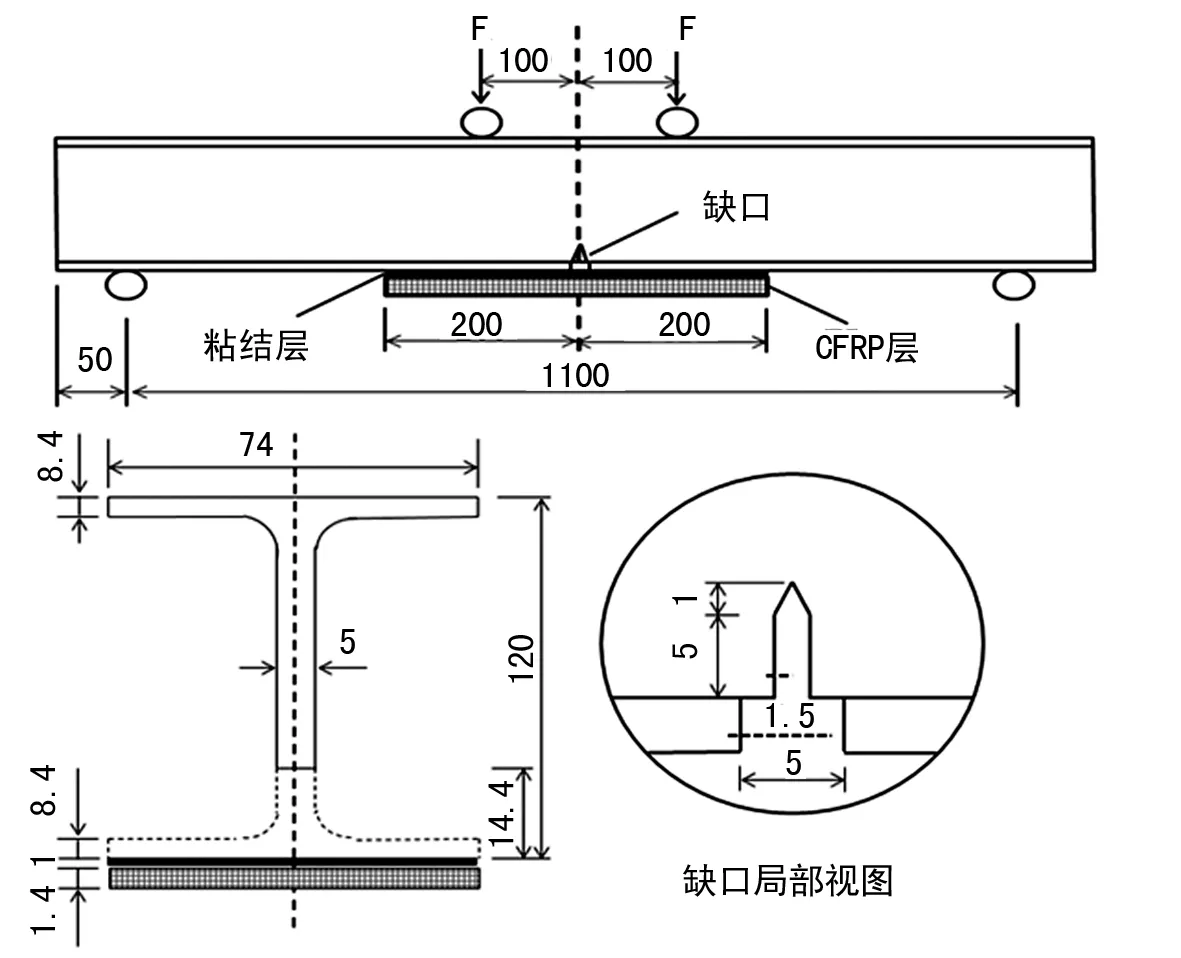
圖2 有限元模型的幾何特征尺寸(mm)

2.2 網格劃分

在CFRP-H型鋼復合結構的有限元模型中，單元共109 300個，節(jié)點159 981個。模型網格劃分如圖3所示：H型鋼采用線性縮減積分八節(jié)點線性六面體單元(C3D8R)模擬，在其預置缺口附近采用SWEEP劃分網格，且裂紋擴展方向為缺口尖端背離缺口中心；粘結層采用八節(jié)點三維粘結單元(COH3D8)模擬；碳纖維層采用C3D8R模擬。邊界條件是約束支撐1的三個移動自由度、支撐2的X和Y向移動自由度，規(guī)定豎直向下為Y的正向，負載施加Y正向的均勻位移載荷；鋼/粘結層和粘結層/CFRP界面使用TIE進行粘合。

圖3 有限元模型的網格劃分

2.3 計算結果與分析

選取粘接界面為噴砂/MWCNT的有限元模型，對粘結層的失效過程進行闡述，分析粘接界面對ΔKII的影響。規(guī)定豎直向下為Y的正向，不同Y向位移載荷的粘結層應力分布如圖4所示。

如圖4所示，分別對粘結層失效前見圖4(a)、(b)、失效中見圖4(c)、失效后見圖4(d)、(e)期的法向應力(S33)和剪應力(S13)進行分析。對失效前期，從圖4(a)可以看出，當位移載荷為2 mm時，載荷值為1 382 N，法向應力和剪應力集中在預置缺口附近，即位于粘結層前端18 mm的范圍內，此時粘結層沒有發(fā)生破壞，但粘結層前端的應力值較大，有發(fā)生破壞的趨勢；由圖4(b)可以看出，當位移載荷為4 mm時，載荷值為2 693 N，正向法向應力向兩邊移動了10 mm，負向法向應力集中在粘結層前端與CFRP接觸中部位置，而法向應力值整體相較圖4(a)有所減小，因為復合結構主要由剪應力承受外界施加的載荷，此時剪應力移動到粘結層后端的邊緣位置，此狀態(tài)下粘結層仍未出現(xiàn)失效。

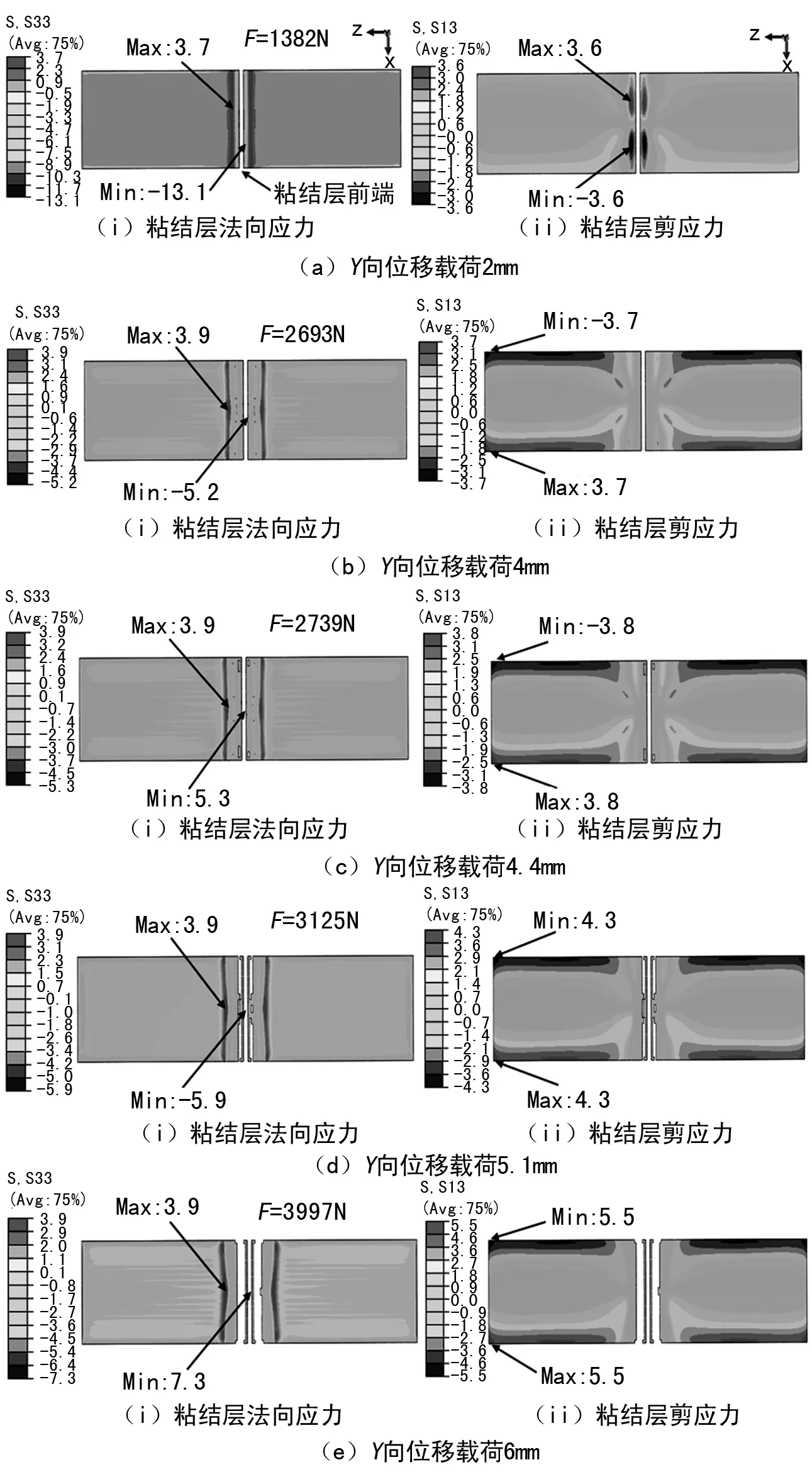
圖4 不同Y向位移載荷的粘結層應力分布(單位：MPa)

對失效中期，從圖4(c)看出，當位移載荷為4.4 mm時，載荷值為2 739 N，粘結層前端第二列單元格開始退化，退化位置距粘結層前端4 mm；相較圖4(b)，法向應力未發(fā)生改變，而剪應力值整體略有增加。由此可以認為粘結層的失效主要受剪應力的影響，當剪應力達到材料的極限值時，材料該部分就會退化失效。

對失效后期，從圖4(d)看出，當位移載荷為5.1 mm時，載荷值為3 125 N，粘結層前端第一列單元格保留，退化方向為粘結層前端指向后端，失效長度(單側粘結層)為6 mm，剪應力值整體略有增加，其余均未變化；從圖4(e)看出，當位移載荷為6 mm時，載荷值為3 997 N，此時總失效長度(單側)為11.9 mm，此時剪應力值達到最大，相較與圖4(a)，正向剪應力值提高了1.53倍。

由以上分析可知，法向應力對粘結層的影響較小，剪應力對粘結層失效起主導作用；當剪應力達到材料的剪切強度時，材料就開始退化，從而導致復合結構的失效。MWCNT和Kevlar的增韌使得粘結層的強度提升，CFRP分擔了更多的載荷，從而使得復合結構整體強度提升，ΔKII值減小。由于H型鋼和粘結層接觸區(qū)域受力較為集中，剪應力對粘結層有較大的影響，當剪應力達到其剪切強度時，粘結層就開始退化，裂紋擴展。仿真結果與理論結果一致，證明了模型的準確性。

對于不同的有限元模型(粘結層參數(shù)不同，其余均相同)，分別施加相同的Y向位移載荷，得到缺口附近應力強度因子幅ΔKII和Y向位移曲線，如圖5所示，隨著Y向位移的增加，ΔKII也逐漸增加；對于相同位移載荷作用下模型的ΔKII值，ΔKII未加固>ΔKII刻槽/Kevlar>ΔKII噴砂/MWCNT>ΔKII刻槽/Kevlar/MWCNT，表明刻槽/Kevlar/MWCNT界面增強效果最明顯，可顯著降低ΔKII值。

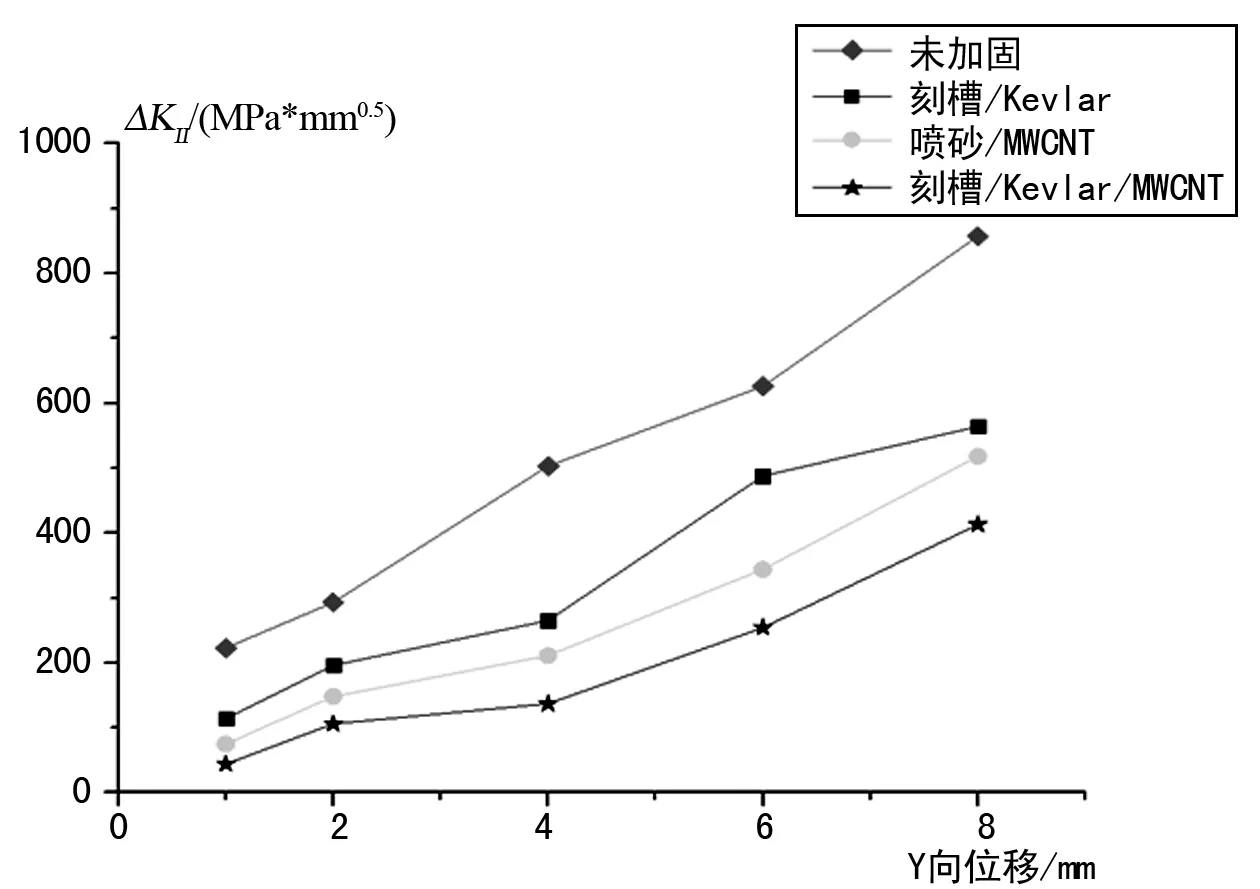
圖5 應力強度因子幅ΔKII與Y向位移曲線

3 結 論

以Abaqus有限元軟件為平臺，采用CZM模型模擬粘結層，分別模擬了三種粘結界面(刻槽/Kevlar、刻槽/Kevlar/MWCNT和噴砂/MWCNT)，建立了CFRP-H型鋼復合結構的有限元模型，施加不同的Y向位移載荷后，計算得到缺口尖端的ΔKII值，仿真結果與理論結果吻合較好，得出以下結論：

(1) 對于CFRP-鋼復合結構模型，各粘結界面應力值變化范圍較小，說明粘結層內部產生相互作用的內力越小，CFRP承擔了更多的載荷。

(2) 在粘結層中加入MWCNT和Kevlar可以顯著提高粘結層的剪切強度，有效降低缺口處ΔKII值。由實際情況可知：Kevlar短纖維的自由端可以隨機嵌入到金屬表面的槽中和CFRP布表面縫隙中，增強復合結構強度。

(3) 該模型模擬的CFRP層數(shù)和粘結層厚度為定值，為得到最優(yōu)的CFRP層數(shù)和粘結層厚度，仍需深入研究。