六旋翼動力學建模及PID定點懸停控制仿真*

申 旺,鄒樹梁,鄧 騫

(1.南華大學 機械工程學院，湖南 衡陽 421001； 2.南華大學 核設施應急安全作業技術與裝備湖南省重點實驗室 湖南 衡陽 421001)

0 引 言

近年來，多旋翼無人機因為其機動性、可靠性等優點成為研究熱點，而六旋翼無人機，相較于四旋翼無人機，具有更強的負載能力和更高的可靠性，而且由于其具有冗余的執行機構，可以在一個電機停止的情況時繼續工作。六旋翼無人機通過改變電機的轉速實現位置和姿態的控制，而六旋翼本身是一個欠驅動系統，進行對六旋翼的研究，特別是控制器的研究具有重大的意義。

國內外有許多學者進行了相關研究。徐會麗[1]采用改進的PIDNN算法對六旋翼進行控制，加快了響應速度，緩解了超調現象，并且減少了調參次數；黃佳奇[2]設計了一種基于反步法的控制器，實驗結果表明對無人機的位姿控制，所設計的控制器對定點懸停展現出良好的控制性能；王巍[3]利用滑模控制方法研究了四旋翼和三旋翼無人機的姿態調節和方位跟蹤的控制問題; 曾振華等[4]采用模糊自適應速度PID控制系統實現多旋翼的自主精準降落。

筆者基于牛頓-歐拉方程和牛頓第二定律，建立了六旋翼無人機的動力學模型，在小角度的假設條件下，對動力學模型進行了線性化處理，設計雙環PID控制器，在MATLAB/Simulink中搭建模型并實現定點懸停的仿真，驗證了模型的有效性，對后續控制系統的實驗具有參考意義。

1 六旋翼無人機概述

1.1 六旋翼無人機結構

無人機(Unmanned Aerial Vehicle,UAV),是利用無線電遙控設備和自備的程序控制裝置操縱的不載人飛機，六旋翼無人機則指旋翼數為6的無人機。根據旋翼的分布方式，分為I型，V型等，如圖1所示。

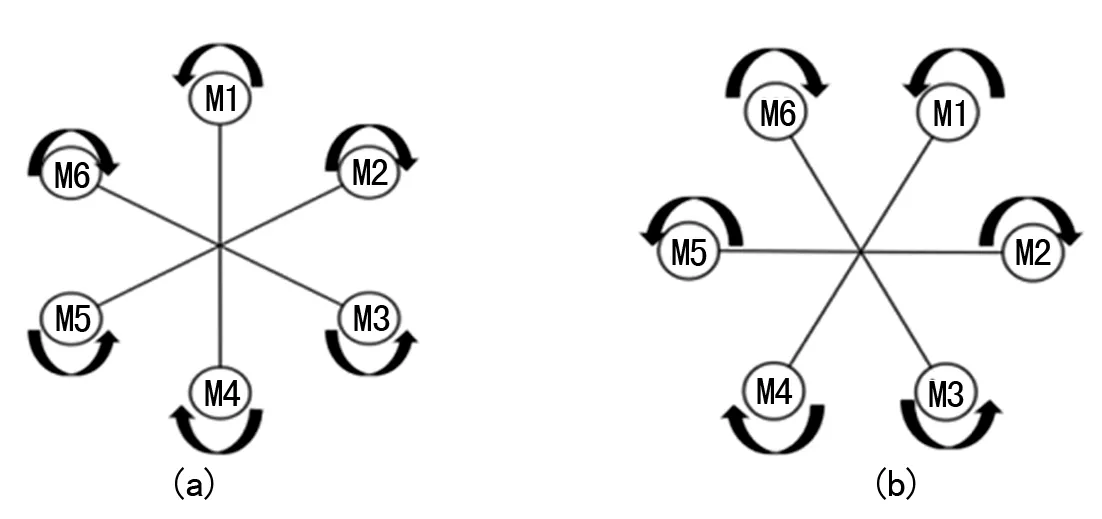
圖1 六旋翼無人結構

六旋翼無人機的機體由機架和旋翼組成。機架承載六旋翼所有組件，六旋翼的安全性、可用性都和機架的布局密切相關。旋翼隨電機轉動為無人機提供升力，相鄰兩旋翼的旋轉方向相反，反扭距可被有效抵消。與四旋翼無人機相比，六旋翼無人機具備冗余的執行機構，當遇到較強外力干擾或者部分旋翼受擾時能表現出更好的穩定性。

1.2 六旋翼飛行控制原理

以圖1(b)為例，說明四種基本運動的原理。

(1) 俯仰運動：規定機體抬頭為正，機體低頭為負。當無人機接收到抬頭指令時，1號、6號電機轉速增大，3號、4號電機轉速減小，產生使機體抬頭的力矩；收到低頭指令時，3號、4號電機轉速增大，1號、6號電機轉速減小，產生使機體低頭的力矩。

(2) 滾轉運動：規定向右滾轉為正，向左滾轉為負。當無人機接收到右滾轉指令時，4號、5號、6號電機轉速增大，同時1號、2號、3號電機轉速減小，產生使機體右滾轉的力矩；收到左滾轉指令時，1號、2號、3號電機轉速增大，4號、5號、6號電機轉速減小，產生使機體向左滾轉的力矩。

(3) 航運動：規定向右偏航為正，向左偏航為負。當無人機接收到右偏航指令時，1號、3號、5號電機轉速增大，2號、4號、6號電機轉速減小，產生使機體右偏航的力矩；當接收到左偏航指令時，2號、4號、6號電機轉速增大，1號、3號、5號電機轉速減小，產生使機體左偏航的力矩。

(4) 升降運動：規定上升為正，下降為負。當無人機接收到上升指令時，所有電機轉速增大，當升力大于重力時，無人機上升；當無人機接收到下降指令時，所有電機轉速減小，升力小于重力，無人機下降。

2 六旋翼動力學建模

2.1 建模假設條件

(1) 六旋翼是剛體；

(2) 六旋翼的質量和轉動慣量不變；

(3) 六旋翼的幾何中心和重心一致；

(4) 六旋翼只受重力和旋翼拉力，其中旋翼拉力沿zb軸向下，重力沿ze方向；

(5) 奇數標號的旋翼槳葉逆時針轉動，偶數符號的旋翼槳葉順時針轉動[5]。

2.2 旋轉矩陣的形成

地球坐標系e按照zyx順序旋轉到地球坐標系b，3次旋轉分別對應一個基本旋轉矩陣：

第1次為地球坐標系繞z軸旋轉ψ，得b1坐標系，對應基本旋轉矩陣為：

(1)

第2次為b1坐標系繞其y軸旋轉θ，得b2坐標系，對應基本旋轉矩陣為：

(2)

第3次為b2坐標系繞其x軸旋轉φ，得到b坐標系，對應基本旋轉矩陣為：

(3)

(4)

2.3 運動學模型

(5)

式中：ev為六旋翼在地球系下的速度矢量；Θ為姿態角；bw為機體角速度。

2.4 位置動力學模型

設旋翼轉速為Ωi(i=1,2,…6),產生的拉力為Ti，其關系如下[9]：

(6)

式中：Kt為拉力系數。

(7)

(8)

由牛頓第二定律，對六旋翼進行受力分析，在速度較小的情況下忽略阻力，可得:

mev·=eT-G

(9)

式中：G為重力。展開可得:

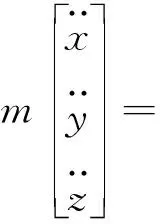
(10)

整理得:

(11)

2.5 姿態動力學模型

在機體坐標系下建立六旋翼姿態動力學方程如下:

Ibw·=-bw×(Ibw)+τ+Ga

(12)

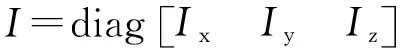
由文獻[7]可知：

(13)

其中，如圖2所示:l1=l2=l3=l4=l5=l6=l為機體中心到電機的距離，αi(i=1,2…5,6)表示機臂與xb軸正方向之間的夾角，Km為反扭距系數，則反扭距大小表示為：

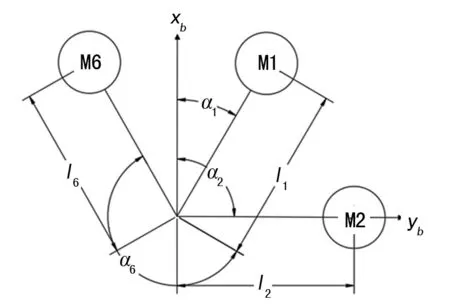
圖2 六旋翼機架布局參數

(14)

采用小角度假設，W≈I3，可以得到以下關系：

(15)

將式(13)～(15)代入式(12)展開可得：

(16)

2.6 模型線性化

六旋翼的動力學模型已經建立，為了方便控制器的設計，對非線性模型進行簡化和線性化。因此忽略式(13)中的-bw×(Ibw)+Ga，得到如下簡化模型：

(17)

3 控制器設計

經典PID控制器不需要特定的模型參數，易于實現,是目前使用最多的控制算法[8]。PID控制器由比例單元P、積分單元I、微分單元D組成，分別對應目前誤差，過去累計誤差和未來誤差。

六旋翼控制器由外環的位置控制和內環的姿態控制組成。位置控制利用期望的位置解算得到期望的滾轉角、期望的俯仰角和期望的拉力。姿態控制利用期望的姿態角解算出期望的滾轉力矩、俯仰力矩和偏航力矩。

3.1 位置控制

位置控制原理是由期望的位置解算得到期望的滾轉角、俯仰角和期望的拉力[10]。

假設期望位置為pd=[xd,yd,zd]T測量值為p=[x,y,z]T，則位置誤差可以表示為ex=x-xd,ey=y-yd,ez=z-zd，控制器如下:

(18)

3.2 姿態控制

姿態控制利用期望的俯仰角θd、滾轉角φd、偏航角ψd解算出期望的俯仰力矩、滾轉力矩、偏航力矩，而期望的姿態角由位置控制模塊可以得到。

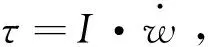
(19)

4 仿真分析

在MATLAB/Simulink環境中建立仿真模型如圖3，包含位置控制模塊，姿態控制模塊六旋翼動力學模塊。六旋翼參數如表1所列。

表1 六旋翼無人機參數

圖3 六旋翼控制仿真模型

給定目標位置(1，2，3)，初始位置為(0，0，0)，仿真結果如圖4～6。

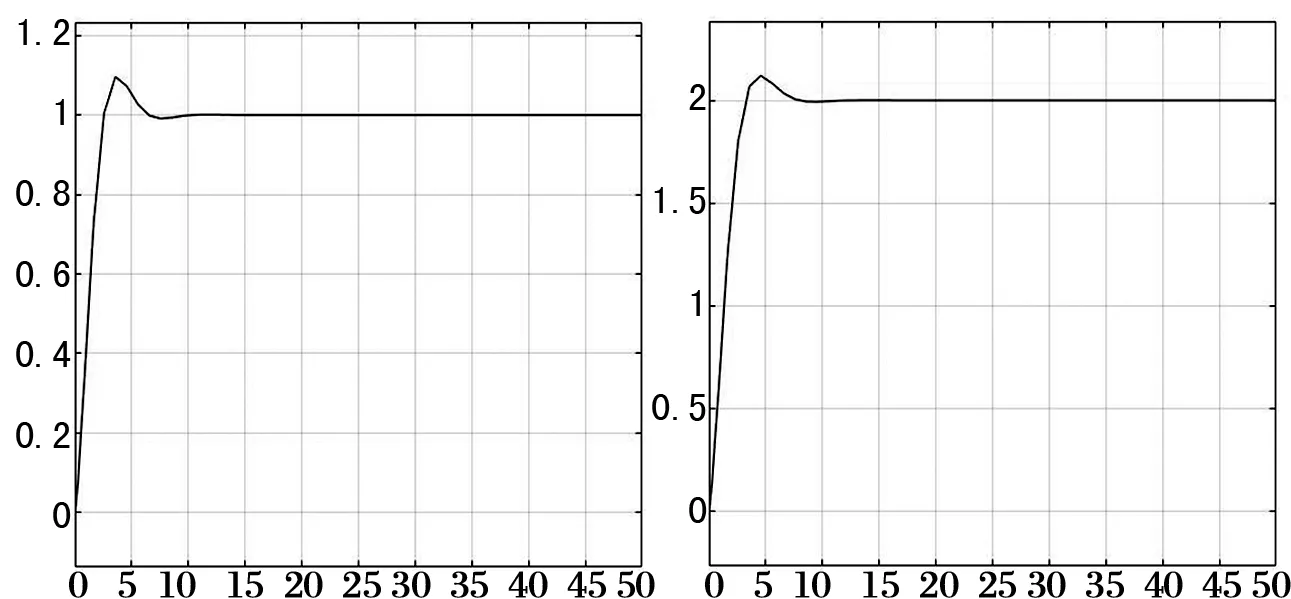
圖4 x方向位置變化

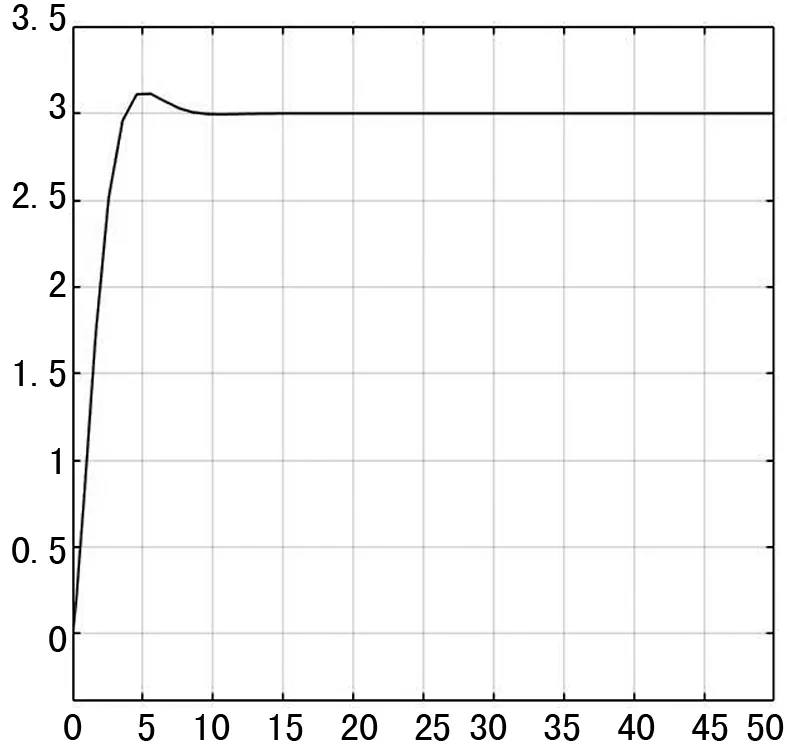
圖6 z方向位置變化

根據仿真結果可知，六旋翼從起飛到指定懸停位置用時10 s左右，響應速度符合預期。x方向的超調量為7.5%，y方向超調量為6.4%，z方向超調量為3.7%，均在可接受范圍內；穩態誤差約為0，表示能懸停在指定位置上。仿真驗證了PID控制的快速性及精確性。

5 結 語

建立了六旋翼無人機的動力學模型，并且對非線性模型進行了線性化處理，為了驗證模型的正確性，設計了位置PID控制器和姿態PID控制器。在MATLAB/Simulink中的仿真結果，實現了對六旋翼無人機的定點懸停控制，驗證了動力學模型的正確性和PID控制器的有效性，對后續控制系統的實驗具有參考意義。