GNSS模糊度整數估計方法圖形可視化軟件設計與應用分析

吳湯婷,劉麗晶,趙寶貴,盧立果

(1. 東華理工大學 江西省數字國土重點實驗室,江西 南昌 330013;2. 東華理工大學 測繪工程學院,江西 南昌 330013)

0 引 言

載波相位整周模糊度的快速準確解算是全球衛星導航系統(GNSS)實時高精度動態定位的關鍵問題,錯誤的整周模糊度將導致分米級甚至更大的定位偏差[1-4],而模糊度解算的核心在于模糊度浮點解的整數估計. 常用的三類模糊度整數估計方法包括:整數取整、整數序貫取整和整數最小二乘[5-10]. 盡管從理論上三類整數估計算法較容易被實現,且已有公開軟件LAMBDA3.0提供三類模糊度整數估計功能[11]. 但是單純地根據數學原理直接估計出整周模糊度,而對模糊度由實數空間映射到整數空間的過程缺乏直觀的認知,不利于對三類估計理論的深入理解. 為更好地解釋這三類整數估計過程,文獻[5-6]采用歸整域構建了模糊度實數域與整數域之間的幾何關系,文獻[7]進一步采用蒙特卡洛模擬了不同精度下模糊度的浮點解與歸整域之間的幾何關系,用以說明三類估計方法的性能. 盡管三類估計方法幾何原理清晰、圖形直觀,便于對三類整數估計原理的理解,但是實現過程較復雜,且目前尚未有公開軟件提供這類功能的演示. 因此,本文通過研究三類估計方法的一般理論表達式,基于MATLAB GUI設計了一套三類估計方法二維幾何圖形構建的可視化分析軟件,實現對三類估計方法的歸整域、映射圖和蒙特卡洛模擬及成功率計算等分析,為后續相關研究提供參考和幫助.

1 基本理論

1.1 歸整域

Sz={x∈Rn|z=F(x)},?z∈Zn,

(1)

式中,z為整數向量.

(2)

式中:sz(·)為指示函數,有

1.2 整數取整

整數取整(IR)估計是將模糊度浮點解向量的每個元素直接取整到最近的整數向量. 因此,IR估計不考慮模糊度分量間的相關性,其表達式為

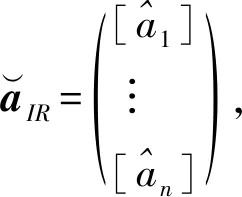
(3)

式中，[·]表示對元素進行取整運算；n=1, 2, 3, ….

由于IR是將模糊度浮點解直接歸整到最近的整數上,浮點解與整數解的差異值不超過0.5. 因此,IR估計的歸整域一般表達式為[6]

i=1,2…,n, ?z∈Zn,

(4)

式中，ci為第i個元素為1的單位坐標向量.

1.3 整數序貫取整

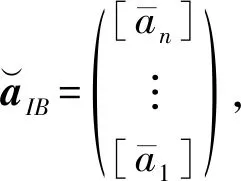
(5)

式中:

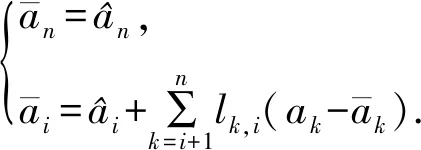
(6)

式中，lk,i為LTDL分解的單位下三角矩陣L的元素.

IB估計是將浮點解的條件期望取整到距其最近的整數,條件期望與取整的整數解的差異值不超過0.5. 因此,IB估計的歸整域一般表達式為[6]

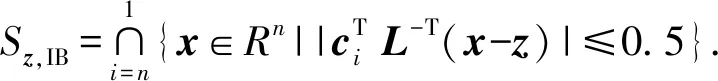
(7)

1.4 整數最小二乘

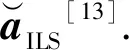
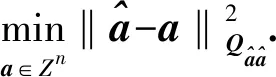
(8)

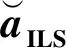
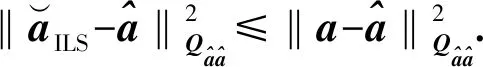
(9)

因此,ILS歸整域一般表達式為[5]

?z,u∈Zn,z≠u,

(10)

式中:x為浮點解;z為ILS解;u為任一整數向量.

式(10)可以進一步簡化為

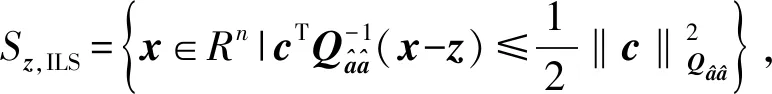
(11)

式中:c=u-z.

由式(11)可知,ILS歸整域是由多個平面圍成的空間,且平面數取決于模糊度次優解個數,模糊度次優解個數區間為[2n, 2n+1-2]．

2 三類整數估計方法歸整域演示軟件設計

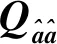
圖1為三類整數估計方法圖形可視化軟件功能結構圖，圖2為三類整數估計圖形可視化軟件界面.

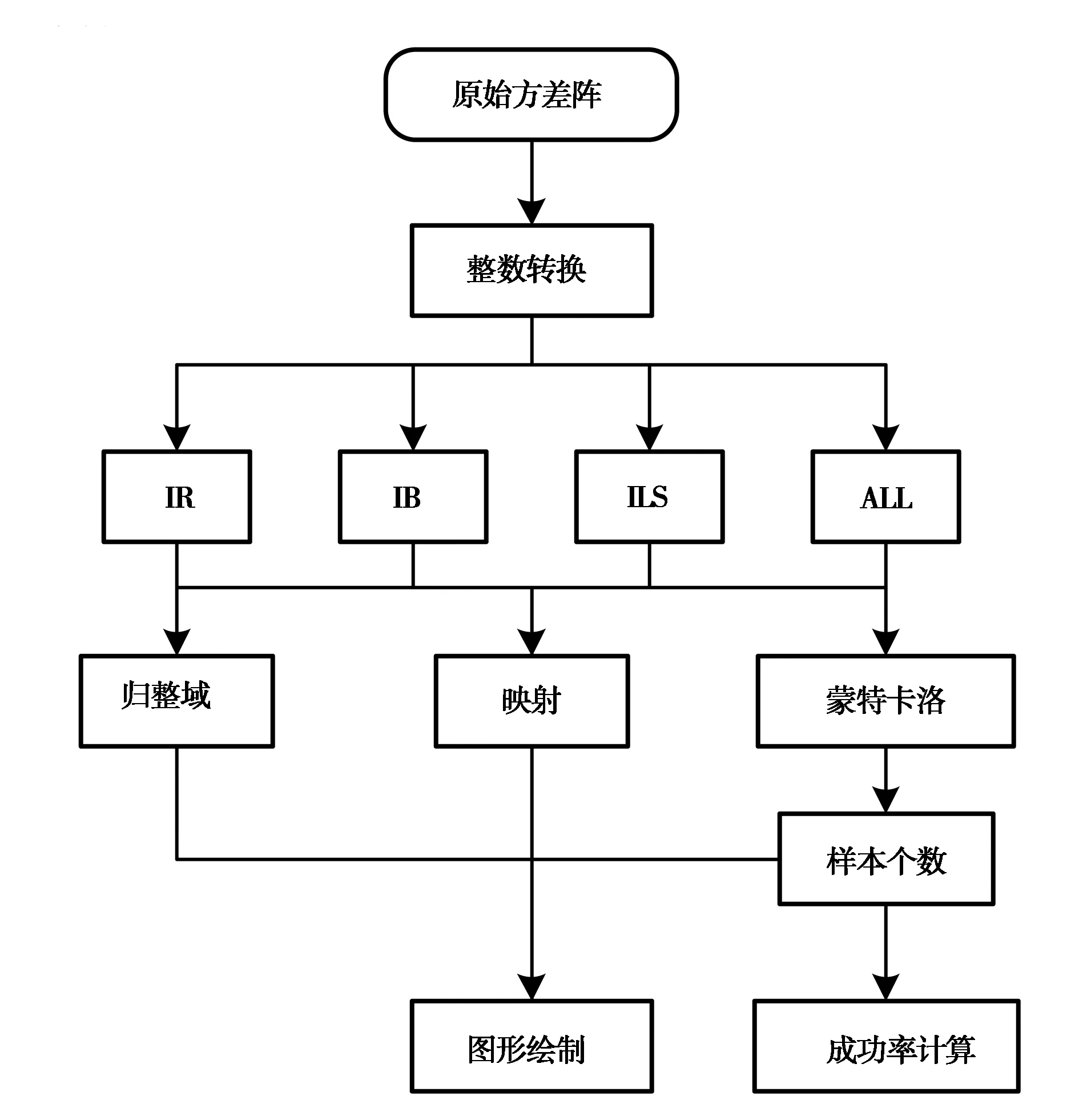
圖1 三類整數估計方法圖形可視化軟件功能結構圖.

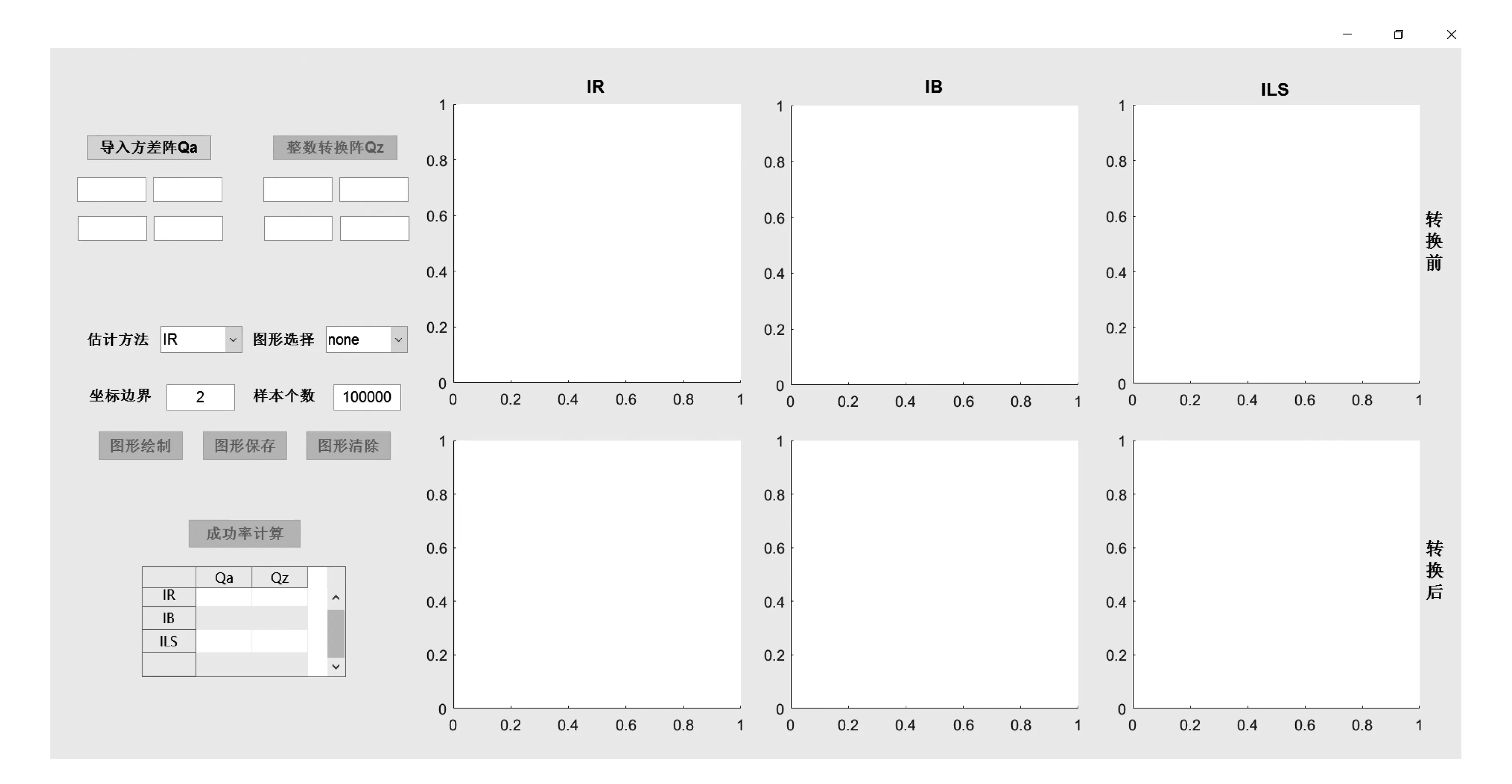
圖2 三類整數估計方法圖形可視化軟件界面.

3 軟件測試與分析

3.1 歸整域圖

圖3為繪制的IR歸整域圖.從圖中可以看到IR的二維歸整域是由規則的正四邊形構成的實數空間. 分析其原因為IR估計僅與浮點解有關,取整過程可以看作是浮點解的四舍五入,因此對于二維模糊度來說,其歸整域是一個規則的正四邊形,且整數轉換前后不改變其形狀.

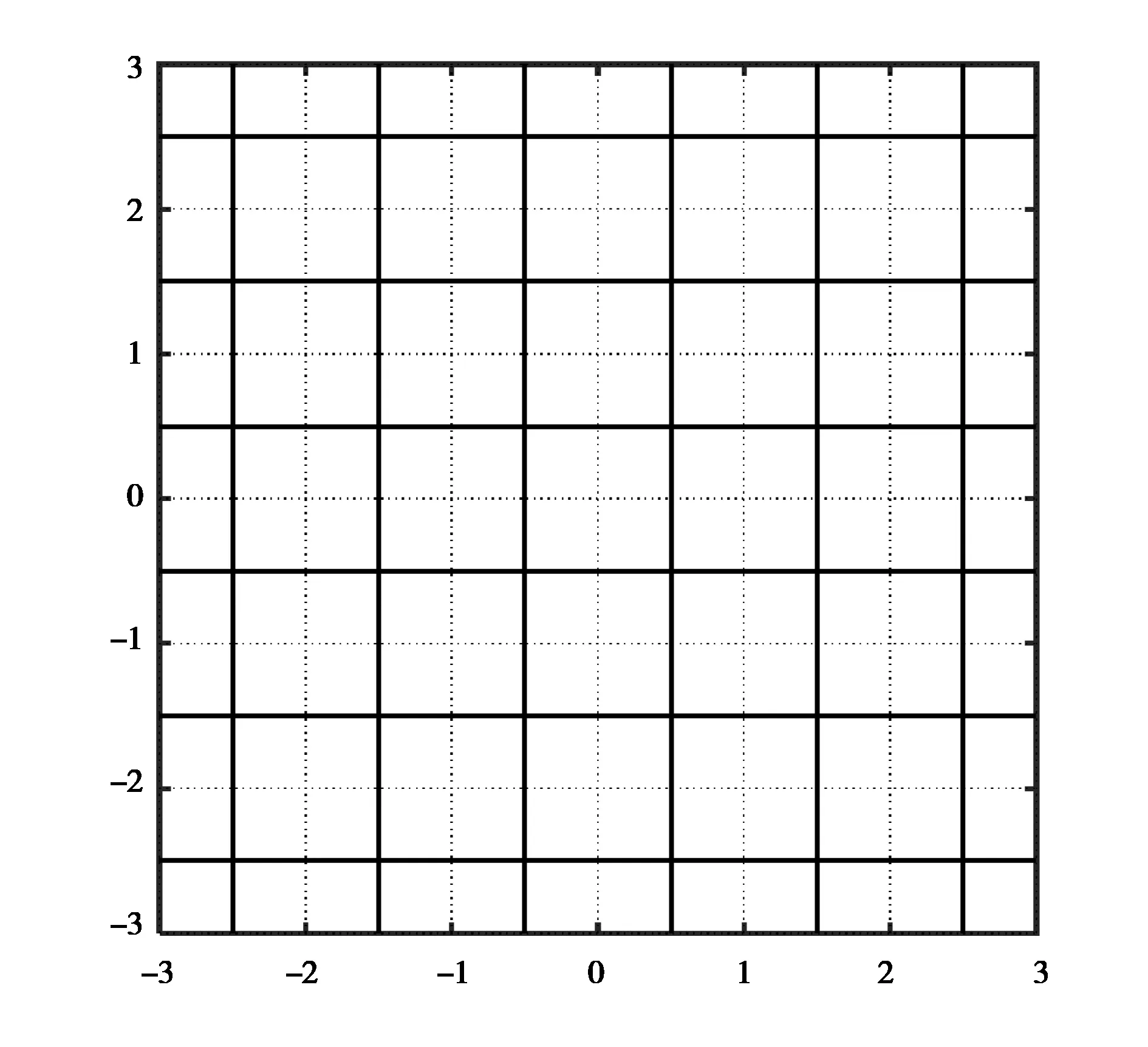
圖3 IR歸整域圖形

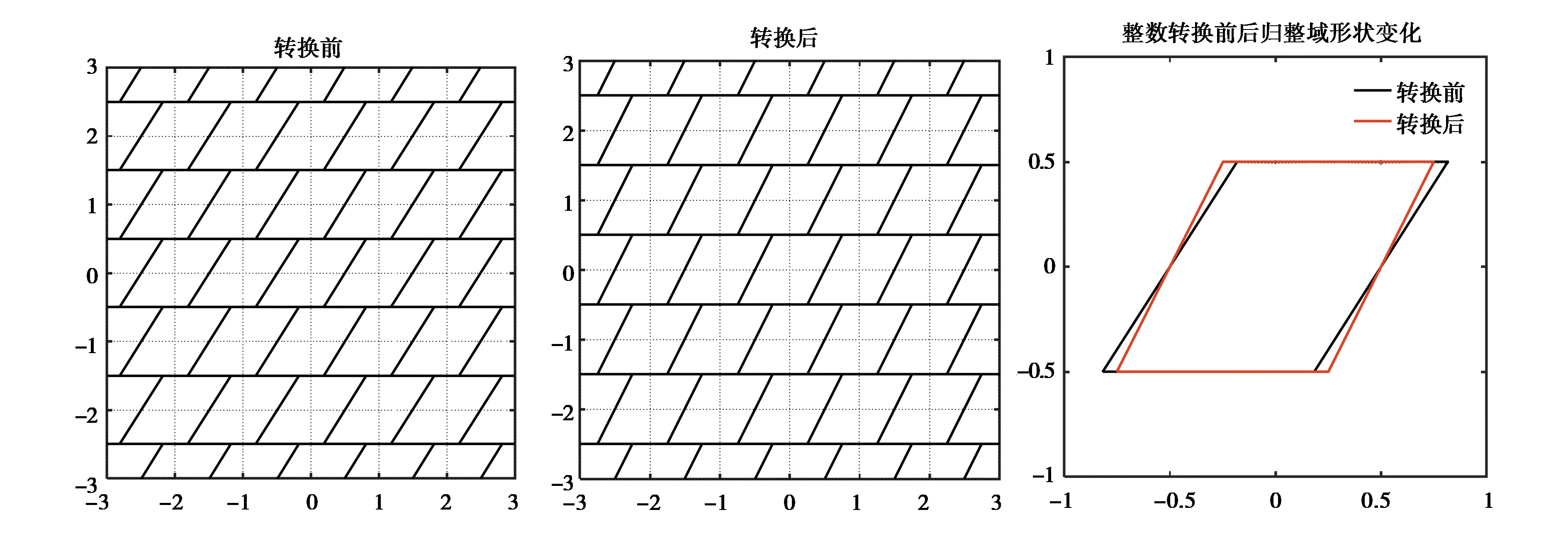
圖4 IB轉換前后歸整域圖形及其形狀變化圖

圖4為繪制的IB整數轉換前后歸整域及其變化圖.由圖可見IB的歸整域為一個平行四邊形,轉換后的形狀相對于轉換前更接近正四邊形. 分析其原因為基于LTDL分解的IB估計是由后到前的順序進行序貫取整,因此對于二維模糊度向量來說,第一個估計的模糊度分量(即Y軸方向)是按照直接取整獲得的,第二個估計的模糊度分量(即X軸方向)是基于式(4)序貫取整得到的,其取整范圍受模糊度分量間的相關性影響,但是每一個歸整域在X軸方向的邊界范圍大小仍為1,此時歸整域為平行四邊形. 當模糊度分量不存在相關性時,IB估計等同于IR估計,此時IB的歸整域簡化為正四邊形. 由于整數轉換的中間過程可以有效地降低模糊度分量間的相關性,因此轉換后的形狀將更接近正四邊形.

圖5為繪制的ILS轉換前后歸整域及其形狀變化圖.由圖可以看到轉換前由于模糊度分量間相關性很大,ILS的歸整域是一個狹長的凸六邊形,轉換后的歸整域為一個比較規則的凸六邊形. 分析其原因為ILS是基于最小二乘搜索獲得最優解(即ILS解),而對于同一個最優解當浮點解選取不同時將會對應不同的次優解,由式(10)可知其歸整域的構建取決于次優解和最優解之間的線性關系. 對于二維模糊度向量來說,通常根據浮點解的選取不同最優解對應六個次優解,此時歸整域為六條直線構成的交叉區間. 需要說明的是,當模糊度分量線性無關時,ILS估計等同于IR估計,此時歸整域簡化為正四邊形. 對于原始的模糊度向量,由于模糊度分量間的相關性很大,此時歸整域是一個狹長的凸六邊形;而整數轉換的中間過程可以有效地降低模糊度分量間的相關性,此時轉換后的形狀將朝著接近正四邊形的方向變化.

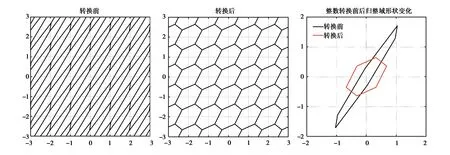
圖5 ILS轉換前后歸整域圖形及其形狀變化圖

3.2 映射圖

圖6為整數轉換后三類估計方法映射圖.其中,模糊度真值假定為零向量. 由圖可知,每個整數向量對應唯一的歸整域,且各歸整域之間互不重疊,當采用IR、IB和ILS估計時,浮點解處于零向量所在的歸整域才能獲得正確值,反之則會錯誤固定. 因此,三類估計方法的模糊度浮點解和固定解在歸整域內滿足“多對一”的映射關系.

圖6 整數轉換后三類估計方法映射圖(綠色點為真值，紅色點為錯誤值)

3.3 蒙特卡洛模擬浮點解圖

圖7為蒙特卡洛模擬生成的浮點解與三類歸整域的關系圖.其中,模擬樣本數為10 000. 由圖可見,整數轉換前浮點解分布在一個傾斜的扁形橢圓空間內,整數轉換后浮點解分布在一個近似圓形的橢圓空間內,主要是由于整數轉換通過降低模糊度相關性實現了橢球的壓縮. 在三類歸整域與浮點解空間分布的關系方面,ILS在整數轉換前后歸整域均與浮點解分布形狀保持最大程度的吻合,IB次之,IR最差,且IB和IR與整數轉換直接相關,整數轉換有利于增大二者的吻合程度.

3.4 成功率計算

表1所示為整數轉換前后三類方法模糊度正確估計的概率.其中,成功率=落在歸整域內樣本數/總樣本數,為保證成功率統計的準確性盡量不受蒙特卡洛模擬樣本個數的影響,樣本數設定為10 000 000. 由表1可知，整數轉換前,IR和IB的成功率遠低于ILS,整數轉換后IR和IB的成功率得以較大程度地提高,ILS成功率不受整數轉換的影響,三類方法模糊度估計的成功率大小滿足不等關系:PS,IR≤PS,IB≤PS,ILS,統計結果與文獻[14]理論相符. 根據成功率統計式,由圖7也能很直觀得出上述不等關系.

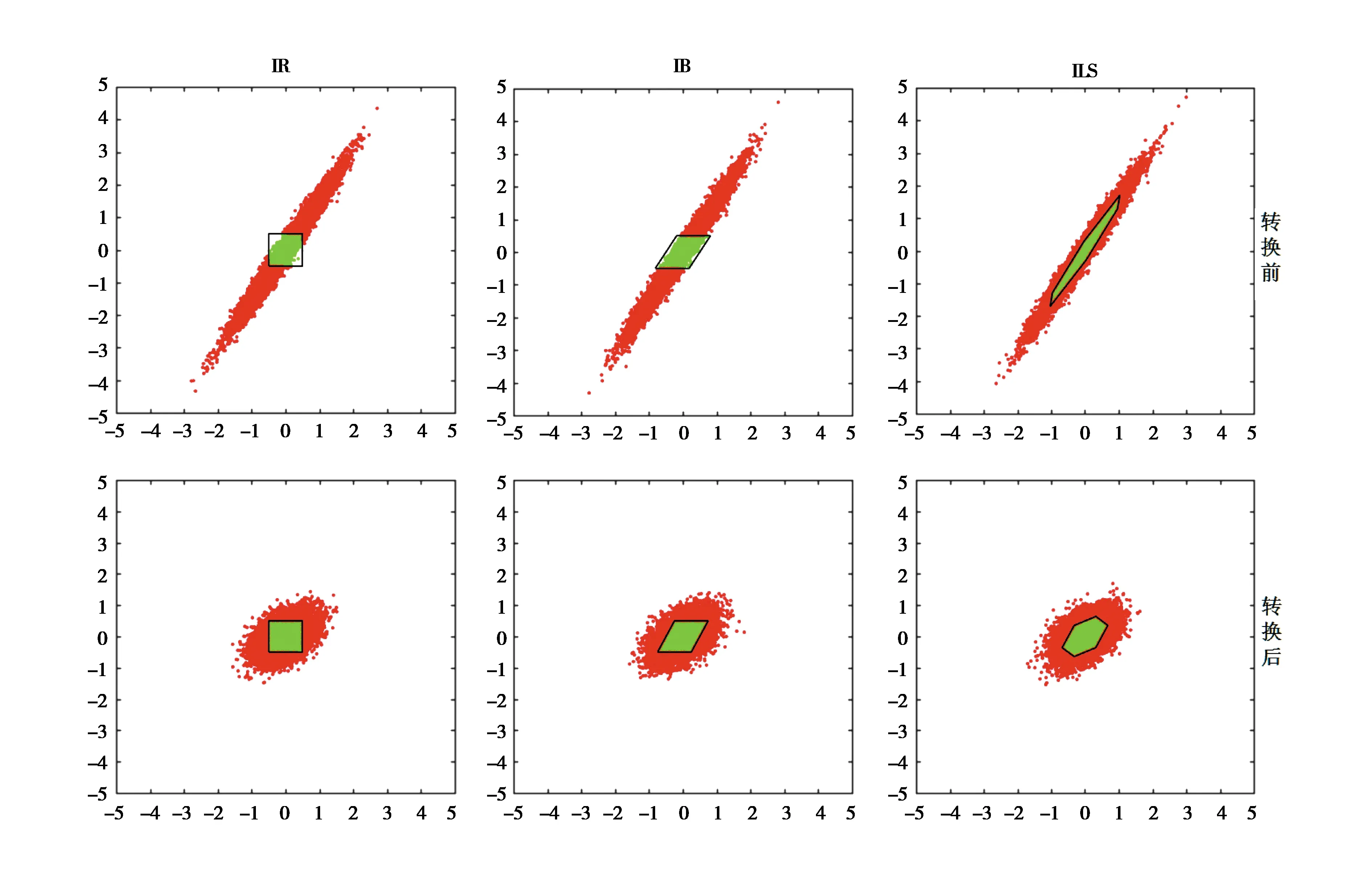
圖7 蒙特卡洛模擬浮點解與三類歸整域的關系圖

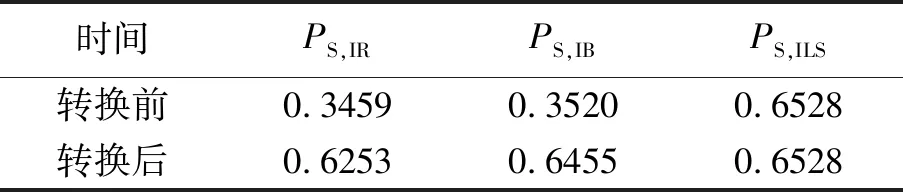
表1 三類估計方法成功率

4 總 結

針對IR、IB和ILS三類估計方法由浮點解到整數解的固定過程過于抽象,不利于對整數估計的直觀理解這一問題. 本文基于MATLAB GUI設計了一套三類估計方法二維幾何圖形構建的可視化分析軟件. 該軟件可以實現三類估計方法的歸整域構建、浮點解與固定解間的映射圖構建、不同精度下浮點解的蒙特卡洛模擬以及成功率計算等功能. 實驗測試數據表明該軟件性能穩定,可以滿足對三類整數估計方法幾何圖形表達的需求,并有助于直觀形象地理解整數轉換對模糊度估計的影響,也對模糊度估計方法的教學演示具有很好的輔助作用.