基于蟻群優化K均值聚類算法的滾軸故障預測

陳湘中，萬爛軍+，李泓洋，李長云

(1.湖南工業大學 計算機學院，湖南 株洲 412007；2.湖南工業大學 智能感知與網絡化控制湖南省高校重點實驗室，湖南 株洲 412007)

0 引 言

滾軸是機器中的易損部件，是否能夠準確地診斷出其發生了何種故障及故障程度，對于滾軸的健康維護和安全運行是非常重要的，目前已經研發了多種滾軸故障診斷方法[1-5]。經驗模態分解[1,2]是常用的軸承故障診斷方法之一，該方法是直觀和后驗的，但在使用過程中易產生過包絡、欠包絡以及端點效應等問題。

聚類算法是一種非監督學習方法，而K均值聚類算法[3,6,7]是最為經典的基于劃分的聚類方法，采用距離作為相似性的評價依據，距離越近，則相似度就越大。孟凡磊等[3]結合局部特征尺度分解與K均值聚類分析對滾軸進行故障診斷，該方法是經驗模態分解的改進，解決了過(欠)包絡的問題。但K均值聚類算法通常隨機選擇K個初始的聚類中心來確定一個初始劃分，一旦初始聚類中心選取不合理，就容易陷入局部最優解。蟻群優化(ant colony optimization，ACO)算法具有強大的全局尋優性和適應能力強等優點，該算法已廣泛應用在多個研究領域[8-11]。蟻群優化算法的全局尋優性可彌補傳統K均值聚類算法隨機選擇初始聚類中心的缺陷，從而使得聚類效果更佳。

鑒于此，在傳統K均值聚類算法的基礎上，提出一種基于蟻群優化K均值聚類算法的滾軸故障預測方法，針對西儲大學的滾軸數據集進行測試，結果表明所提方法能有效提高滾軸故障預測的準確率和穩定性。

1 基本理論

1.1 蟻群優化算法概述

ACO算法的靈感來自對真實蟻群覓食行為的觀察，螞蟻常常可以找到食物源頭與螞蟻巢穴之間的最短距離，這是通過螞蟻攝入食物所沉淀的稱為信息素的化學物質來實現的[8]。螞蟻利用自己對食物氣味來源的知識(啟發素)和對食物路徑的決定(信息素)來搜索路徑。螞蟻在路徑搜索過程中，通過存放自己的信息素來確定路徑，這會使得信息素蹤跡越來越密集，更有可能被其它螞蟻選擇。這是一種學習機制，螞蟻根據自己對路徑的認識，最佳路徑將從巢穴向食物標記。

如圖1所示，假設螞蟻想從A點移動到B點，若無障礙物，它們將沿直線路徑(AB)移動(圖1(a))。若存在障礙物，螞蟻將隨機地轉向左(ACB)或轉向右(ADB)(圖1(b))。由于ADB路徑比ACB路徑短，沉積在ADB路徑上的信息素的強度大于ACB路徑，故吸引了更多的螞蟻來到此路徑(圖1(c))。

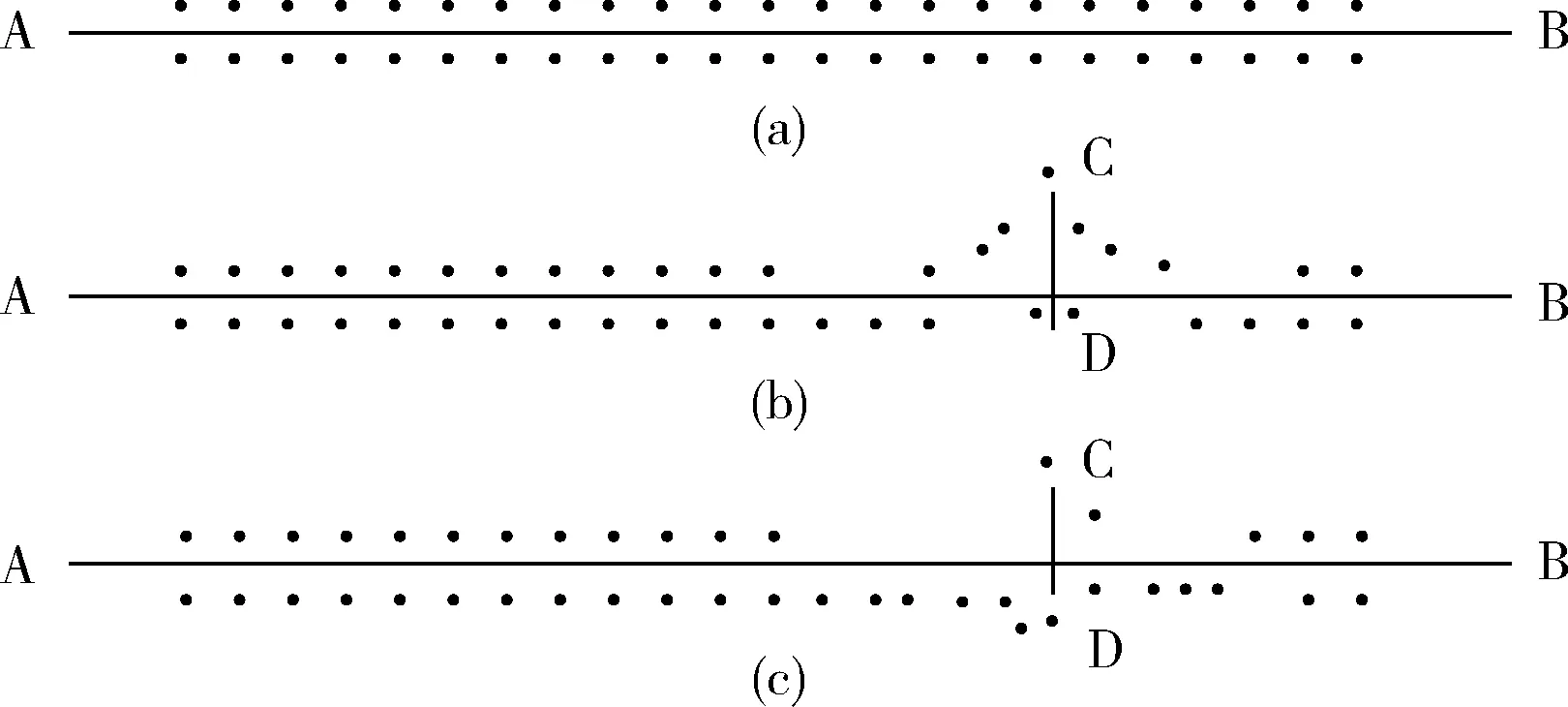
圖1 螞蟻尋找最短路徑示例

1.2 K均值聚類算法概述

K均值聚類起源于信號處理，是最經典的聚類分析方法，K均值聚類的核心目標是將給定的樣本集D={x1,x2,…,xm} 劃分成k個簇，并給出每個樣本對應的簇中心點[7]。該算法的步驟如下：

步驟1 數據預處理，如歸一化等。

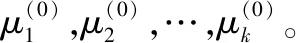
步驟3 定義代價函數，如式(1)所示

(1)

步驟4 令t=0,1,2,…為迭代次數，重復步驟5和步驟6，直到J收斂。

步驟5 對于每一個樣本xi，根據式(2)將其分配到距離最近的簇

(2)

步驟6 根據式(3)重新計算每個類簇的聚類中心

(3)

K均值聚類算法在迭代時，若當前J還不是最小值，先固定簇中心 {μk}，通過調整每個樣本xi所在的類簇ci來讓J變小；然后固定 {ci}，通過調整簇中心 {μk} 使J變小。交替循環這兩個過程，J單調遞減：當J達到最小值時，{μk} 和 {ci} 均將收斂。

2 基于蟻群優化K均值聚類算法的故障預測方法

本文提出的滾軸故障預測方法主要由基于小波包分解的數據預處理、特征向量歸一化和基于蟻群優化K均值聚類算法的故障預測模型訓練這3部分組成，滾軸故障預測流程如圖2所示。

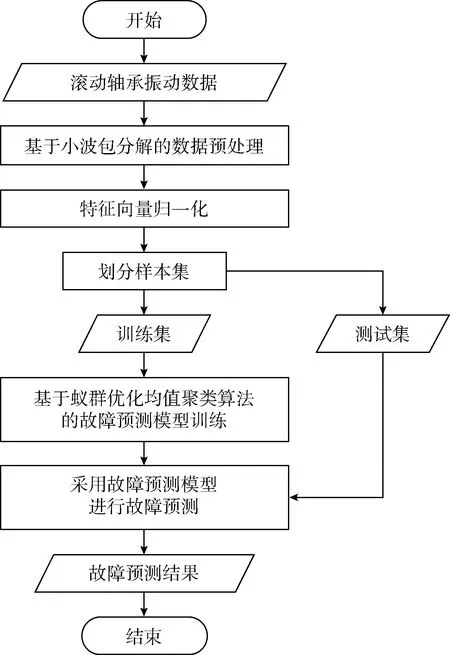
圖2 滾軸故障預測流程

在滾軸故障預測中，首先對滾軸原始振動數據進行小波包分解，得到特征向量；接著對特征向量進行歸一化，得到樣本集；然后將樣本集劃分為訓練集和測試集。針對訓練集中的數據，采用蟻群優化K均值聚類算法進行滾軸故障預測模型的訓練，得到滾軸故障預測模型；然后采用滾軸故障預測模型對測試集中的數據進行測試，根據得到故障預測結果驗證故障預測模型的有效性。

2.1 基于小波包分解的數據預處理

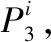
(4)

滾軸原始振動信號經小波包分解后，得到多個由8個頻段能量值構成的特征向量，這些特征向量可作為K均值聚類算法的輸入。

2.2 特征向量歸一化

為了提高滾軸預測模型的訓練速度，將滾軸振動數據經三層小波包分解后得到的特征向量按式(5)進行歸一化

(5)

式中：xi(i=1,…,8) 是特征向量中第i個頻段的能量值，xmax是特征向量中的最大值，xmin是特征向量中的最小值，x′i是第i個頻段歸一化后的結果。

2.3 故障預測模型訓練

故障預測模型訓練流程如圖3所示，首先初始化螞蟻數量、集群數量和信息素值；其次為每個集群隨機初始化集群中心；然后根據振動數據的特征向量和聚類中心之間的距離(相似性)成反比的概率以及表示信息素水平的變量τ，將每個滾軸特征向量分配給集群。接下來，不斷更新聚類中心，當迭代次數大于1000或者迭代次數大于50且收斂方案重復次數大于20的時候，終止算法得出最佳解決方案。

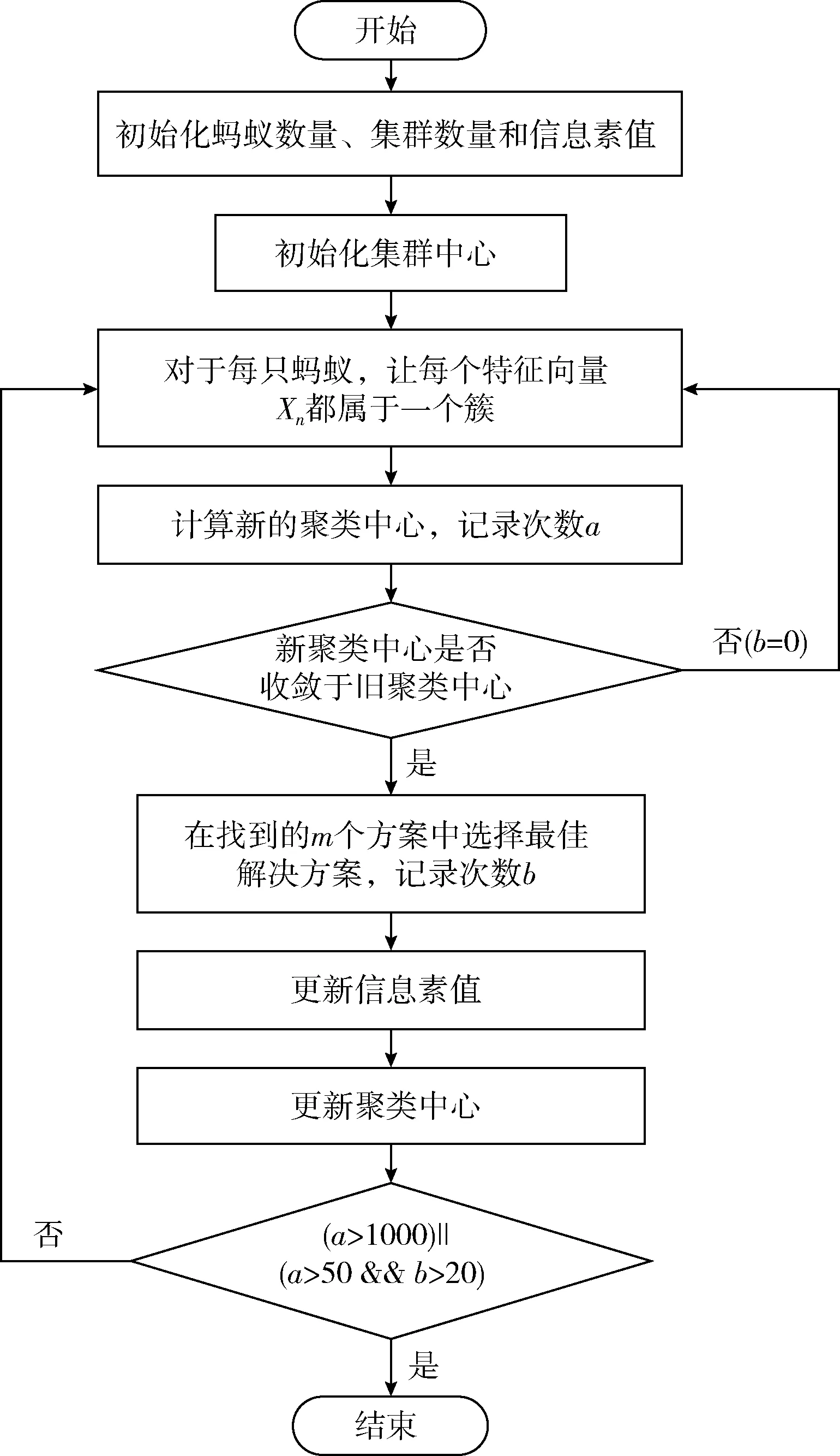
圖3 故障預測模型訓練流程

在基于蟻群優化的K均值聚類算法中，聚類工作由眾多螞蟻協同執行，對于每只螞蟻，讓每個特征向量Xn都屬于一個簇。根據信息素τ和啟發信息η，每只螞蟻將每個特征向量分配給簇i的概率為P，其計算公式如式(6)所示

(6)

式中：P(i,Xn)是在簇i中選擇特征向量Xn的概率，τ(i,Xn)是分配給簇i中特征向量Xn的信息素，α是控制τ(i,Xn)的影響的參數；η(i,Xn)是分配給簇i中特征向量Xn的啟發信息，β是控制η(i,Xn)的影響的參數。啟發信息η(i,Xn)來自式(7)

(7)

式中：Ci是簇i的聚類中心，其中d(Xn,Ci) 是滾軸特征向量Xn和聚類中心Ci的歐氏距離。通過計算每個集群中滾軸振動數據的特征向量的平均值來獲取新的聚類中心，這將重復進行，并保存迭代次數a的值。再判斷新的聚類中心是否收斂于舊的聚類中心，不收斂則將收斂方案重復次數b的值置為0。若收斂則在找到的m個方案中選擇幾率最大的解決方案作為最佳解決方案，并根據式(8)更新信息素值

τ(i,Xn)=(1-ρ)τ(i,Xn)+∑iΔτ(i,Xn)

(8)

式中：ρ是信息素揮發因子 (0<ρ≤1)，這表示早期的信息素將在迭代中消失。隨著更好的解決方案不斷被發現，相應的信息素也不斷被實時更新，其信息素對下一個解決方案具有更大影響。Δτ(i,Xn)在式(8)中是由成功的螞蟻添加到先前信息素的信息素量，其計算公式如式(9)所示

(9)

式中：Q是一個常數，它與螞蟻添加的信息素的數量有關；Min(k′) 是螞蟻k′得到的每兩個簇中心之間最小距離的和；Avgd(k′,i) 是螞蟻k′得到的每個特征向量與其簇心之間距離的平均和。

3 實 驗

3.1 實驗數據集及實驗平臺

為驗證本文提出的基于蟻群優化K均值聚類算法的滾軸故障預測方法的有效性，對西儲大學的滾軸數據集[12]進行了測試。本實驗使用了40個測試數據集，其中正常數據集4個、滾動體故障數據集12個、內圈故障數據集12個和外圈故障數據集12個。每個數據集包含10多萬條滾軸振動數據，這些數據是在電機轉速為每分鐘1720轉至1797轉以及采樣頻率為12 kHz的工況下采集的原始振動數據。

實驗平臺：一臺搭配了四核Intel Xeon E3-1225 v5 CPU和32 GB內存的HP Z240 SSF工作站，Win 7系統和Matlab 2014a。

3.2 振動數據特征提取

使用小波包分解對滾軸振動數據進行特征提取，每種運行狀態分別得到由8個頻段能量值組成的特征向量，特征提取部分數據見表1。

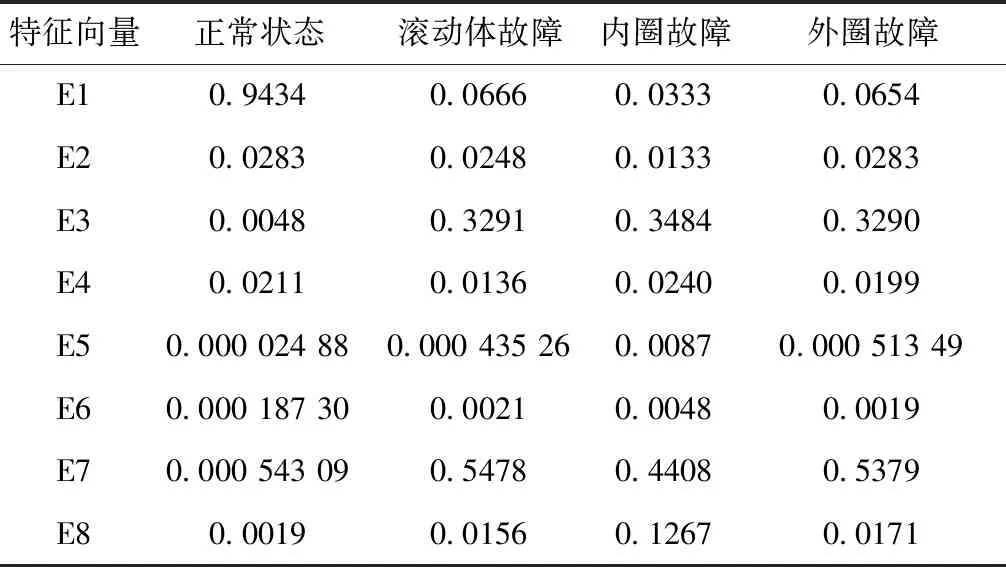
表1 特征提取部分數據

圖4-圖7是滾軸原始振動信號經小波包分解后得到的能量譜，顯而易見，對于滾軸的不同運行狀態，其能量分布有所不同。在滾軸正常運行狀態下，其能量分布主要集中在第1頻段，滾軸正常信號能量譜如圖4所示。在滾軸滾動體故障下，其能量分布主要集中在第1、3、7頻段，滾軸滾動體故障信號能量譜如圖5所示。在滾軸內圈故障下，其能量分布主要集中在第3、7頻段，在第1、2、4、8頻段也有少部分能量分布，滾軸內圈故障信號能量譜如圖6所示。在滾軸外圈故障下，其能量分布主要集中在第3、7頻段，滾軸外圈故障信號能量譜如圖7所示。

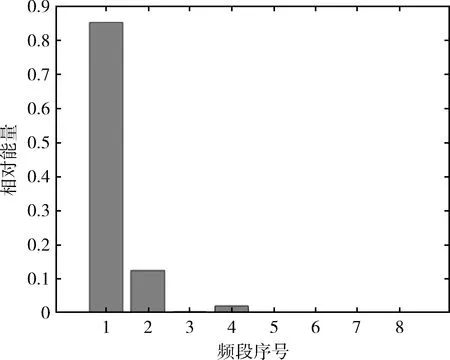
圖4 滾軸正常信號能量譜

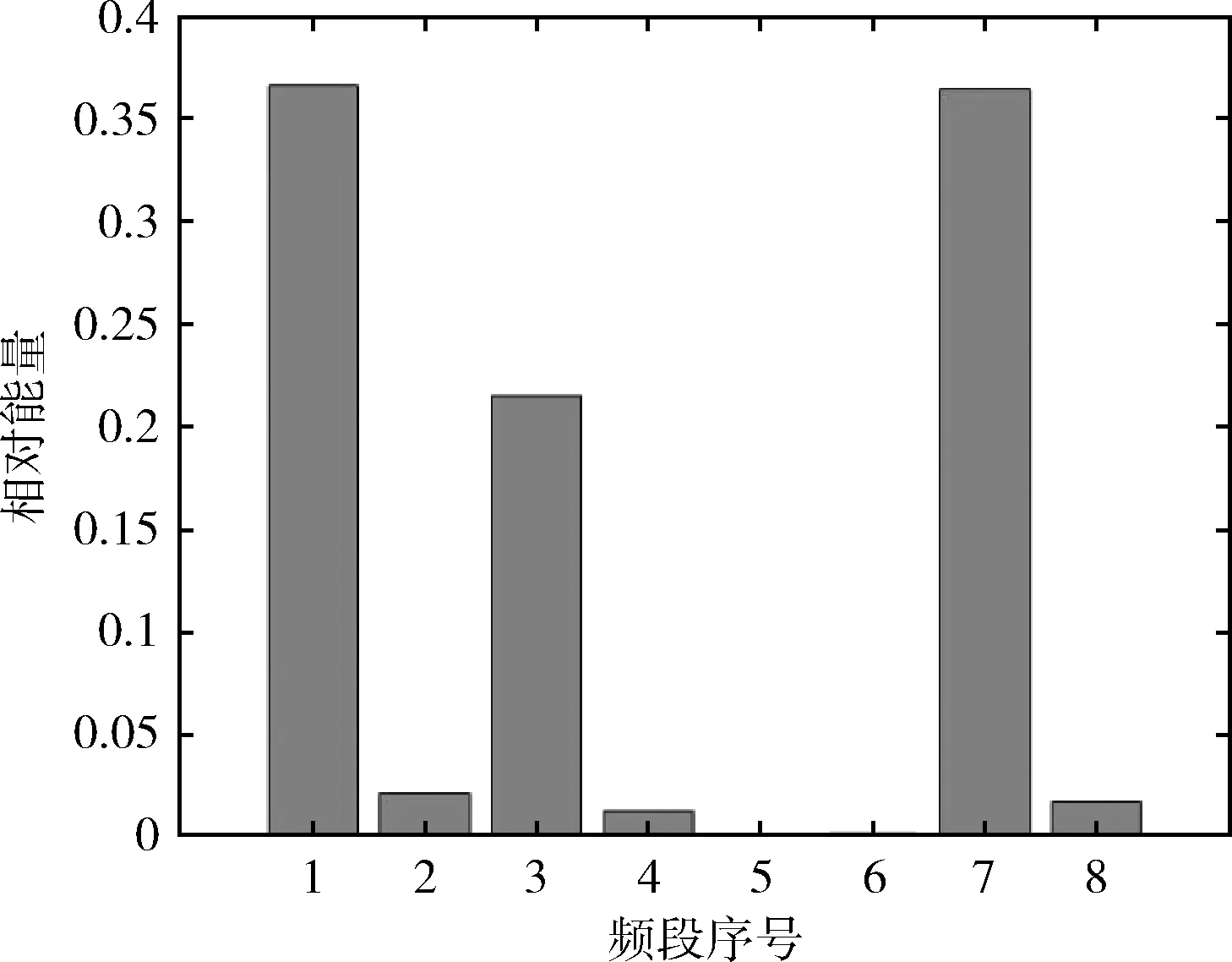
圖5 滾軸滾動體故障信號能量譜

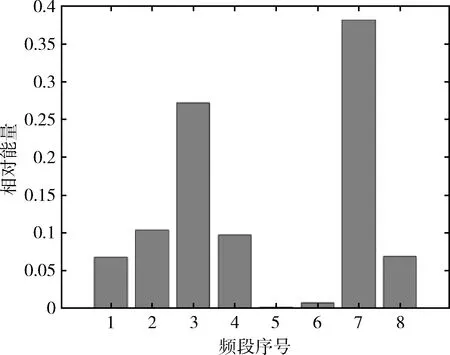
圖6 滾軸內圈故障信號能量譜

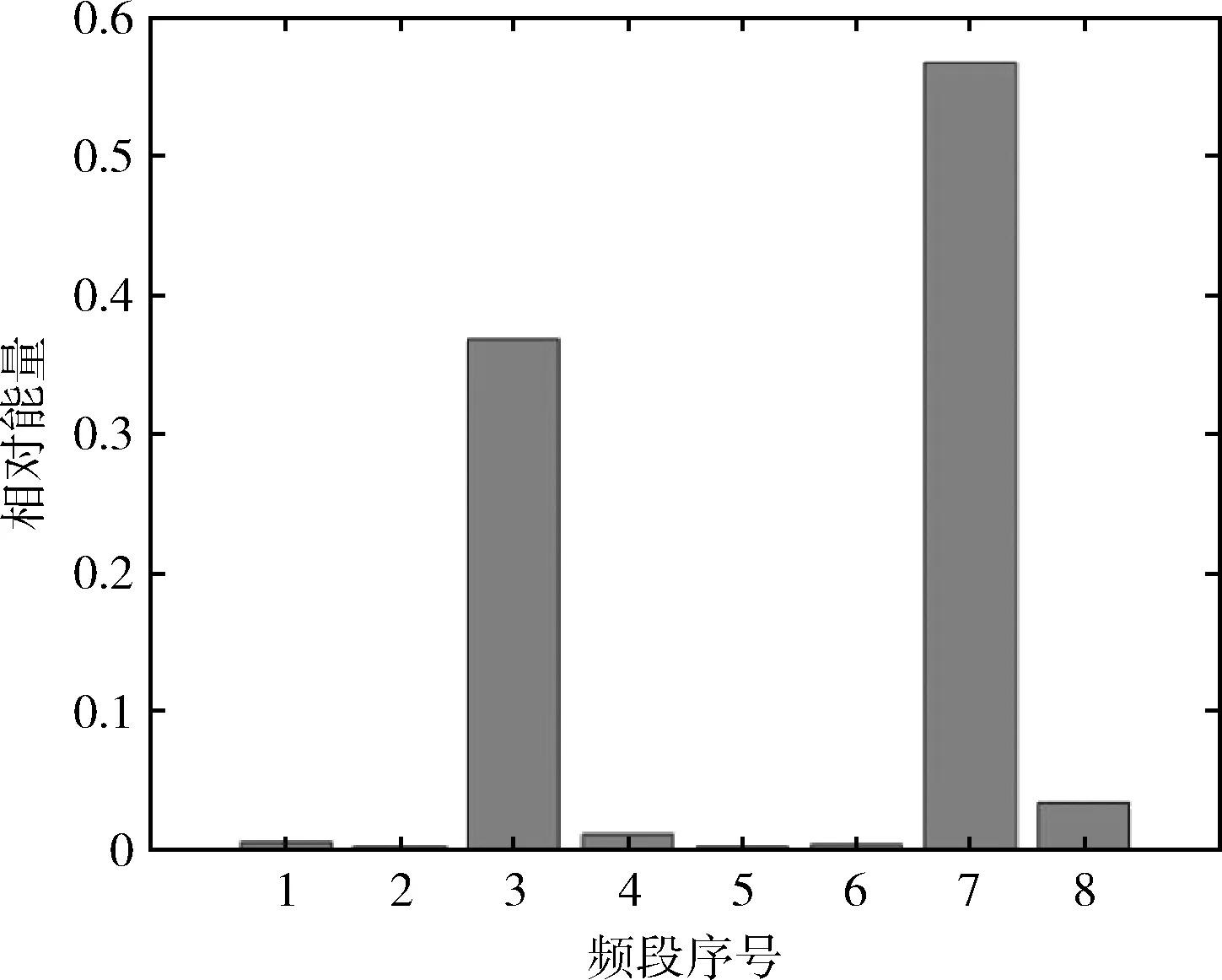
圖7 滾軸外圈故障信號能量譜

3.3 實驗結果分析

本實驗選擇了兩種不同的算法：傳統的K均值聚類算法(K-Means)以及蟻群優化K均值聚類算法(ACO-K-Means)，使用滾軸故障預測模型對測試集進行實驗，計算兩種算法各自100次實驗的平均故障預測準確率。實驗參數設置見表2。

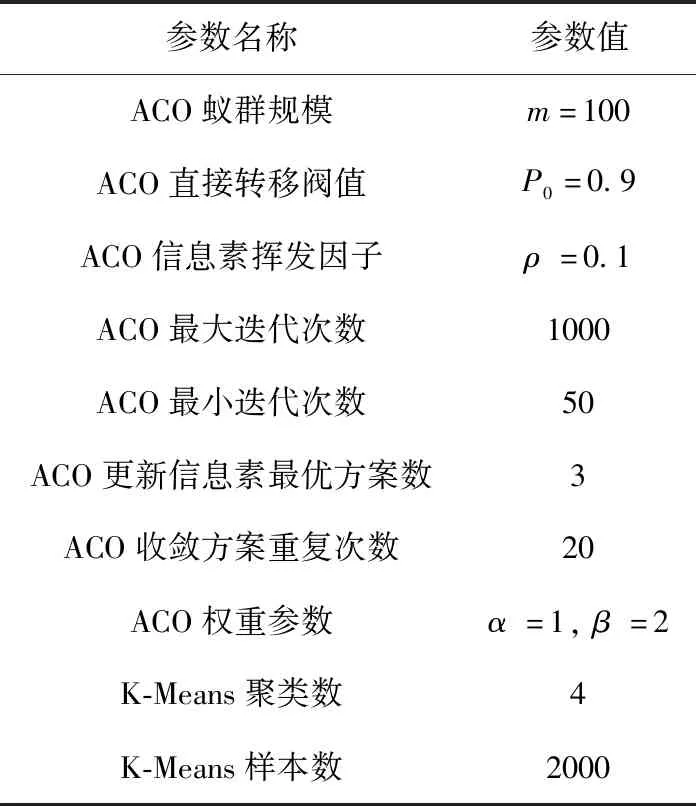
表2 實驗參數設置

兩種算法對應的滾軸故障預測準確率如圖8所示，采用傳統K均值聚類算法得到的故障預測準確率為91.87%，而采用ACO-K-Means得到的故障預測準確率達到了97.76%。采用傳統K均值聚類算法可能得到局部優化，而采用蟻群優化K均值聚類算法更可能得到全局優化。

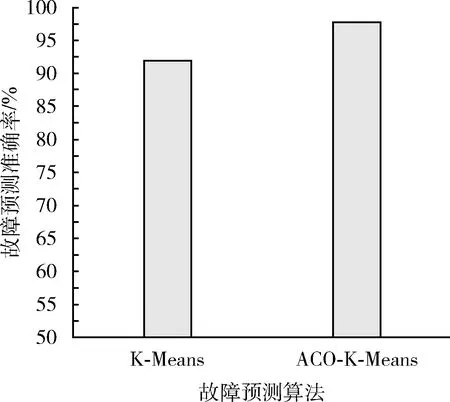
圖8 兩種算法對應的滾軸故障預測準確率

使用傳統K均值聚類算法得到的4個聚類中心和它們分別對應的8個特征向量見表3，使用蟻群優化K均值聚類算法得到的4個聚類中心和它們對應的8個特征向量見表4。表3和表4中“1”是滾動軸正常運行狀態的聚類中心，“2”是滾軸滾動體故障的聚類中心，“3”是滾軸內圈故障的聚類中心，“4”是滾軸外圈故障的聚類中心。與表3比較，表4的聚類中心“2、3、4”均有變化。此外，也可通過更加直觀的聚類效果圖來進行對比，如圖9和圖10所示。

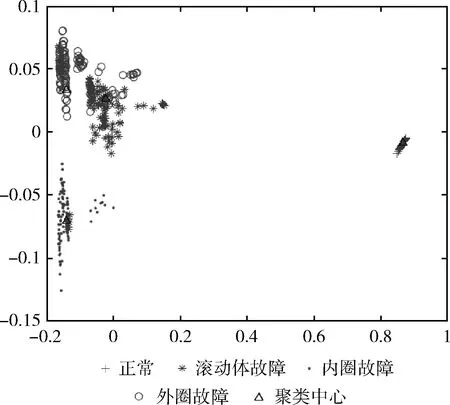
圖9 使用K-Means得到的聚類效果

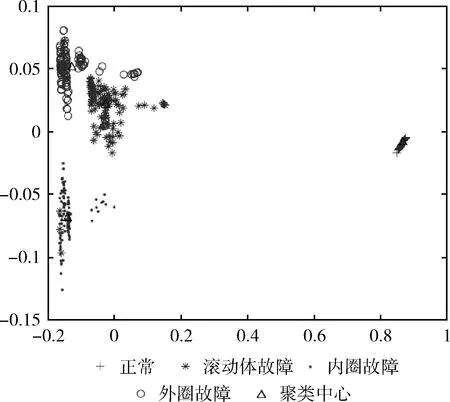
圖10 使用ACO-K-Means得到的聚類效果

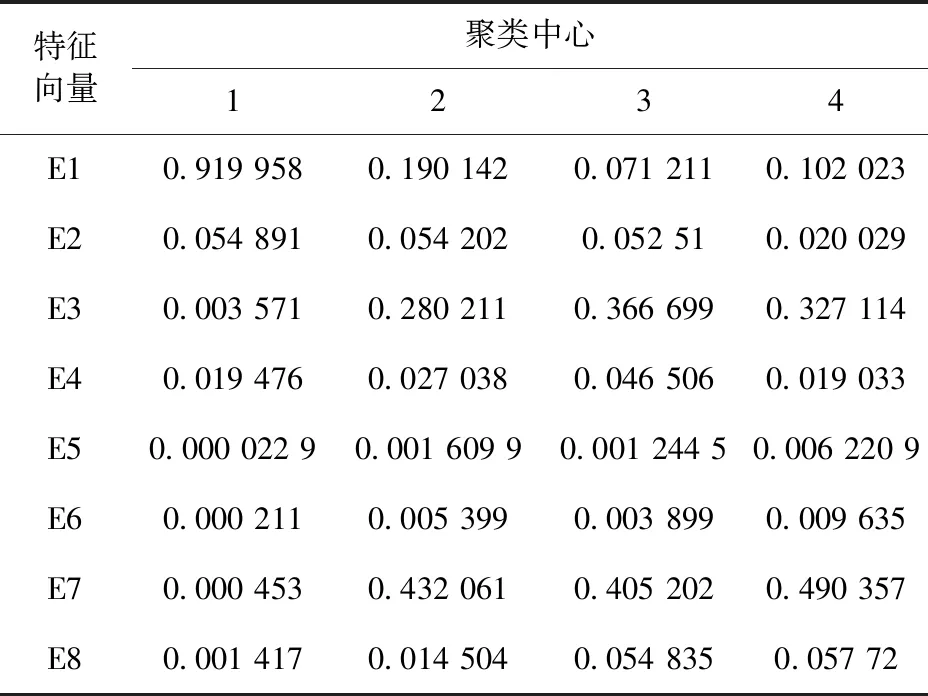
表3 使用K-Means得到的聚類中心對應的特征向量

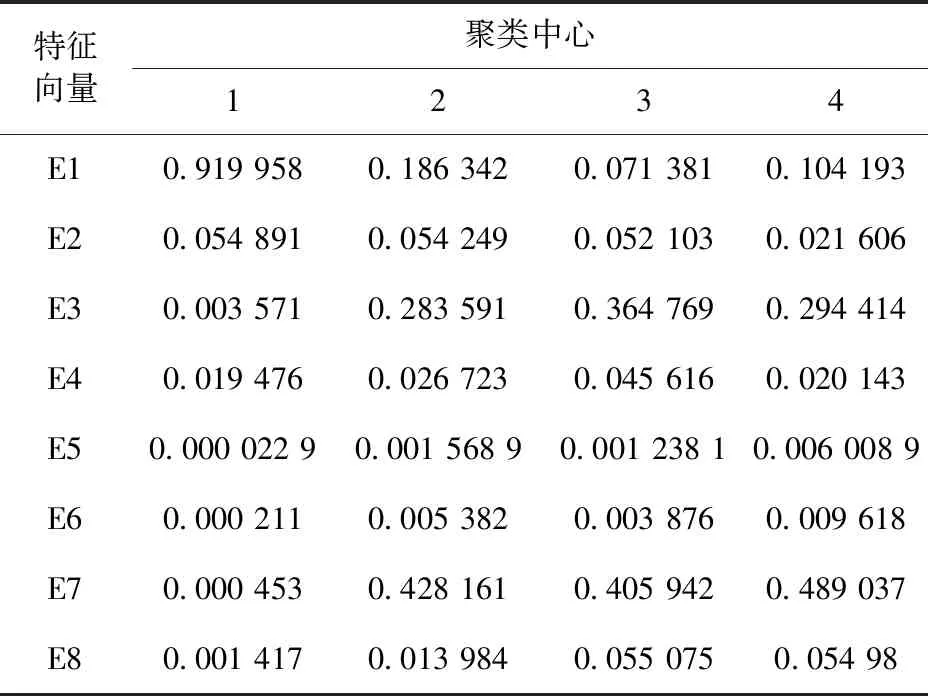
表4 使用ACO-K-Means得到的聚類中心對應的特征向量

使用傳統K均值聚類算法得到的聚類效果如圖9所示，可以看出滾軸正常狀態和內圈故障的聚類效果較明顯，但滾動體故障和外圈故障的聚類效果卻不是很理想，這是因為這兩類故障的特征向量比較相似，聚類中心距離較近，反應出的樣本整體效果很可能是局部最優，導致故障預測效果不佳。

使用本文提出的蟻群優化K均值聚類算法得到的聚類效果如圖10所示，與圖9相比，可以看出滾軸外圈故障和滾動體故障的聚類中心有較明顯的變化，使用蟻群優化K均值聚類算法能得到更優的聚類中心，從而獲得更穩定和更高的故障預測準確率。

4 結束語

本文基于蟻群優化K均值聚類算法，提出了一種滾軸故障預測方法。通過三層小波包分解得到了滾軸原始振動數據的特征向量，對特征向量進行歸一化，提高了故障預測模型的訓練速度。為避免陷入局部最優解，引入蟻群優化算法對傳統的K均值聚類算法進行了改進，在該算法中每只螞蟻根據先前螞蟻留下的信息素來尋找最佳解決方案，得到了最優的初始聚類中心。在西儲大學滾軸數據集上的實驗結果表明，相比基于傳統K均值聚類算法的滾軸故障預測，得到了更穩定和更準確的預測結果，準確率達到了97.76%。

面對實際生產中快速增長的海量滾軸振動數據，下一步將基于Spark平臺對蟻群優化K均值聚類算法進行并行化，以提高故障預測效率。