高斯過程回歸與參考點排序相結合的新WiFi室內定位系統

陶 冶，趙 龍

(1.北京航空航天大學自動化科學與電氣工程學院，北京 100191； 2.北京航空航天大學數字導航中心，北京 100191)

0 引言

隨著移動設備的發展，基于位置服務的需求越來越旺盛。在室外，可以通過衛星信號獲得載體的高精度定位結果，但由于室內環境的復雜性，使得衛星信號在室內無法定位。而基于WiFi的室內定位技術不需要安裝額外的硬件，使得該項技術成為常用的室內定位方案之一[1-2]。

基于WiFi的室內定位技術通常被分為兩類，一類是基于三邊測距的定位算法[3]，另一類是基于指紋的定位算法。但在非視距的情況下，三邊測距的定位精度不如指紋定位。因此，WiFi指紋定位技術被廣泛研究和應用。

通常WiFi指紋定位技術的流程分為兩步[4]，第一步：線下指紋庫的建立,該過程需要在線下采集不同點接收到的WiFi接入點(Access Point, AP)的信號強度，這些點又被叫作參考點；第二步：在線定位,該過程是將用戶上傳的測試數據與指紋庫中的信號強度進行匹配，選擇匹配度高的參考點進行加權平均定位。其定位步驟示意圖如圖1所示。

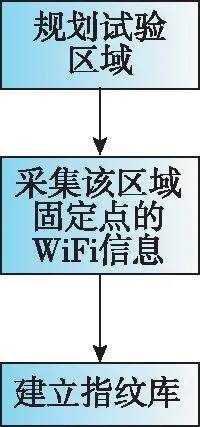
(a)離線采集 指紋庫

(b)采集測試 數據庫

(c)定位過程

WiFi指紋容易受到環境因素的影響，例如障礙物的移動、溫度、濕度、AP發射功率和位置變化等，因此指紋庫的時效性很低，需要不斷地更新指紋庫來保證定位精度[5]。此外，不同的指紋匹配算法也會影響定位精度[6]。

在指紋匹配算法方面，較為經典的算法有K近鄰(K-Nearest Neighbor，KNN)[7]和加權K近鄰(Weighted K-Nearest Neighbor，WKNN)算法[8]，但是這些算法都沒有考慮環境和指紋動態特性對定位精度的影響，因此往往定位精度較低。針對部分AP休眠、位置改變和AP在線信號突然探測不到等現象引起的定位誤差問題，DorFin[9]利用強回歸(Robust Regression)修正在線接收到的信號強度；LAAFU(Localization with Altered APs and Fingerprint Updating)[10]利用不同APs的信號強度子集篩除出變化的AP;自適應區域搜索(Adap-tive Area Search，AAS)[11]利用參考點排序算法削弱這些現象對于定位的影響。但是這些算法都沒有考慮信號本身所具有的動態變化問題。對于信號自身存在的動態變化問題，在采集指紋庫時，往往通過在每一個參考點采集多組數據進行平均來解決。但由于在線定位階段，用戶一般只在一個點停留1～2s，因此上傳的測試數據具有噪聲，無法很好地反映當前測試點的真實信號強度。

在指紋庫更新算法方面，基于Matern核的Zero_GPR[12]算法得到了廣泛的研究，但是該算法沒有考慮WiFi信號自身的傳播特性；DNCIPS[13]利用在固定節點放置設備，實時采集信號強度，并通過WiFi信號傳播擬合公式(LDPL模型)[13]和基于SE核的高斯過程回歸(Gaussian Process Regres-sion，GPR)提出了LDPL_GPR算法進行指紋庫更新，但是該算法需要在固定位置額外放置設備。

為了解決上述問題，本文提出了一種新的WiFi室內定位系統，該系統包括一個新的定位算法和指紋更新算法。新的定位算法改進了基礎參考點排序算法，同時考慮了測試信號本身的動態變化特性。該改進算法將處于同一范圍內的參考點排序視為與測試點具有相同的相似度，這是因為所獲取的測試信號強度受到了噪聲干擾，而這些噪聲使得參考點排序結果不穩定，所以采用模糊化的方法會更好地刻畫每一個參考點與測試點之間的信號強度相關性。指紋庫自更新算法考慮了WiFi傳播特性，利用其傳播模型模擬每一個點的信號強度，并結合GPR算法以逼近真實的信號強度。與DNCIPS[13]不同的是，該算法利用上傳的測試數據預測未知點的信號強度，而不需要在固定位置處放置設備來實時獲得信號強度，這使得新的指紋更新算法更加靈活，且該算法利用Matern核更好地刻畫了坐標點與相對應的信號強度之間的非線性關系。

為了驗證系統的有效性，在北京航空航天大學新主樓4層采集了真實數據，并與已有的算法進行了大量的對比實驗。實驗結果顯示，該系統可以很好地提高定位精度和指紋更新精度。

1 系統簡介

本文提出的WiFi室內定位系統的實現過程示意圖如圖2所示，主要包括在線定位和在線指紋自更新兩部分。

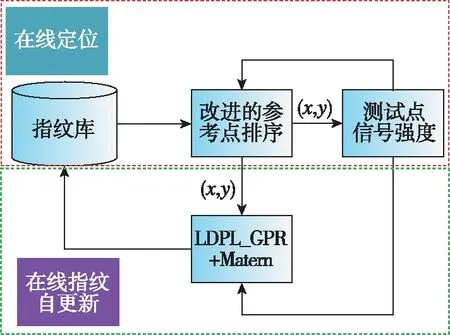
圖2 WiFi定位系統實現過程Fig.2 Implementation process of WiFi positioning system

在線定位時，將接收到的測試點信號強度與指紋庫進行對比，通過改進的參考點排序算法進行匹配得到定位結果(x,y)。由于改進的參考點排序算法可以提供較高的定位精度，因此在線進行指紋自更新時，LDPL_GPR+Matern算法將定位結果(x,y)作為真實位置，并利用對應接收到的信號強度去預測其余未知點的信號強度，從而實現了指紋庫的在線自更新。

2 新定位系統的理論和算法

本節在簡單介紹參考點排序算法的基礎上，重點介紹了改進的參考點排序定位算法和指紋更新算法。

2.1 參考點排序

對于同一AP，首先計算參考點與測試點接收到的信號強度差的絕對值，其計算公式為[11]

errorji=|sij-tj|

(1)

式中，errorji表示第i個參考點接收到的第j個AP的信號強度與測試點接收到的第j個AP的信號強度之間差的絕對值；sij表示第i個參考點接收到的第j個AP的信號強度；tj表示測試點在線接收到的第j個AP的信號強度。

然后，將信號強度差的絕對值轉換為從1～m的排序，其轉換公式為[11]

rank(RPij)=find(errorji=sort(errorj))

(2)

式中，rank(RPij)表示第i個參考點接收到的第j個AP的信號強度與測試點接收到的第j個AP的信號強度之間的差在所有參考點與測試點信號強度差中的排序；errorj=[errorj1,errorj2,…,errorjm]；sort(*)表示對向量由小到大進行排序；find(A==B)表示元素A在向量B中的索引；m表示參考點的數量。

同理，逐一計算參考點在每一個AP下的排序，然后計算每一個參考點在所有AP下的排序平均值，并將其作為該參考點的最終排序。其第i個參考點的綜合排序計算公式為[11]

(3)

式中，n表示AP的數量。

最后，根據每一個參考點的綜合排序，選擇排名靠前的k個參考點進行加權平均定位，其對應權重可表示為[11]

(4)

于是，最終的定位結果可表示為

(5)

式中，loci=(xi,yi)為所選取的第i個參考點的坐標；loct為最終預測的測試點的位置結果。

2.2 改進的參考點排序算法

圖3所示為1min內在同一點連續接收同一AP的信號強度值的統計直方圖。從圖3中可以看出，信號強度會隨著時間的變化而變化，因此直接將絕對差值轉換為排序，忽略了信號強度動態變化帶來的誤差，這會導致系統的定位精度降低。

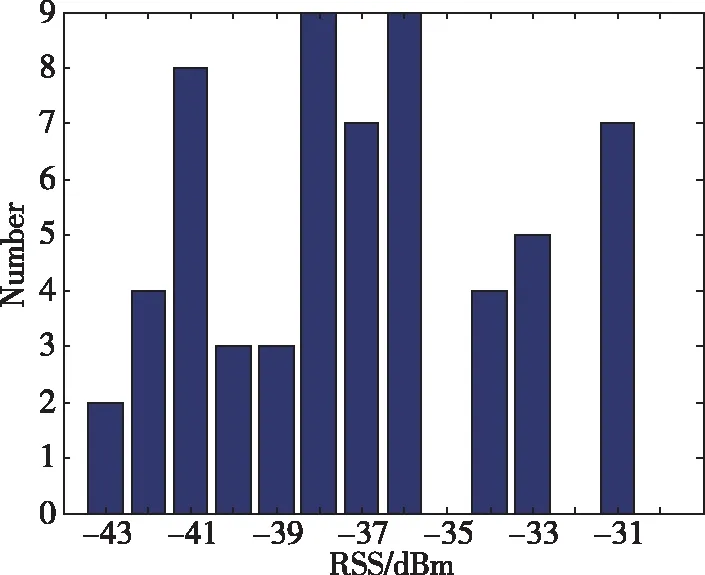
圖3 1min收集到的定點信號強度分布Fig.3 Distribution of RSS collected at a fixed point in one minute

為解決該問題，本文提出了一種改進的算法，該算法采用模糊的思想，將處在同一個范圍內的排序結果視為相同的排序，其數學表達式為

(6)

式中，β為長度參數，控制排名的范圍。

由于參考點與測試點位置越接近，其對應的參考點會在更多的AP下具有更好的排序。基于這一事實，本文提出的改進算法重新定義了參考點的綜合排序計算方法，其中第i個參考點的綜合排序計算公式可表示為

(7)

于是權重表示為

(8)

2.3 指紋更新算法

Zero_GPR[12，14]是一種適合非線性回歸問題的無參數模型，可通過訓練數據的輸入限制先驗分布實現貝葉斯框架下的后驗分布狀態預測，輸出預測的均值和方差，預測結果具備不確定表達能力。其回歸模型可表示為

s=f(w)+η

(9)

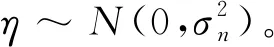
假設有m個訓練數據，其輸入為w，則觀測值s的先驗分布可表示為

f(w)～GP(0,k(wi,wj))

(10)

式中，核函數k(wi,wj)一般表示為SE核函數，其表達式為

(11)

且當wi=wj時，有

(12)

式中，σf表示協方差因子；l表示長度參數。

對于未知點w*處信號強度的預測值s*和觀測值s之間服從聯合分布

(13)

式中

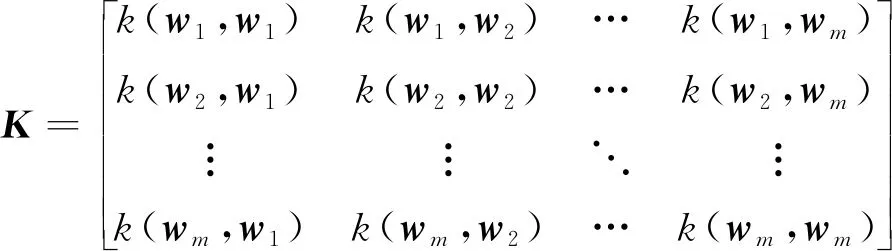
預測值的后驗分布模型為

(14)

因此，未知點處信號強度的預測均值為

s*=K*K-1s

(15)

在文獻[12]中發現，基于高斯過程回歸的GPR模型，使用Matern核對信號強度的預測效果要優于使用SE核的預測效果，Matern核的表達式為

(16)

而單獨使用Zero_GPR預測未知點的信號強度時，在預測遠離訓練點的未知點的信號強度的預測均值在0附近，這顯然不符合WiFi信號強度的傳播特性。本文結合WiFi傳播模型，對基于Matern核的Zero_GPR算法進行了改進，并提出了LDP_GPR+Matern預測模型。WiFi傳播模型可表示為LDPL模型[13]，其表達式為

(17)

式中，wAP=[xAP,yAP]；C表示參考點距離AP為1m時接收到的信號強度；α為衰減系數。

對于w*接收到第j個AP的信號強度的預測表達式為

(18)

本文利用最小殘差思想求解Cj、α、xAPj、yAPj，其目標函數表達式為

(19)

本文利用最大似然估計求解LDPL_GPR+Matern算法的最優參數l、σn，其目標函數表達式為

(20)

式中，z=s-m(w)。

在此基礎上，本文利用煙花算法[15]進行尋優求解以獲得所求參數。

3 實驗驗證與分析

3.1 實驗環境與測試條件

為了驗證系統中算法的有效性，在北京航空航天大學新主樓4層采集數據，并進行了實驗驗證。圖4所示為實驗環境的布局，長為70m，寬為15m。圖4中，紅色圓圈表示線下建庫時的指紋參考點，一共125個，每一個參考點的采樣時間為60s；綠色方框點表示在線測試點，一共79個，實驗過程中每一個測試點的采樣時間為1～2s。為了測試算法在陌生環境下的工作性能，沒有對AP的相關信息(位置、發射功率等)進行提前調研，所探測到的AP的信息均是未知的，在這樣的環境下進行實驗測試更能說明算法的普適性。本文利用熵信息[16]篩選出50個區分度大的AP進行定位，以減少在線定位運算時間。

圖4 實驗區域分布圖Fig.4 Layout of experimental area

3.2 定位實驗結果及分析

為驗證定位算法的有效性，本次實驗利用參考點預測79個測試點的位置，且實驗時設置了不同的β值進行了多次定位實驗，最終取平均結果代表該改進排序算法的最終定位精度，β=(0.04,0.08,0.12,0.16,0.20,0.24,0.28,0.32)。將所提算法的定位結果與KNN、WKNN和已有的參考點排序算法進行對比分析。文中KNN與WKNN算法使用測試點與參考點之間信號強度的歐式距離篩選與測試點相似的參考點，且將歐氏距離的倒數作為WKNN算法中相似參考點的權重。當k=5時，不同算法的累計誤差概率分布(Cumulative Distribu-tion Function，CDF)如圖5所示。

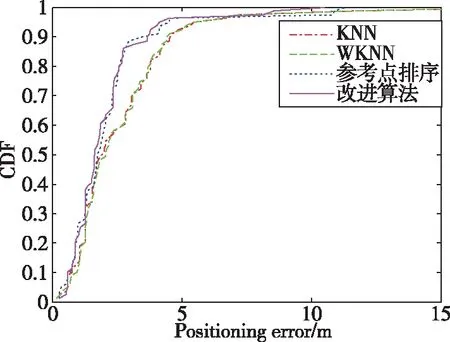
圖5 不同算法的累計誤差概率分布圖Fig.5 Cumulative distributions of positioning error of different algorithms

從圖5中可以看出，基于參考點排序和改進的參考點排序算法的定位結果曲線幾乎都位于KNN和WKNN定位曲線的上方，這說明基于參考點排序算法是有效的，而且改進算法的定位結果相對于參考點排序算法在均值誤差和標準差方面均有所提升。為了進一步量化所提算法的優越性，對定位結果進行了相應的統計，統計結果如表1所示。

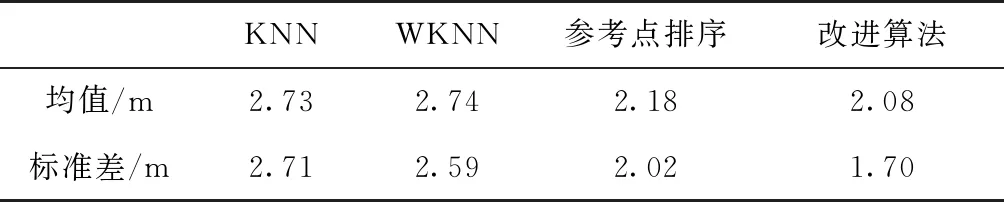
表1 不同算法的定位結果統計

為進一步說明改進算法的優勢，本次實驗統計了k取不同值時不同算法的定位精度，其結果分別如圖6和表2所示。其中，圖6所示為k取不同值時不同算法的均值誤差；表2所示為k取不同值時不同算法的均值誤差和標準差。從圖6和表2中可以看出，在均值誤差方面，改進的參考點排序算法相對于KNN、WKNN和參考點排序算法分別提升了25.52%、25.52%和4.05%；在標準差方面，改進的算法相對于KNN、WKNN和參考點排序算法分別提升了33.86%、30.86%和8.70%。

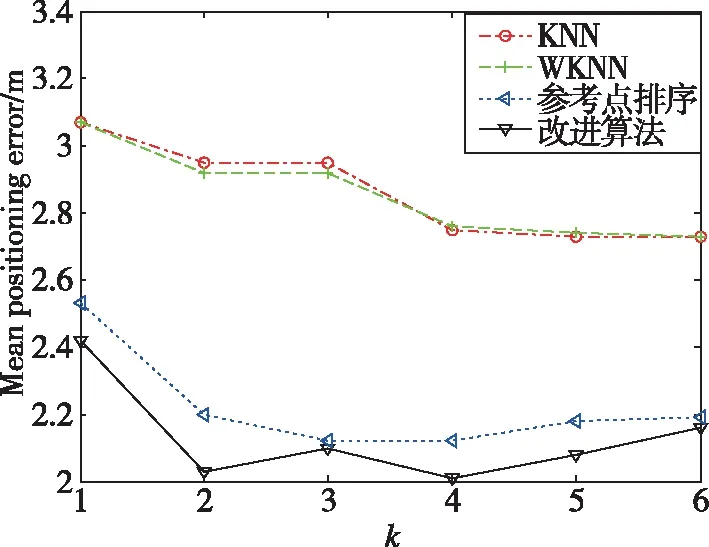
圖6 不同算法下的平均定位誤差Fig.6 Mean positioning errors with different algorithms

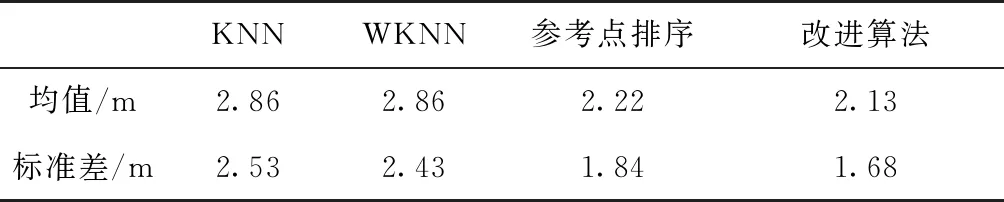
表2 不同算法的定位結果統計

3.3 指紋更新實驗結果及分析

為了驗證指紋更新算法的有效性，本次實驗利用參考點預測40個測試點的位置，在定位的基礎上，利用40個點的信息和指紋更新算法預測剩下39個測試點的信號強度，并與真實信號強度進行對比，得到信號強度的預測誤差。本次實驗將LDPL_GPR+Matern的預測結果分別與ZERO_GPR+SE和ZERO_GPR+Matern進行對比，不同算法預測結果的均值誤差和標準差如表3所示。

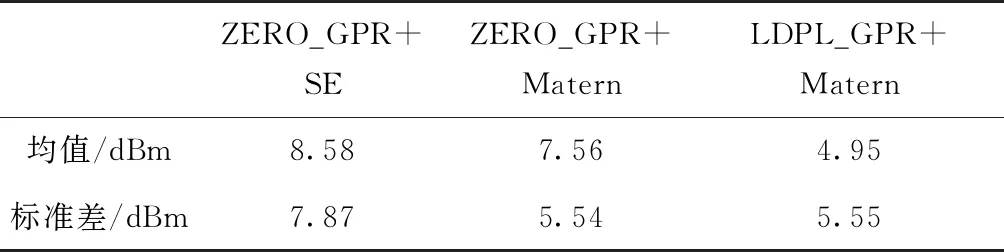
表3 不同算法的信號強度預測誤差統計

從表3中可以看出，ZERO_GPR+Matern算法的均值誤差和標準差比ZERO_GPR+SE算法的都小，這說明Matern核相較于SE核確實更適用于預測WiFi信號的信號強度。與ZERO_GPR+Matern相比，LDPL_GPR+Matern的標準差幾乎保持不變的同時，均值誤差降低了34.52%，這說明結合LDPL模型和GPR模型可以有效提高對于未知點信號強度的預測精度。

4 結論

本文提出了一種新的WiFi指紋定位系統，該系統可以長期封閉式運行，且保持較高的定位精度。該系統在定位方面，改進了參考點排序算法，以提升定位精度；在指紋更新方面，利用LDPL模型和基于Matern核的GPR算法在線進行指紋自更新，以避免線下指紋庫更新的繁瑣。根據相關分析及實驗結果表明：

1)所提出的基于模糊思想的參考點排序算法，考慮了WiFi自身的動態特性。相較于傳統的定位算法(KNN和WKNN)，該算法能夠提升25%以上的定位精度。

2)所提出的指紋更新算法利用Matern核更好地刻畫了參考點坐標和RSS之間的非線性關系，且使用LDPL模型克服了Zero-GPR的零均值問題。相較于已有的指紋更新算法，該算法能夠提升34%以上的指紋還原精度。

在未來的工作中，將探索不同的長度參數β對于定位結果的影響，以及嘗試尋找合適的參數自適應確定方法。