基于響應面法的導向篩管結構尺寸優化

王 晶 羅 敏 林志強 徐亭亭

（東北石油大學a.數學與統計學院；b.機械科學與工程學院）

超短半徑徑向側鉆水平井技術在挖潛剩余油、降低鉆井成本及提高原油產量等方面有著不可忽視的作用［1～4］。 目前，超短水平井技術主要采用的鉆井方法可分為高壓射流鉆井［5，6］和柔性鉆具鉆井［7，8］兩種。

國內外學者對柔性鉆具的研究做了相關工作。 蘇義腦和趙俊平在二維井身條件下建立了鉸接式柔性鉆具的力學模型，并進行了分析，得到了影響鉆頭側向力的主要參數［9］。 趙俊平等將鉸看作平面鉸，通過靜力學分析，確定了井底鉆壓與大鉤載荷之間的關系以及任一鉸鏈處的受力情況［10］。 Liu H等對柔性鉆桿進行了力學分析，得到了柔性鉆桿所能承受的極限載荷［11］。 帥健等采用凝聚自由度的方法推導出含鉸接梁單元和桿系結構的剛度矩陣和載荷列陣［12，13］。 Gourley G對設計的柔性鉆具開展了實驗研究，并對其開窗側鉆能力進行了評價，結果表明采用柔性鉆具鉆井可提高采收率［14］。

雖然學者們對柔性鉆具開展了相關的研究工作，但是大都針對鉸接柔性鉆桿，而對于單側開槽的導向篩管的研究則較少。 為此，筆者根據導向篩管的工作狀態，采用有限單元法，建立導向篩管材料和接觸雙重非線性有限元模型，采用響應面法進行結構優化設計，并對優化后的導向篩管進行力學分析。

1 導向篩管有限元模型

1.1 物理模型

導向篩管是柔性鉆具的關鍵部件，在超短半徑水平井鉆井中，導向篩管主要傳遞軸向力。 導向篩管結構如圖1 所示， 單節篩管長度l1為100mm， 豎縫長度l為58mm， 篩管豎縫寬度b為4mm，兩豎縫中心線的夾角θ為70°，篩管橫縫寬度h為4mm，外徑D為110mm，內徑d為95mm，d′為截面形心到y軸的距離，y1為開縫截面上距離形心的最大距離，它與豎縫夾角有關。

1.2 有限元模型

導向篩管的材料為35CrMo， 彈性模量為211GPa，泊松比為0.3，屈服極限為835MPa，強度極限為980MPa。 以單節導向篩管為研究對象，采用有限單元法將導向篩管離散為實體單元，將導向篩管應力-應變關系簡化為多線性等向強化模型。 當應力未達到屈服極限σs時，應力-應變關系符合彈性關系；當應力值超過屈服極限σs時，則為線性強化關系。 邊界條件為：導向篩管下端全固定，上端加40kN的軸向力Fy（鉆井時承受的開窗點軸向力），橫縫之間為接觸摩擦邊界，摩擦系數取0.3。 導向篩管的力學模型及有限元模型如圖2 所示。

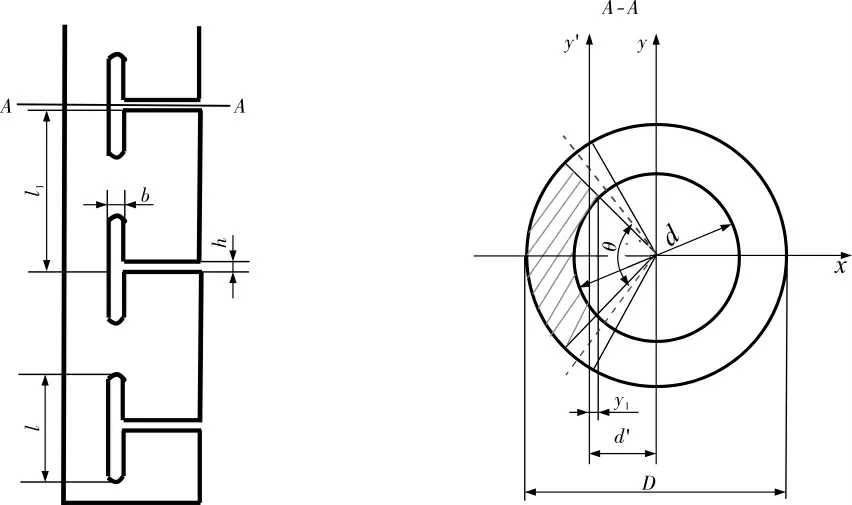
圖1 導向篩管結構示意圖

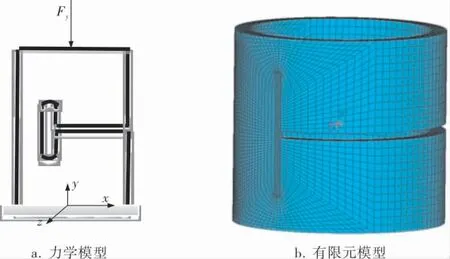
圖2 導向篩管的力學模型及有限元模型

導向篩管應力σ與應變ε之間的關系是非線性的，物理方程可寫為：

由于橫縫寬度較小，因此導向篩管的變形為小變形，應力表達的平衡方程仍是線性的，幾何關系依然成立，但是以節點位移列陣表示的平衡方程則是非線性的，可表示為：

其中，K（δ）為導向篩管的彈塑性剛度矩陣，δ、F分別為節點位移列陣和節點力列陣。

為了分析導向篩管橫縫上、 下表面間的接觸，分別在上、下表面創建接觸單元和目標單元，采用增廣拉格朗日法計算接觸力。 將實體單元與接觸單元相結合，可以得到分析導向篩管材料和接觸雙重非線性的靜力學總體平衡方程：

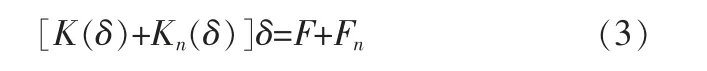
其中，Kn（δ）為接觸剛度矩陣；Fn為接觸力列陣，是節點位移的函數。

上述方程均采用修正的牛頓辛普森法進行求解。

2 導向篩管靜力學分析

通過對導向篩管的靜力學分析，得到剖切過后的導向篩管等效應力云圖如圖3所示。 可以看出，單節導向篩管的最大等效應力為941.81MPa，位于豎縫兩端。

為了使導向篩管的變形在彈性范圍內，需以導向篩管危險部位為評價標準，即導向篩管背部不能出現塑性應變，所以筆者在導向篩管內部受壓的危險截面設置一條路徑，以這條路徑上的最大應力為響應參數，得到該路徑上的最大等效應力為703.11MPa，如圖4所示。

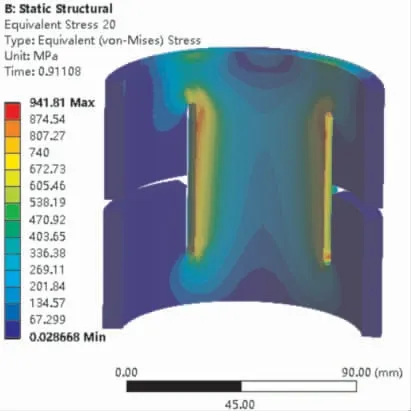
圖3 剖切過后的導向篩管等效應力云圖

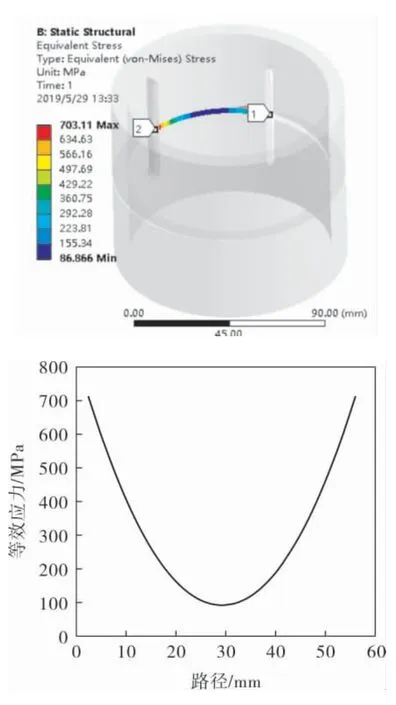
圖4 自定義路徑上的等效應力

導向篩管轉過的弧長如圖5所示， 最大值為1.672 6mm。 為了提高導向篩管的柔度，使導向篩管能夠更好地實現轉向能力，需要導向篩管具有更大的彎曲量，所以以導向篩管的弧長為響應參數， 把危險截面上的最大等效應力作為約束函數，在后續的響應面優化分析中求解出符合強度條件的導向篩管優化模型尺寸。

3 優化模型

3.1 目標函數與設計變量

以導向篩管的轉角為響應參數，把危險截面上的最大等效應力作為約束函數，求解出符合強度條件的導向篩管優化模型尺寸。 該優化問題可描述為：

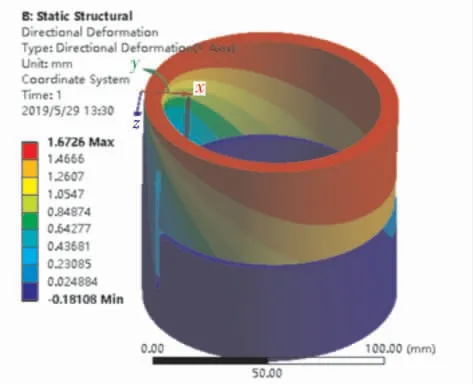
圖5 導向篩管轉過的弧長

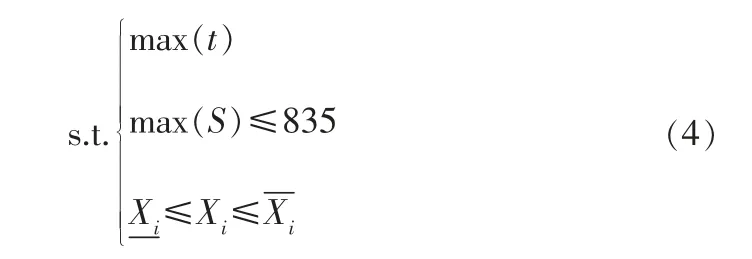
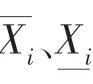
為了給出設計變量的取值范圍，根據幾何關系和強度條件進行計算。 隨著豎縫夾角的增加，截面面積隨之增加， 距離形心的最大距離增大，慣性矩增加，最大應力和彎矩增加，安全系數降低。

當導向篩管整體結構達到井眼曲率半徑ρ1時，強度條件為：

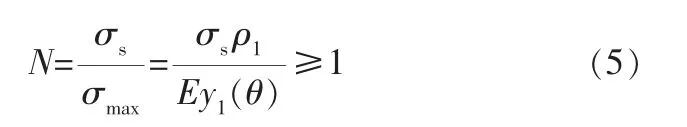
其中，N為安全系數，σmax為導向篩管等效應力的最大值，E為材料的彈性模量。

導向篩管達到井眼曲率半徑ρ1時其初彎矩M的計算式為：

其中，Iy′為開縫截面對形心軸y′的慣性矩。

根據式（5）、（6）可以得出，井眼曲率為2.8m時導向篩管中心夾角不小于50°，所以在優化過程中給出夾角的范圍為50～70°。

內壁最大應力強度條件為：

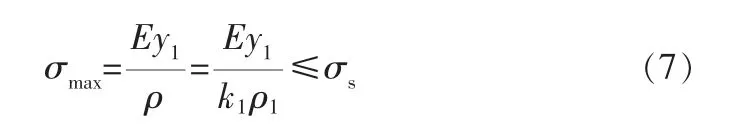
其中，ρ為彎曲導向篩管的曲率半徑，k1為單節導向篩管豎縫的長度與單節長度的比值，k1min為k1的最小值。

豎縫長度l的計算式為：

由幾何關系可得豎縫寬度最小值bmin為：

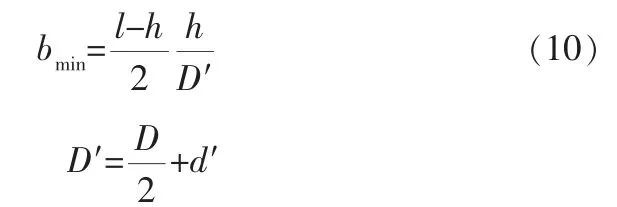
通過計算可以得出， 豎縫長度的范圍為40～70mm，豎縫寬度的范圍為2～8mm。 考慮到橫縫寬度h太小會造成加工不便，而h太大又不利于密封，綜合考慮后給出橫縫寬度的范圍為2.0～7.5mm。

3.2 響應面法

二階響應面模型為：

其中，xi是m維優化設計變量的第i階分量，β0、βi、βii、βij是多項式的待定系數。

選取n個樣本點， 采用最小二乘法對多項式的待定系數進行確定，即：

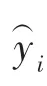
3.3 優化結果

通過優化分析，得到了導向篩管結構尺寸的優化結果（表1）。

表1 導向篩管尺寸優化結果

優化后，導向篩管強度滿足要求，其危險截面上的最大等效應力（672.99MPa）相比原結構的（703.11MPa）有所降低。

4 結論

4.1 以單節導向篩管為研究對象，根據導向篩管各結構尺寸參數，考慮導向篩管材料非線性及導向篩管橫縫之間的接觸非線性， 采用實體單元，建立了單節導向篩管的有限元模型，給出了數值求解方法。

4.2 通過靜力學分析，得到了導向篩管應力分布狀態及危險截面位置，應力較大位置出現在豎縫內壁邊緣。

4.3 采用響應面法對導向篩管的主要尺寸進行了優化，優化后：兩豎縫中心線的夾角為62°，豎縫長度40mm，豎縫寬度4mm，橫縫寬度7.5mm。優化后的導向篩管強度滿足要求， 整體應力水平與原結構相比有所降低， 轉過的弧長增加了90.8%。