音圈快速反射鏡的完全跟蹤控制

王福超，王昱棠*，田大鵬

(1.中國科學院 航空光學成像與測量重點實驗室，吉林 長春 130033；2.中國科學院 長春光學精密機械與物理研究所，吉林 長春 130033)

1 引 言

航空、航天成像裝備及其他高端光電儀器對成像距離提出了更高的要求，而隨著探測距離的不斷提升，成像設備的穩定精度要求也越來越高。傳統控制視軸指向的機械框架慣量大、剛度低，并且受到設計約束和干擾力矩等因素的影響，系統控制精度以及控制帶寬難以提升。快速反射鏡(Fast Steering Mirror，FSM)具有體積小、質量輕、結構緊湊、響應快、精度高等優點[1-2]，廣泛應用于空間光通信、像移補償以及高精度跟蹤瞄準等領域[3-5]。通過在成像光路中加入FSM并采用復合軸控制方式補償視軸晃動，有效提高了視軸穩定精度和系統的成像質量[6-9]。

FSM按照驅動方式不同主要分為壓電陶瓷驅動和音圈電機驅動[10]。壓電陶瓷驅動方式具有力矩輸出大、響應帶寬高的優點，但這種驅動方式下FSM的行程較小，并且驅動電路相對復雜。同時，壓電陶瓷存在遲滯、蠕變等非線性特性，需要通過算法進行補償，增加了工程應用的復雜度。與之相比，基于音圈電機驅動的FSM(以下簡稱音圈FSM)具有行程大、動態特性好、結構簡單、環境適應性強等特點，工程應用更為廣泛。

國內外相關機構已設計并制造多種音圈FSM。美國Ball Aerospace公司設計的多尺寸音圈FSM行程可達±50 mrad，工作帶寬可達250～1 000 Hz。美國OIM公司生產的音圈FSM角度為±27 mrad，工作帶寬大于500 Hz。國內對于音圈FSM的研制起步較晚，但發展較快。國防科技大學設計的音圈FSM的轉動范圍為±5 mrad，閉環控制帶寬為360 Hz[11]，長春光機所研制的一種音圈FSM的工作帶寬為213 Hz[12]。但是，上述帶寬指標均只考慮幅值下降，而未對相位滯后進行衡量。實際上，相位滯后會直接影響FSM的實際應用效果。在音圈FSM補償系統視軸穩定時，較大的相位滯后會導致反射鏡的實際運動與指令之間偏差的絕對值較大，直接影響系統視軸穩定精度。隨著光學系統口徑、焦距的提高，這一問題也愈發凸顯，如何在保證音圈快速反射鏡工作帶寬的前提下減少系統的相位滯后，已成為提升音圈FSM性能的關鍵問題之一。

實際工程中采用的FSM控制方法仍然以傳統的PID控制以及超前滯后校正方法為主。然而，傳統控制方法不僅魯棒性較差，其閉環系統存在明顯的相位滯后現象。為了解決上述問題，文獻[13]提出了一種基于零相差軌跡控制(Zero Phase Error Tracking Controller，ZPETC)的音圈FSM控制方法，提高了系統的響應速度。但是，該方法需要獲取指令超前信息，并且為了避免不穩定零極點對消需采用近似逆模型，因此限制了系統頻帶的拓寬，理論上存在跟蹤的幅值誤差。

實際上，為了保證FSM的控制性能，其控制器的控制周期較短，而外部控制計算機發送給FSM控制器的指令周期往往大于反射鏡的控制周期，即實際音圈FSM系統存在多速率采樣問題。常見的思路是通過插補的方式解決控制周期與指令周期不同的多速率采樣問題，但這樣不能很好地利用這種采樣速率的差異特性。文獻[14]利用多速率采樣特性，不對指令進行插補，通過對前饋的巧妙設計從理論上實現了控制系統對指令的完全跟蹤控制(Perfect Tracking Controller，PTC)，其核心思想是把單輸入單輸出(Single Input Single Output，SISO)的被控對象描述為多輸入多輸出(Multiple-Input-Multiple-Output，MIMO)系統，從而構造出對象狀態到輸入控制量之間非奇異的傳遞函數矩陣。利用該模型求解穩定的逆控制即可實現高動態跟蹤控制，在硬盤驅動器、單相逆變器等領域得到較廣泛的應用[15-16]。國內對該方法的研究成果較少[17-18]。近年來，基于完全跟蹤的光電跟蹤轉臺控制及光刻機直線電機控制的應用結果證實它在提高系統動態性能方面的有效性[19-20]。那么，針對音圈FSM對指令的寬頻帶跟隨要求和現有控制方法性能的限制問題，可以基于完全跟蹤控制的思想給出更適合工程應用的控制器設計。

本文以音圈FSM為研究對象，構建了多速率采樣系統并給出它適用的完全跟蹤控制方法。針對魯棒性和控制帶寬的高要求，采用離散滑模內回路補償控制器和多速率采樣下前饋控制器相結合，提出了音圈FSM的完全跟蹤控制方法。該方法有效提高了控制性能，解決了傳統方法對閉環帶寬的限制問題。

2 控制對象數學建模

音圈電機驅動FSM的物理結構如圖1所示。反射鏡通過柔性鉸鏈與基座相連，通過控制反射鏡兩端的音圈電機伸縮實現反射鏡的旋轉運動。

圖1 音圈快速反射鏡物理結構Fig.1 Schematic diagram of VCM fast steering mirror

音圈FSM采用柔性鉸鏈而非軸承結構作為基座與鏡面的連接部件，柔性鉸鏈的彈性力矩與反射鏡的轉動角度成正比。

根據音圈FSM物理特性建立系統控制模型的方框圖，如圖2所示。

圖2 FSM系統控制模型的方框圖Fig.2 Block diagram of FSM system control model

圖中，Ra為線圈電阻，La為線圈電感，i為線圈中的電流，Ke為反電動勢系數，θm為電機轉角，Tm為電機作用在反射鏡上的力矩，Kt為電磁力常數，Jm為電機轉動慣量，Bm為電機端黏性阻尼系數，Ks為柔性鉸鏈的彈性系數。

根據圖2求得被控對象的傳遞函數為：

(1)

實際系統中電機的電感非常小，可以忽略不計，因此式(1)可以簡化成：

(2)

取狀態變量x(t)=[x1(t)，x2(t)]T，x1(t)與x2(t)分別代表t時刻音圈快速反射鏡的位置和速度。將上述傳遞函數轉換成狀態空間模型，如式(3)所示：

(3)

其中：

(4)

(5)

(6)

實際控制系統是在嵌入式處理器上以離散方式實現的，因此將公式(3)按采樣周期Ts進行離散化得到離散狀態方程：

(7)

其中：

(8)

控制器的設計將針對上述離散SISO系統開展。

3 控制器設計

本節利用系統的多速率采樣特性，設計音圈FSM完全跟蹤控制器(PTC)。控制器由基于短采樣周期的內回路補償控制器和基于長指令周期的前饋控制器組成。

3.1 多速率采樣系統

為了保證音圈FSM的控制性能，其控制周期一般較短，而通常外部控制計算機發送給FSM控制器的指令周期要長于控制周期。因此，音圈FSM控制系統由長指令周期與短控制周期構成。指令周期Tr作為長周期部分，控制周期Tu和反饋采樣周期Ty作為短采樣周期部分[21-22]存在如式(9)所示的關系：

Tr>Tu=Ty=Ts.

(9)

指令周期與控制周期的不一致直接影響最終的控制性能。為了解決這一問題，通常采用插值的方式計算出iTr時刻與(i+1)Tr時刻之間的指令替代外部控制計算機的控制指令。為了更好地利用多速率采樣特性，對長周期采樣部分合理設計前饋，實現完全跟蹤；對短周期部分設計合理的反饋以提高魯棒性。兩者結合實現對FSM的控制。

圖3 多速率采樣系統完全跟蹤控制器結構Fig.3 Control structure of PTC with multi-rate sampling

圖3為多速率采樣系統完全跟蹤控制器結構圖。其中，CM(z)為前饋控制器，CM(z)為MIMO環節，CR(zs)為反饋控制器，CM(z)與CR(zs)共同作用，最終實現完全跟蹤功能。L(t)為提升器，它按照短采樣周期Ts依次輸出其輸入向量u[i]中的每個元素uk[i]，L(t)為MISO環節。根據式(2)可知FSM為二階系統，因此可得：

u[i]=[u1[i]，u2[i]]T，

(10)

(11)

其中：Pc(s)為連續的被控對象，SM為采樣器，HM為保持器。

3.2 長周期控制器設計

設定指令周期與短采樣周期的關系為Tr=nTs，其中n為被控對象狀態變量的個數，即被控對象的階數。根據式(2)可知n=2，將按短采樣周期Ts進行離散化得到的離散狀態方程(7)進行轉換，將短周期采樣的SISO系統轉換為長周期采樣的MIMO系統：

(12)

其中：

y[i]=[y1[i]，y2[i]]T，

(13)

(14)

由式(12)可以得到：

(I-z-1A)x[i+1]=Bu[i]，

(15)

當u[i]=B-1(I-z-1A)xd[i+1]時，就可以實現被控系統的狀態對期望狀態的完全跟蹤。其中，xd[i+1]是下一時刻系統的期望狀態，即：

x[i]=xd[i].

這樣就得到前饋控制器：

CM(z)=B-1(I-z-1A)-CR(z)z-1C=
CM0(z)-CR(z)z-1C.

(17)

3.3 短周期控制器設計

考慮實際被控對象存在模型建模誤差、外界干擾等因素，可以將圖3中的短周期采樣控制部分變換為圖4所示的結構，通過加入對模型跟蹤的反饋控制保證控制系統對干擾等不確定因素的魯棒性。

考慮干擾后式(7)可以改寫為如下形式：

(18)

其中dex(k)為等效干擾值。

圖4 短周期采樣控制結構的變形Fig.4 Structure deformation of short-cycle control

為了使系統具有更快的響應速度、更高的控制精度以及更強的抗干擾性能，在進行反饋控制器設計時，圖4中的控制器CR(zs)可以采用離散滑模變結構控制方法[23]。

設系統的輸入控制指令為r(k)，其對應的變化率為dr(k)，取R(k)=[r(k)，dr(k)]T；采用線性外推的方法預測r(k+1)以及dr(k+1)，即：

(19)

令滑模控制的切換函數為：

s(k)=Ce[R(k)-x(k)]，

(20)

其中Ce=[c1]。則：

s(k+1)=Ce[R(k+1)-x(k+1)]=
Ce[R(k+1)-Asx(k)-bsu(k)-bsdex(k)].

(21)

得到控制率為：

u(k)=(Cebs)-1[CeR(k+1)-
CeAsx(k)-s(k+1)]，

(22)

則基于指數趨近率的離散趨近率為：

s(k+1)=s(k)+Ts(-εsgn(s(k))-
qs(k))-Cebsdex(k).

(23)

將式(23)帶入式(22)，得到離散控制率：

u(k)=(Cebs)-1[CeR(k+1)-
CeAsx(k)-s(k)-ds(k)]，

(24)

其中ds(k)=-Tsεsgn(s(k))-qTss(k)。

基于趨近率的離散滑模變結構控制器，可以通過調節控制參數q，ε，c實現控制器的設計。其中q為趨近速度參數，主要影響切換函數的動態過度過程，調節該參數可以改變系統向滑模面的趨近速度。ε為符號函數的增益參數，影響系統克服參數攝動以及外界干擾能力，該參數越大系統的抗干擾能力越強，但是過大的增益會導致系統抖振。c為滑模面參數，影響系統的調節時間，c越大系統的快速性越好，但是過大的滑模面參數會導致系統的抖動。

選取李亞普諾夫函數：

(25)

當公式(25)滿足時，短周期控制系統能夠穩定。

(26)

根據李亞普諾夫穩定性定理，s(k)=0全局漸近穩定，離散滑模的存在和到達性條件為：

[s(k+1)-s(k)]sgn(s(k))<0，
[s(k+1)+s(k)]sgn(s(k))>0.

(27)

由式(23)有：

[s(k+1)-s(k)]sgn(s(k))=
[-Tsεsgn(s(k))-qTss(k)-Cebsdex(k)]sgn(s(k)).

(28)

(29)

[s(k+1)-s(k)]sgn(s(k))<0.

(30)

(31)

由此可見，當滿足以上條件時，所設計的滑模控制率滿足式(27)所示的離散滑模的存在和到達性條件，所設計的控制系統是穩定的。

4 實驗與結果

4.1 實驗設置

本文以音圈FSM為對象進行了實驗驗證，自研的音圈FSM如圖5所示。音圈FSM口徑為45 mm×35 mm，角度行程為±3 600″，反射鏡控制系統以TMS320F28335數字信號處理器為核心，控制算法通過C語言進行編寫。控制信號通過并行總線上的16位D/A轉換器與功率放大器相連，鏡面偏轉角度的反饋信號通過A/D轉換器進行采集，系統的采樣與控制周期Ts=0.1 ms。

圖5 音圈快速反射鏡系統Fig.5 VCM fast steering mirror system

利用偽隨機噪聲和頻譜分析的方法對控制對象傳遞函數進行辨識。圖6為音圈FSM的開環系統模型。

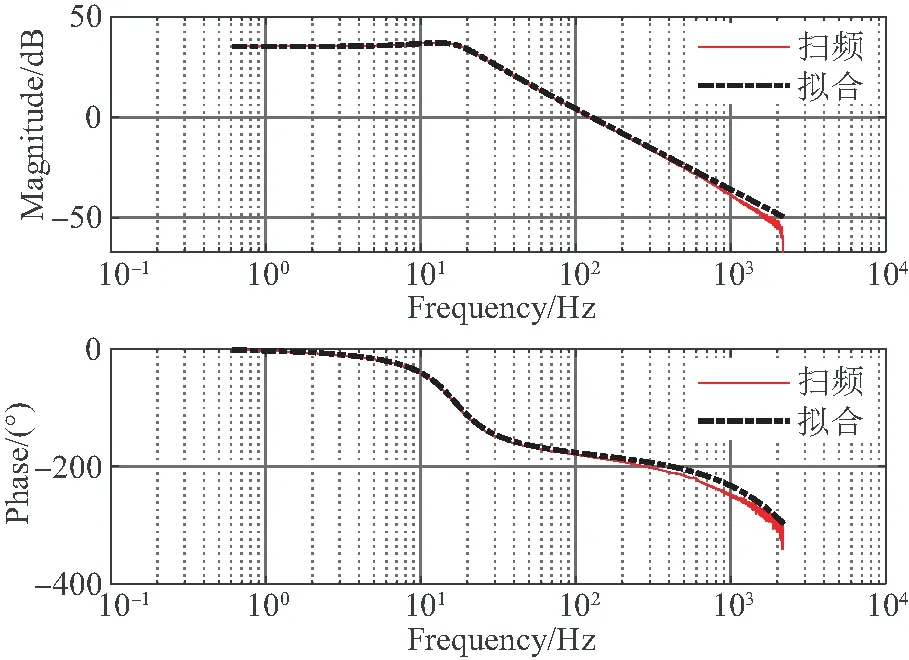
圖6 音圈快速反射鏡開環系統模型Fig.6 Identification results of VCM FSM

通過掃頻可以得到系統的模型參數如表1所示：

表1 音圈快速反射鏡參數

通過上述參數擬合得到系統傳遞函數：

(32)

針對式(32)所示的被控對象進行長周期控制器以及內回路補償控制器設計。首先，采用Tr=0.2 ms按照式(14)設計長周期控制器，控制器具體參數如式(34)、式(35)所示：

CM0(z)=B-1(I-z-1A)，

(33)

(34)

(35)

然后，采用Ts=0.1 ms對式(32)所示的被控對象按照式(8)進行離散化得到被控對象的狀態空間表達式：

(36)

(37)

根據上述狀態空間表達式，針對圖 4中的內回路補償控制器CR(zs)，采用累試法進行控制器設計，設計結果如下：

u(k)=(Cebs)-1[CeR(k+1)-CeAsx(k)-s(k)+
Tsεsgn(s(k))+qTss(k)]，

(38)

(39)

q=2 980.335 6，ε=1 845.537.

(40)

最后進行實驗驗證，對本文所設計的PTC控制器進行性能測試，分別對比傳統PID控制、基于ZPETC和本文提出的PTC方法的實際控制效果。

4.1.1 靜態定位精度測試

在靜態定位精度測試中，通過對比3種控制器的穩態誤差以及位置波動的峰峰值，衡量控制器的控制性能。

4.1.2 動態性能測試

在快速反射鏡動態性能測試實驗中，分別對比3種控制器的階躍響應曲線和正弦跟蹤曲線，通過實驗結果衡量控制器性能。

4.1.3 系統帶寬測試

通過正弦掃頻測試對3中控制器的閉環控制帶寬進行測試。

4.2 實驗結果

4.2.1 靜態定位精度測試

音圈FSM的靜態定位精度是衡量反射鏡性能的一項重要指標，直接影響光電成像設備的成像質量。

系統輸入360″的恒值控制信號。從實驗結果可以看出采用PID控制方法系統存在0.3%的穩態誤差，反射鏡的位置波動峰峰值為2.16″；采用ZPETC控制方法系統存在1.5%的穩態誤差，反射鏡的位置波動峰峰值為1.08″；采用PTC控制方法系統的穩態誤差為0.05%，反射鏡的位置波動峰峰值為1.08″。

從實驗結果中可以看出，采用PTC控制方法相對于傳統的PID控制方法，系統的位置穩態誤差由0.3%減小到0.05%；相對于ZPETC控制方法，系統階躍響應的調節時間縮短50%，系統的位置穩態誤差由1.5%減小到0.05%，系統精度得到明顯提升。

圖7 靜態定位精度測試結果Fig.7 Results of static positioning accuracy test

4.2.2 階躍響應性能測試

動態性能是系統一個十分重要的指標，通過階躍響應可以測定系統的動態性能。采用360″的階躍位置指令作為期望軌跡信號進行跟蹤實驗。實驗結果如圖8所示。

從實驗結果中可以看出，采用PID控制方法系統產生了52.8%的超調量，調節時間為14 ms；基于ZPETC方法的超調量為57.7%，調節時間為10 ms；而基于PTC控制方法的超調量為30.3%，調節時間為5.5 ms。采用PTC方法系統的階躍響應性能明顯好于PID和ZPETC方法。

圖8 階躍響應性能測試結果Fig.8 Results of step response performance test

4.2.3 正弦信號跟蹤性能測試

實驗過程中采用PTC控制方法對頻率分別為50，100，300 Hz，幅值為0.1°的正弦位置指令進行跟蹤，實驗結果如圖9～圖11所示。

圖9 50 Hz正弦信號的跟蹤性能測試結果Fig.9 Tracking performance test results for 50 Hz sine signal

圖10 100 Hz正弦信號的跟蹤性能測試結果Fig.10 Tracking performance test results for 100 Hz sine signal

圖11 300 Hz正弦信號的跟蹤性能測試結果Fig.11 Tracking performance test results for 300 Hz sine signal

從實驗結果中可以看出系統對指令的跟蹤精度較高。

4.2.4 系統帶寬測試

利用正弦指令輸入對不同控制方法的閉環控制帶寬進行測試，結果如圖12～圖14所示。

圖12 基于PID控制方法的系統閉環帶寬測試結果Fig.12 Closed-loop bandwidth test results for PID control

圖13 基于ZPETC控制方法的系統閉環帶寬測試結果Fig.13 Closed-loop bandwidth test results for ZPETC

圖14 基于PTC控制方法的系統閉環帶寬測試結果Fig.14 Closed-loop bandwidth test results for proposed PTC

由圖12可以看出，采用傳統PID控制方法，當輸入正弦波頻率為340 Hz時，幅值下降到-3 dB時，相位滯后25.704°，相位滯后嚴重。

由圖13可以看出，基于ZPETC控制方法，當輸入正弦波頻率為360 Hz時，幅值下降到-3 dB時，相位滯后14.256°，相位滯后明顯改善，但對300 Hz以上頻率信號的跟蹤仍然存在一定誤差。

由圖14可以看出，基于PTC控制方法，當輸入正弦波頻率為375 Hz時，幅值下降10%，相位滯后9.72°，動態特性得到了明顯改善。

從實驗結果可以看出，在相同的輸入條件下，采用PTC控制方法相對于PID和ZPETC控制方法，在帶寬拓展上有明顯的提升。

5 結 論

本文針對音圈FSM設計了一種基于PTC的控制方法，實現了高精度、寬頻帶的FSM閉環控制。以某型音圈FSM為實際被控對象進行了實驗驗證，并與傳統的控制方法進行了對比。實驗結果表明，本文設計的PTC控制方法能夠很好地保證反射鏡的跟蹤性能，相對于傳統的PID控制方法，系統階躍響應的調節時間縮短57%，系統的位置穩態誤差由0.3%減小到0.05%，系統靜態位置波動峰峰值減小50%；相比于ZPETC控制方法，系統階躍響應的調節時間縮短50%，位置穩態誤差由1.5%減小到0.05%；同時，采用PTC控制方法對幅值為360″的正弦指令進行跟蹤性能測試時，系統的雙十帶寬(幅值下降10%，相位滯后10°)可以達到375 Hz。由實驗數據可以看出，采用PTC控制方法，FSM的靜態定位精度以及動態響應性能相對于PID控制方法以及ZPETC控制方法有明顯的提高。本文設計的PTC控制方法可以有效抑制模型不確定性以及外部擾動的影響，提高系統的魯棒性，同時彌補了外部指令周期與快速反射鏡控制周期不同步的問題。