基于自適應窗口的線結構光條中心提取方法

萬卓仁，賴磊捷

(上海工程技術大學機械與汽車工程學院，上海 201620)

0 引言

近年來，基于線結構光的三維視覺檢測技術以高精度、非接觸性和快速等優點，被廣泛應用于缺陷檢測、非接觸檢測等領域[1]。在線結構光視覺測量系統中，快速、準確地提取光條中心，是得到目標物體三維信息的關鍵步驟[2]。有學者提出以光條的高斯分布中心為結構光中心的方法，來確定光條中心位置。基于這一思想，發展了極值法、閾值法[3]、灰度重心法[4]、曲線擬合法[5]和Steger法[6]等方法。

本文提出了一種基于自適應窗口的灰度重心法，用于提取結構光光條中心。該方法融合了其曲線擬合法和灰度重心法的各種特點。首先，對數字圖像進行預處理；其次，進行高斯曲線初步擬合，根據高斯曲線的特性自動選取閾值，能夠自適應地確定窗口范圍；最后，使用灰度重心法確定光條中心位置。

1 改進的灰度重心法

本文基于上述分析，提出了一種自適應選擇光條寬度的線結構光光條中心提取算法。算法的詳細步驟如下。

①利用八鄰域差值濾波法對數字圖像進行濾波。

②使用Otsu法進行圖像分割。

③取部分樣本數據進行高斯擬合，并記錄高斯曲線的均值和標準差。

④根據光條每行或每列的均值和標準差，使用高斯曲線能量分布的3σ準則自適應選取窗口大小，并計算窗口內數據灰度重心。

1.1 八鄰域差值濾波法

在實際工業環境下，高斯噪聲和椒鹽噪聲對數字圖像的影響是巨大的。因此，首先要對噪聲進行處理。由于光源的不穩定性和被測物自身的反光，導致各位置光條中心的灰度都不相同，所以通過中值濾波的方式無法把握統一尺度[7]。

本文提出了自適應八鄰域差值法，用于濾波處理。具體方法如下。

①運用3×3的八領域模板，如圖1所示。

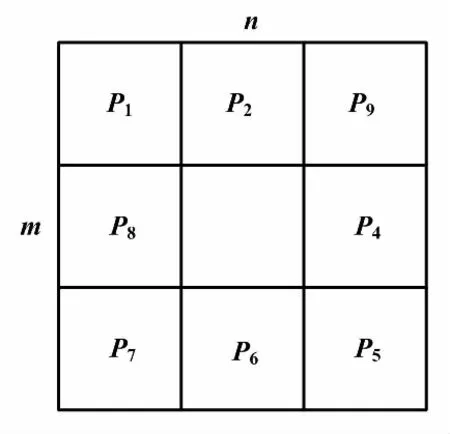
圖1 八鄰域模板Fig.1 Eight-neighborhood template

②在二維數字圖像中滑動，使模板中心與圖像中的像素點Pmn重合，模板中心外八鄰域像素值分別記為P1，P2，…，P8。

③計算各個像素點與中心像素灰度值的差值V1=|P1-Pmn|V2=|P2-Pmn|,…,V8=|P8-Pmn|，并設定閾值T。

(1)

將以上八個差值與T相比，如果大于T則認為該像素點是噪聲，應當剔除。通過該方法，可以有效剔除大部分噪聲，完全剔除遠離光條中心的噪聲，且不影響光條的邊緣，保留了圖像的細節。

1.2 Otsu法分割圖像

圖像分割就是將一副圖像分割成不同的部分(被測目標與背景)，舍去背景部分，保留目標信息。該方法大大減少了計算時的數據量，提高了檢測精度。在分割圖像中，閾值分割較為常用，特別適合目標灰度值和背景灰度值有較大差異的圖像。Otsu法[8]作為一種自適應的圖像分割方法，被認定是最合理的圖像閾值分割方法。因此，本文將Otsu法作為圖像分割方法，在MATLAB中能通過函數直接實現。

1.3 自適應窗口的灰度重心法

理想情況下，由激光器發射的激光在被測物體表面形成的光條，在其法向方向的截面上光條的能量強度呈高斯分布[9]，光條橫截面的像素值近似服從高斯分布，所以可以用高斯曲線擬合的方法進行初步擬合。設高斯曲線表達式為：

(2)

式中：f(x)為灰度值函數；A為幅值；μ為均值，即條紋中心；σ為標準差。

對式(2)的等式兩邊同時取對數，得到：

(3)

此時，就可以把高斯擬合看作二次多項式擬合。

逐行掃描分割后的圖像，在每一行中記錄光條寬度以及邊緣坐標。在光條總寬上等距取N個點進行初步擬合。這N個采樣點可以記為]xi,f(xi)]。其中，xi為該行的第i個像素點的列坐標。利用最小二乘法進行多項式的擬合，就可以確定[μ,σ,A]的值。

服從高斯分布的概率密度函數為：

(4)

根據概率密度的特性，68.27%的高斯能量聚集在[μ-σ，μ+σ]的范圍內，95.45%的高斯能量聚集在[μ-1.96σ，μ+1.96σ]的范圍內，99.74%的高斯能量聚集在[μ-3σ，μ+3σ]的范圍。只要將擬合得到的高斯曲線乘上系數A*，即可得到g(x)。

(5)

雖然每個點的灰度值大小發生變化，但是能量分布卻不會發生變化，條紋中心的位置也不會發生變化，同樣滿足概率密度的分布。

王順等根據各種情況下的高斯模型比較，提出以光條橫截面所具有的能量和為光條中心點信度的評價依據是符合實際情況的[10]。因此，可以以激光的能量分布情況來確定條紋中心的位置。在高斯模型中，條紋中心落在[μ-3σ，μ+3σ]以外的概率小于0.3%。在實際應用中，常認為該事件是不會發生的，基本可以將這個區間看作是條紋中心取值區間。這就是高斯分布的“3σ原則”。因此，可以根據被測對象的特性來選取合適倍數的σ，作為灰度度心法的計算區間。本文根據3σ原則，自適應地確定區間長度，采用高斯擬合的方法求出每行3σ和μ的值，并使用[μ-3σ，]μ+3σ]作為該行灰度重心法的計算窗口，在此范圍內使用灰度重心法。

(6)

當所有行全部執行結束后，即可得到提取出的光條中心。

2 試驗與分析

為驗證光條提取算法有效性，本文搭建了基于單線結構光的視覺測量系統。系統使用大恒圖像的MER-130-30UM型數字相機，其分辨率為1 280×1 024；鏡頭使用大恒新紀元科技股份有限公司的GCO-260611物方遠心測微鏡頭。試驗中，利用線型激光器向被測對象發射激光，攝像機拍攝被測對象，并用本文提出的算法對光條圖像進行處理。其中，攝像機、激光器以及被測工件這三者之間的位置滿足三角法測量系統的位置分布要求[11]。

圖2是攝像機采集到的原始激光圖像，即線結構光照射到一個圓臺表面形成的曲線圖像。

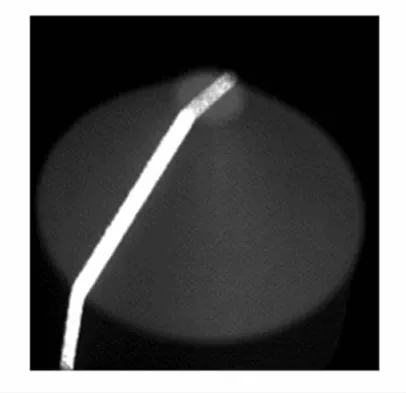
圖2 原始激光圖像Fig.2 Original laser image

對圖2進行自適應八鄰域差值濾波，并采用Otsu法分割后，得到預處理后圖像，如圖3所示。

圖3 預處理后圖像Fig.3 Pre-processed image

光條中心圖像如圖4所示。圖4(a)為通過自適應窗口的灰度重心法求出的光條中心，圖4(b)為圖4(a)的局部放大。

圖4 光條中心圖像Fig.4 Image of light stripes center

以上提取出的光條中心曲線是在噪聲很小、光照理想的情況下得到的。實際工業環境卻較為惡劣，所以需要通過加噪聲，改變外部光照條件來模擬實際的環境。圖5是攝像機在同一個位置、不同光照強度和噪聲下采集的激光條紋圖像。圖5(a)～圖5(c)分別是在不同光照下得到的圖像，圖5(d)是在圖5(b)的基礎上人為加入了椒鹽噪聲以及高斯噪聲后，得到的中等光照圖像。

圖5 不同外部條件下的線結構光條紋圖像Fig.5 Images of line structured light stripes under different external conditions

分別采用傳統的灰度重心法、梅俊華等人提出的融合極值法的灰度重心法、基于自適應窗口的灰度重心法提取激光條紋中心。對比每種方法的第400、450行提取結果,如表1所示。

由于在實際測量中，光條真實中心無法測量，因此常用殘差v代替真差，然后按照Bessel公式計算標準誤差的值：

(7)

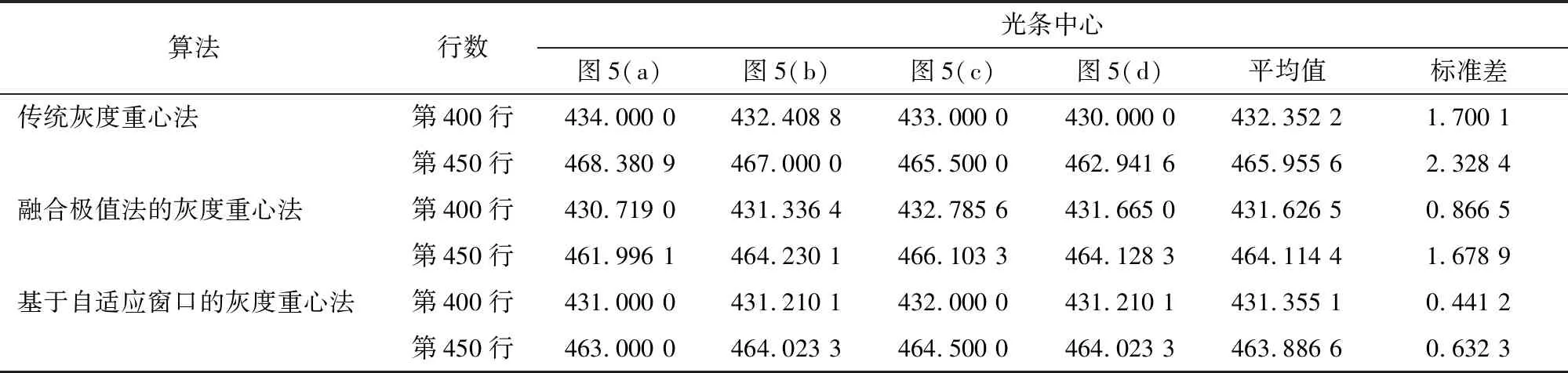
表1 不同條件下提取光條中心的對比Tab.1 Comparison of strip centers extgracted by different methods

由表1可知，對比圖序號圖5(b)和圖5(d)，可驗證噪聲對光條中心提取的影響：人為加入噪聲后對于傳統的灰度重心法平均殘差為1.96 pixels，對于融合極值法的灰度重心法平均殘差為0.33 pixels，對于自適應窗口的灰度重心法平均殘差幾乎為0。由此可以說明工業噪聲對于傳統方法的影響較大，不能滿足實際工業需求。而融合極值法的灰度重心法和基于自適應窗口的灰度重心法的抗噪聲能力高于傳統的灰度重心法。

對比圖5(a)～圖5(c)，可驗證光照強度對光條中心提取的影響。圖5光照強度由強變弱：傳統灰度重心法在較強光、中等光、弱光下的平均殘差分別為2.36 pixels、0.55 pixels、0.10 pixels；融合極值法的灰度重心法在3種光強下的平均殘差分別為1.51 pixels、0.09 pixels、1.57 pixels；本文算法在3種光強下的平均殘差分別為0.62 pixels、0.64 pixels、0.14 pixels。在實際應用中多采用弱光條件。 因此，基于自適應窗口的灰度重心法魯棒性和精確度優于其他兩種算法。

對比以上四種條件下的標準誤差，基于自適應窗口的灰度重心法(0.54)比傳統的灰度重心法(2.01)和融合極值法的灰度重心法(1.27)效果更好。綜上所述，基于自適應窗口的灰度重心法具有很好的魯棒性和精確度。

同時，在光照和噪聲一致的環境下，對比近些年來最新提出的光條中心提取算法(融合極值法的灰度重心法、劉劍等提出的基于海森矩陣和區域增長的提取方法[12]、甘宏等提出的雙閾值自適應分割方法和本文提取方法)的標準誤差和運行時間。同一條件下，不同方法標準方差和運行時間的對比如表2所示。

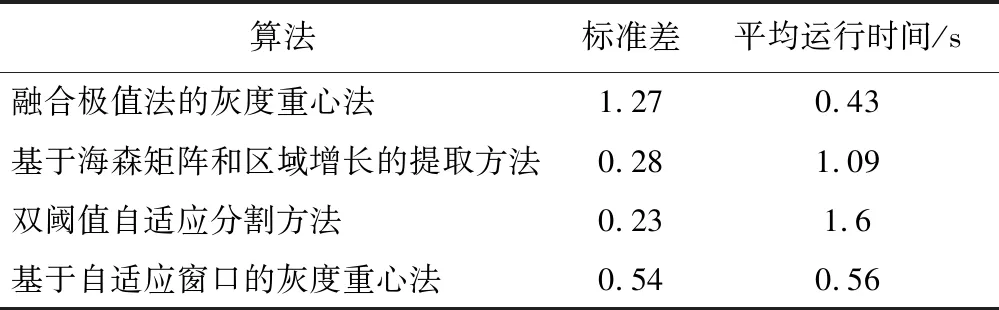
表2 同一條件下不同方法標準方差和運行時間的對比Tab.2 Comparison of standard variance and running time of different methods under the same condition

由表2可知，隨著標準誤差的減小，運行時間不斷增大。融合極值法的灰度重心法運行時間最快(0.43 s)，但是標準誤差(1.27)較大，精度不能滿足檢測需求。基于海森矩陣和區域增長的提取方法和雙閾值自適應分割方法精度比較高。但這兩種方法運行時間已經不能滿足實時性的要求。本文所提出改進的算法在計算速度和預測精度之間達到了平衡，比較適合實際的工業環境。

3 結論

線結構光光條中心提取是視覺測量的主要步驟，直接決定了整個視覺測量系統的優劣。本文提出一種自適應窗口線結構光光條中心高精度算法。該方法將高斯曲線特性和傳統的灰度重心法相結合，通過自適應窗口灰度重心法提取得到的光條中心位置的最大殘差、標準誤差和運行時間均優于傳統方法下得到的光條中心的最大殘差、標準誤差和運行時間。試驗結果表明，通過分析高斯曲線能量分布自適應地調整窗口大小，再進行灰度重心的計算，能很好地消除實際工業環境中噪聲和外部光照強度改變帶來的影響，使精度與運行時間達到一定的平衡。這對于線結構光在工業領域應用意義更加突出。