樹形圖及其拓展在多元抽象復合函數求導中的應用

張 偉

(江蘇海事職業技術學院，南京 211170)

一元復合函數求導法則又稱鏈式法則，不僅是因為其關系圖y-u-x像一條鏈子，也不僅是因為求導法則很困難，更重要的是因為想到鏈式法則就想到了繃斷的鎖鏈。通過該法則，可以掙脫求導問題的束縛，對很多類型的函數進行求導。將鏈式關系圖推廣到樹形圖，在理解多元復合函數求導法則的基礎上找到計算其二階偏導數的簡便方法。

1 普通樹形圖的使用方法及實例分析

1.1 多元函數與多元函數復合的情形

定理1：若函數u=φ(x,y),v=ψ(x,y)在點(x,y)處具有對x及y的偏導數，函數z=f(u,v)在對應點(u,v)處具有連續偏導數，則復合函數z=f[φ(x,y),ψ(x,y)]在點(x,y)處的兩個偏導數都存在，且有：

(1)

借助于復合函數的函數結構圖——樹形圖對復合函數求偏導數的過程進行分析。

因變量z是中間變量u,v的二元函數從z出發分出兩條線，u,v都是自變量x,y的二元函數，所以再各自分出兩條線，畫樹形圖，如圖1所示。

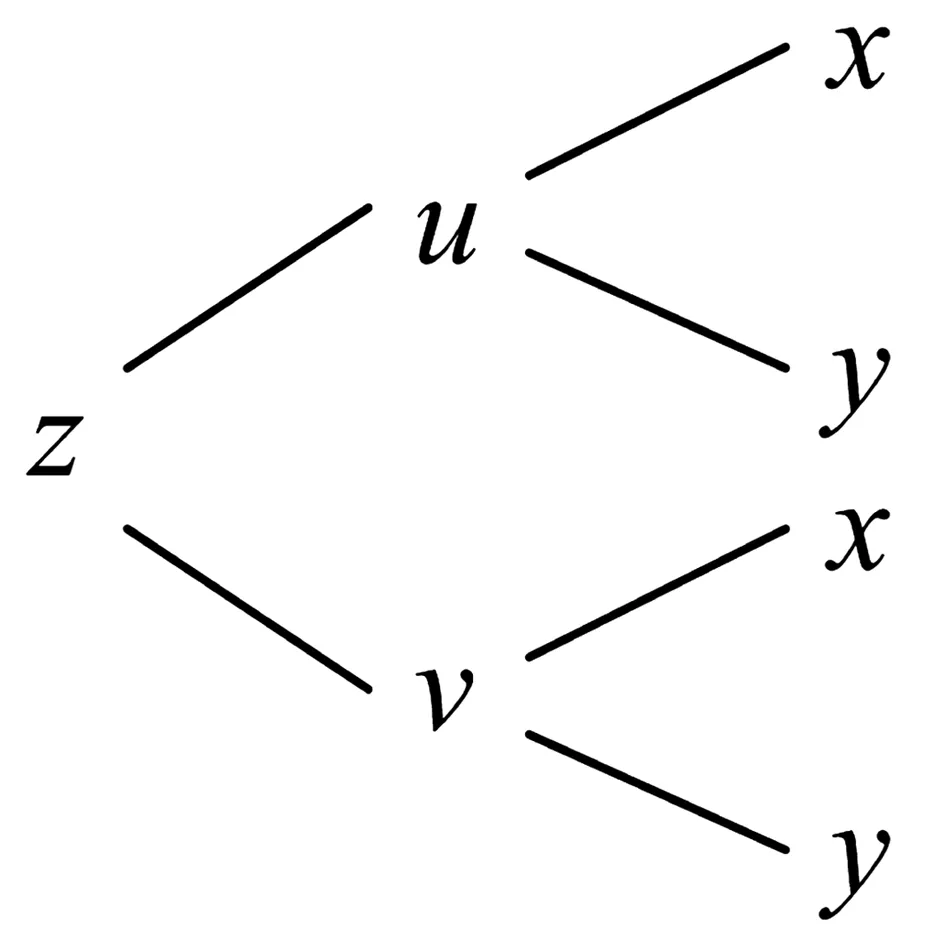
(圖1)

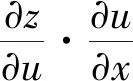
引入中間變量：u=x2y，v=x-y，則z=f(u,v)，樹形圖如圖1所示，從z到x有兩條路徑：z-u-x和z-v-x，根據定理1，有：

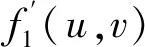
(圖2)

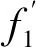
于是：

1.2 其他情形

復合函數的類型很多，不再一一列舉，選擇一種自變量本身又是中間變量的情況作為代表。

例如u=φ(x,y)在點(x,y)處具有對x及y的偏導數，z=f(u,x,y)具有連續偏導數，則復合函數z=f[φ(x,y),x,y]在點(x,y)處的兩個偏導數都存在。此時因變量z是中間變量u,x,y的二元函數，從z出發分出三條線，u是自變量x,y的二元函數，所以再分出兩條線，畫樹形圖如圖3所示。

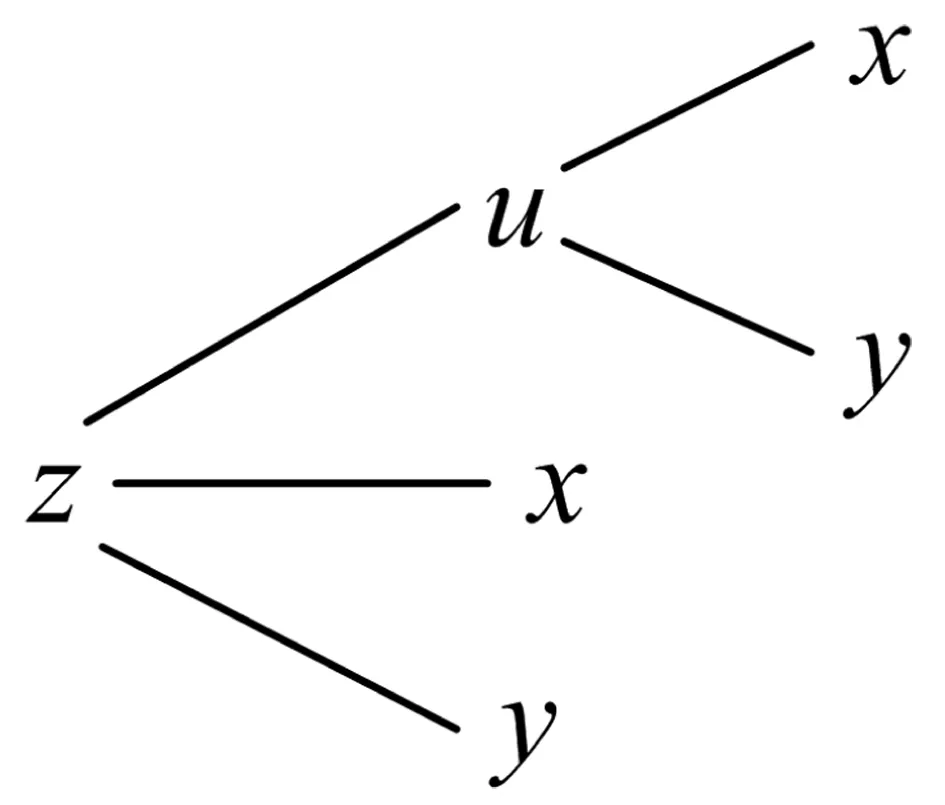
(圖3)

從圖3可以看出，從z到x有兩條路徑：z-u-x和z-x，根據“鏈乘相加”，可得復合函數z=f[φ(x,y),x,y]對x的偏導數：

類似可得對y的偏導數：

2 樹形圖拓展及實例分析

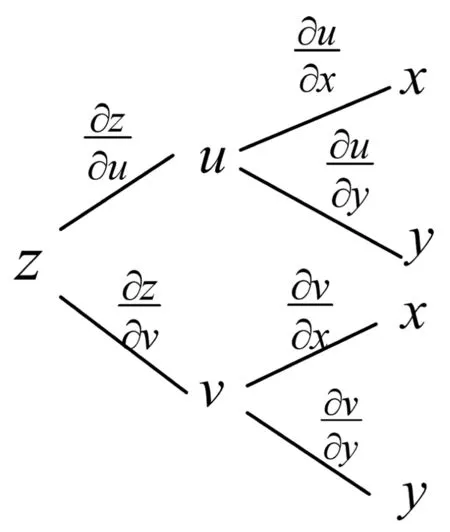
(圖4)

根據拓展的樹形圖對例1進行分析。

解：引入中間變量：

u=x2y，v=x-y,則z=f(u,v)，

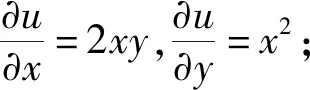
將上述偏導數寫在樹形圖上，如圖5所示。

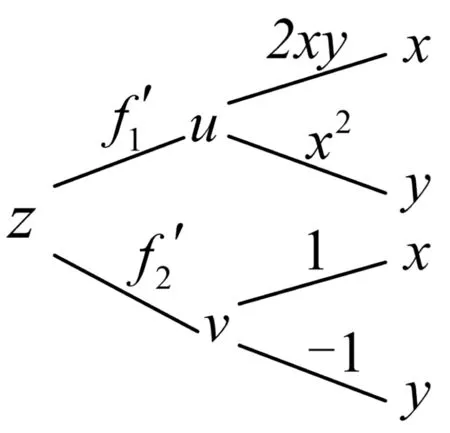
(圖5)

(圖6)

根據拓展的樹形圖還可很容易處理自變量本身又是中間變量，甚至更復雜的情況。

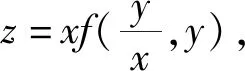
(圖7)

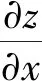
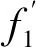
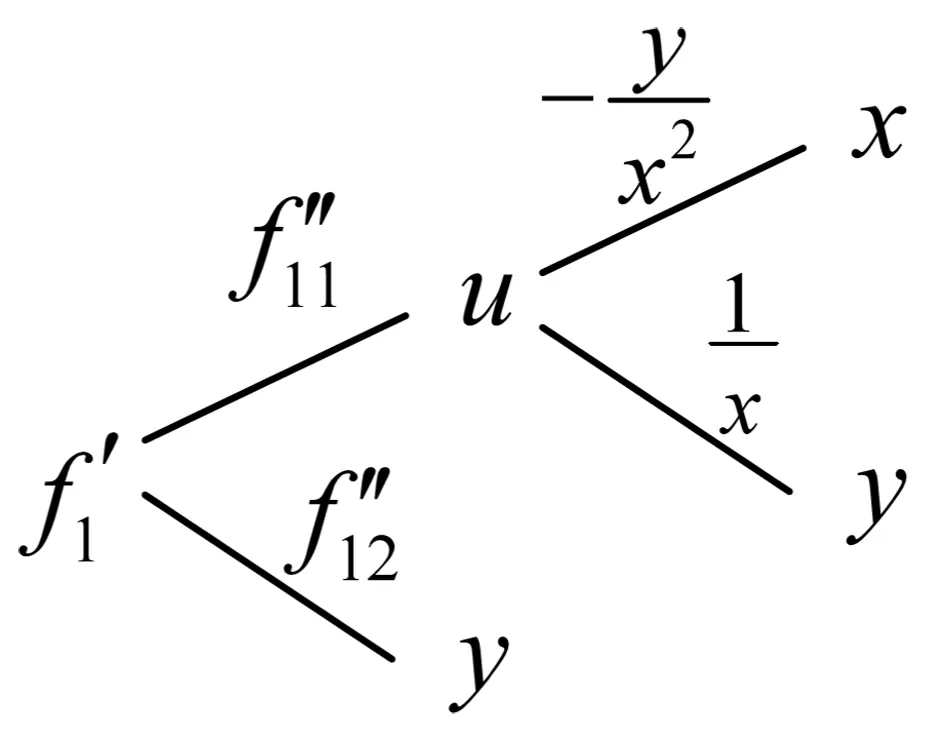
(圖8)

引入拓展樹形圖，使求多元抽象復合函數導數變得容易理解和計算，極大地提高了學生的學習效率。