異構分布式環境中的并行離群點檢測算法

王習特 朱宗梅 于雪蘋 白梅

摘? ?要：離群點檢測是數據挖掘領域研究的熱點之一，主要目的是識別出數據集中異常但有價值的數據點. 隨著數據規模不斷擴大，使得處理海量數據的效率降低，隨即引入分布式算法. 目前現有的分布式算法大都用于解決同構分布式的處理環境，但在實際應用中，由于參與分布式計算的處理機配置的差異，現有的分布式離群點檢測算法不能很好地適用于異構分布式環境. 針對上述問題，本文提出一種面向異構分布式環境的離群點檢測算法. 首先提出基于網格的動態數據劃分方法（Gird-based Dynamic Data Partitioning，GDDP），充分利用各處理機的計算資源，同時根據數據點的空間位置信息進行數據劃分，可有效減少網絡通信. 其次基于GDDP算法，提出了異構分布式環境中并行的離群點檢測算法（GDDP-based Outlier Detection Algorithm，GODA）. 該算法包括2個階段：在每個處理機本地，按照索引中數據點的順序進行過濾，通過2次掃描得到離群點候選集;判斷候選離群點需要進行網絡通信的處理機，使用較低網絡開銷得出全局離群點. 最后，通過大量實驗驗證了本文提出的GDDP和GODA算法的有效性.

關鍵詞：離群點檢測;異構分布式;網格;數據劃分

中圖分類號：TP391 ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標志碼：A

Parallel Outlier Detection Algorithm

in Heterogeneous Distributed Environment

WANG Xite?，ZHU Zongmei，YU Xueping，BAI Mei

（College of Information Science and Technology，Dalian Maritime University，Dalian 116000，China）

Abstract：Outlier detection is one of the hotspots in the field of data mining. The main purpose is to identify the abnormal but valuable data points in the data set. With the expansion of data scale，the efficiency of processing massive data is reduced，and then a distributed algorithm is introduced. At present，most of the existing distributed algorithms are used to solve the homogeneous distributed processing environment. However，in practical applications，due to the differences in processor configuration involved in distributed computing，the existing distributed outlier detection algorithms cannot be well applied to heterogeneous distributed environments. In view of the above problems，this paper proposes an outlier detection algorithm for heterogeneous distributed environments. Firstly，a grid-based dynamic data partitioning （GDDP） method is proposed，which makes full use of the computing resources of each processor and divides the data according to the spatial location information of the data points，which can effectively reduce the network communication. Secondly，based on the GDDP algorithm，a parallel GDDP-based Outlier Detection Algorithm （GODA） is proposed. The algorithm consists of two stages：in each processor，filtering according to the order of the data points in the index and obtaining the outlier candidate set by two scans;determining the candidate outliers requiring network communication and using low network overhead leads to global outliers. Finally，the effectiveness of the proposed GDDP and GODA algorithms is verified by a large number of experiments.

Key words：outlier detection;heterogeneous distribution;grid;data partition

離群點檢測是數據管理領域的重要研究內容之一，其主要目的是識別出數據集中與其他數據存在顯著差異的數據對象. 隨著對離群點的不斷研究，出現了多種離群點描述方式. 其中，最直觀的方式是通過度量數據空間中數據點間的距離來量化數據的離群程度. 具體地，基于距離的離群點可定義為：給定參數k和r，對于數據集P中任意數據點p，若與點p的距離小于等于r的數據點個數少于k，則p為離群點[1].

隨著數據庫中數據量的不斷增加，有關離群點的研究已從集中式處理環境轉向分布式處理環境，以提高海量數據的離群點檢測效率[2]. 但是，現有的分布式算法大都用來解決同構分布式環境中的離群點檢測問題. 在實際應用中，參與分布式計算的處理機大都存在配置上的差異，各處理機的性能可能存在較大差異. 這也就使得現有的針對同構分布式環境設計的離群點檢測算法不能很好地適用于異構分布式環境. 因此，迫切需要設計一種高效的異構分布式環境中的并行離群點檢測算法.

本文主要針對異構分布式環境下的離群點檢測問題，提出一種動態數據劃分方法和相應計算方法，旨在提高算法的執行效率. 具體地，本文的主要貢獻包括以下幾個部分：

1）提出一種基于網格的動態數據劃分方法GDDP（Gird-based Dynamic Data Partitioning）. 該方法依據異構分布式環境中各處理機計算能力的差異動態分配計算任務，實現了各處理機計算任務的負載均衡，加快了計算效率. 同時，考慮了數據集中數據點所處的空間位置信息，盡可能將空間上相鄰的數據點劃分至同一處理機，降低網絡開銷.

2）基于GDDP劃分方法，提出了異構分布式環境中并行的離群點檢測算法GODA（GDDP-based Outlier Detection Algorithm）. 該算法主要包括兩個過程：①本地離群點計算.首先通過索引對每個處理機本地的數據集進行管理，然后根據過濾規則實現數據集中非離群點的過濾，從而快速計算出本地離群點;②全局離群點計算.利用每個候選離群點和其所在數據塊與相鄰數據塊的距離關系，判斷需要進行網絡通信的處理機，然后統一將候選點發送到相應的處理機上，從而得到全局離群點.

3）分別利用真實數據集和人工合成數據集進行實驗，驗證了本文提出的GDDP和GODA算法的有效性.

1? ?相關工作

本節主要從集中式和分布式兩方面對離群點檢測的相關研究進行概述.

1.1? ?集中式離群點檢測

目前，大多數離群點研究都是面向集中式環境的. 研究內容主要包括兩個方面：離群點定義和離群點檢測方法. 首先，離群點定義方面的研究致力于給出一種描述或者形式化定義離群點的方法. Hawkins等[3]最早給出離群點的形象化描述，認為離群點是數據集中與其他點差距很大、且懷疑與其他數據點并非由同一機制生成的點. 為了更明確數據點是否為離群點，提出基于模型的離群點定義，以數據的分布模型為參考，將數據集中不符合分布模型的數據點定義為離群點[4]. 至今，研究人員給出了多種不同的離群點定義標準，如：基于距離的離群點、基于聚類的離群點[5]、基于密度的離群點[6]. 其中，基于距離的離群點定義能直觀地反應離群點本質進而得到廣泛應用.

其次，離群點檢測是指根據某種離群點判定方式，從數據集中快速找到符合該判定方式的數據點的過程，判定方式不同，相應的離群點計算方法也不同. 具體地，文獻[1]基于距離的離群點定義，提出一種嵌套循環方式，對數據集中每個數據點進行距離計算，以找出最終的離群點. 這種方法可以應對多維數據集，但實際的計算效率有待優化. 之后，Bay等[7]提出ORCA算法，利用緩沖區給出一種修剪規則，實現對非離群點的過濾，加快檢測效率. 此外，有些學者利用空間索引加速離群點的計算過程. 文獻[8] 提出了基于R樹的離群點檢測算法，文獻[9]給出了基于k-d樹的離群點檢測算法.

1.2? ?分布式離群點檢測

為了解決傳統集中式離群點檢測算法在大規模數據中檢測效率低的問題，許多研究人員提出了有效的分布式算法，而現有的分布式離群點檢測算法都是面向同構分布式環境的. Hung等[10]首先給出分布式環境中基于距離的離群點檢測算法，將數據均勻劃分至各處理機，然后對傳統嵌套循環算法進行優化，實現分布式的離群點計算過程. 文獻[11]首先提出了GBP數據劃分方法，利用網格空間索引結構對數據進行管理和劃分，然后基于GBP劃分方法給出分布式離群點檢測算法DLC. 同樣地，針對同一離群點定義，文獻[12]也提出了相應的分布式離群點計算方法，在處理具有偏態分布的數據集時非常有效. 文獻[13]首先提出了BDSP數據劃分算法，可以有效均衡各計算節點的工作負載，同時實現良好的過濾效果，然后利用BDSP方法提出基于距離的分布式離群點檢測算法BOD，有效減少網絡開銷，縮短了離群點的計算時間. 此外，文獻[14]還給出了利用GPU并行地計算離群點的策略.

雖然已有一些優秀的分布式離群點檢測方法，但這些方法都是針對同構分布式環境設計的，在異構分布式環境中無法保證高效的離群點檢測效率.

2? ?問題描述

本文主要研究在異構分布式環境中，如何并行地計算出數據集內所有基于距離的離群點. 下面，具體地給出基于距離的離群點的形式化定義，其中，表1列出了本文使用的符號及其含義.

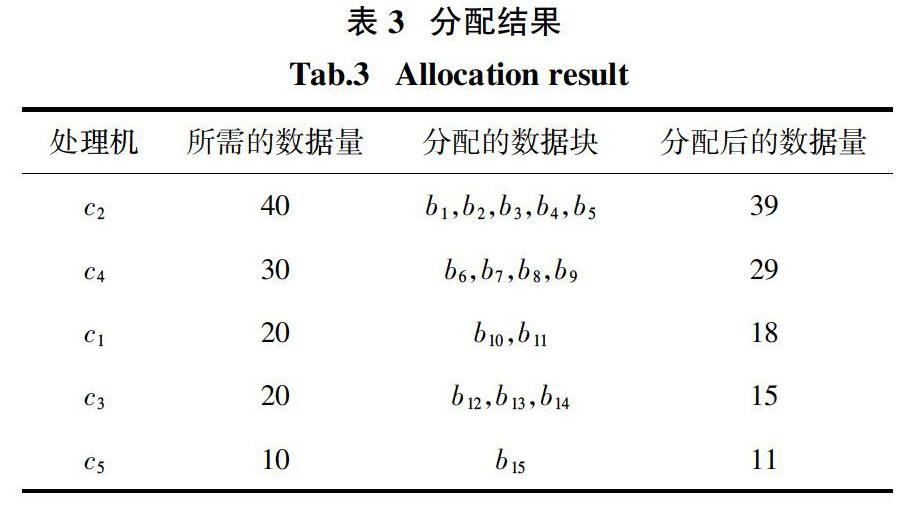
一般地，給定一個具有d維屬性值的數據集合P. 對于P中任一數據點p可表示為： p

p[3]，…，p[d]>，那么對于數據集P中任意兩個數據點p1和p2之間的歐式距離的計算公式為：

3? ?異構分布式中的離群點查詢處理框架

本文主要針對異構分布式環境，其整體上包含一臺主控制節點和數目固定的多個從節點C = {c1，c2，…，cn }. 由于各節點間數據遷移量較小，本文不考慮網絡異構，其異構環境特指每個參與計算的從節點的配置各不相同，使得它們在計算能力上存在差異. 另外，主控節點和每一個從節點都通過網絡互連，可以進行網絡通信. 每兩個相鄰的從節點之間也可相互通信. 為了防止主控節點在計算過程中發生擁塞，在數據劃分時將不給主控節點分配計算任務，即在整個基于距離的離群點計算過程中，主控節點主要負責計算任務的調度，大部分的離群點計算任務都將由從節點完成.

根據圖1中的查詢處理框架，異構分布式環境中的基于距離的離群點檢測任務可以被描述為：對于給定的數據集合P、查詢距離閾值r和查詢數量閾值k，通過充分利用異構分布式計算框架中各異構處理機的計算能力，快速地計算出給定數據集合P中的所有基于距離的離群點.

具體地，整個過程大致可分為3個階段：

1）數據劃分階段. 對于給定數據集P，主控制節點首先依據各異構處理機的計算能力的不同對數據集進行劃分，然后將劃分后的子數據集發送至相應的處理機.

2）局部離群點計算階段. 各個參與計算的處理

機在接收到對應的數據子集合后，在本地進行局部計算，得到局部離群點，最后將它們發送到主控制節點.

3）全局離群點計算階段. 主控制節點根據接收

到的局部離群點的位置信息判斷其需要通信的從節點，然后將它們發送到相應處理機再次進行距離計算，得出最終的全局離群點.

4? ?基于網格的動態數據劃分方法

在離群點檢測之前，對數據集進行有效的劃分，可以顯著提高離群點檢測效率. 本文提出的基于網格的動態數據劃分方法GDDP保證了計算資源的充分利用，具有較高的負載均衡性.

4.1? ?計算能力評估

在分布式計算系統中為了能夠實現整個系統的高可用性，一般需要實現各個參與計算的處理機之間負載均衡. 在異構分布式環境中，各處理機間的計算能力不同，為了能對計算任務進行合理的分配，需要對每個處理機的計算能力進行評估.

首先，查詢處理框架中的主控制節點會將相同的一份測試數據集發送給每個參與計算的從節點，進行相同的任務計算，然后記錄每個處理機完成任務的時間. 其中，處理機完成任務的時間越短，說明其計算能力越強;反之，其計算能力越弱.

為了便于后續基于網格的數據集的劃分，本文給出一種有效的評分機制. 首先，將工作節點的計算能力劃分為m個等級，即β1，β2，…，βm，對應得分分別為1，2，3，…，m，相應的工作節點的計算能力依次增強;其次，求出每個從節點的計算能力與當前最大計算能力的比值，所得結果在（0，1]內，其中，將（0，1]劃分為m等份，表示（0，1/m]，（1/m，2/m]，…，（m-1/m，1]，所得比值在各區間內的處理機的等級分別為β1，β2，…，βm;最后，根據每臺處理機的計算能力等級得出相應的評分. 例如，在一個異構分布式系統中有c1～c5 5臺從節點，為簡化示例，此處等級數m=4，由以上方法得出各處理機的計算能力評估表如表2所示.

4.2? ?數據集劃分

傳統的數據劃分方法對維度過高的數據集進行處理時，會產生巨量的劃分子塊，致使檢測效率低下，由此本文決定對給定的多維數據集中數據分布最均勻的二維空間利用網格進行數據劃分，經數據劃分后會形成多個二維的數據子塊.

首先確定數據集中每一維數據需劃分為幾段. 考慮在異構分布式環境中，各從節點的計算能力不同，由此具體的劃分段數為：

其中，comp_Grade（ci）表示處理機ci的計算能力得分，n表示處理機的數目. 例如，根據表2中對5臺異構處理機c1 ～ c5計算能力的評估結果，結合公式（2）可得劃分段數Segment值為4，因此，數據集將被映射到一個4×4規模的網格結構內.

其次，為了判斷數據在哪個維度上分布最均勻，本文給出一種衡量標準. 具體地，數據在第d維上分布的均勻程度為：

single_U（d）的值越小，說明數據在第d維上分布越均勻. 其中，num（segment（i））表示數據在第d維上的第i個劃分段內的實際分布數量;μ表示數據在第d維上每個劃分段數內的平均分布數量，它等于數據集的大小與劃分段數Segment的比值;n取值為劃分段數Segment的值.

接下來，數據在由d1和d2維所組成的二維空間內的分布均勻程度用multi_U（d1，d2）來描述. 同樣地，multi_U（d1，d2）的值越小，表明數據在該二維空間內分布越均勻. 具體地，multi_U（d1，d2）的計算公式表示為：

式中：num（gi）表示數據在當前d1和d2維空間內所建立的網格索引中第i個網格內的實際分布數量;n表示二維網格中網格的數目，其值等于劃分段數Segment的平方;μ表示數據在每個網格內的平均分布數據，其值等于數據集的總量與網格數目的比值.

由以上數據分布均勻程度的兩個衡量過程，可確定給定數據集中數據分布最均勻的二維空間，從而完成數據集的劃分. 具體地，對于給定的具有d個維度的數據集的劃分過程大致為：首先，根據劃分段數Segment將數據集的每一維度劃分成s個區間，然后統計數據在每個區間內的分布情況，并根據計算得出數據在每一維上的single_U（d）值，選擇single_U（d）值最小的 [] 個數據維度作為候選目標;其次，在候選維度里面，根據劃分段數Segment，依次選取兩個維度建立二維網格，并評估數據在二維網格內的分布情況;最終，根據multi_U（d1，d2）值最小的二個維度上對應的網格對數據集進行劃分，可以得到多個不相交的劃分數據子塊.

4.3? ?數據塊的分配

當數據集被分成多個不相交的數據子塊后，緊接著需將其合理地分配到各異構的從節點上.

4.3.1? ?分配順序

根據基于距離的離群點定義，為了減少分布式計算過程中各處理機之間的通信代價，需要將空間中鄰近的數據點盡量分配到同一臺工作節點上. 因此，在數據塊的分配過程中首先需要考慮數據集劃分后各數據塊之間的相鄰關系，這樣才能盡可能將空間中相鄰的數據對象分配到同一臺工作節點上. 由于劃分時用到的是二維網格，本文則按照網格的行序將相鄰的數據塊依次進行分配即可保證數據塊之間是相鄰的，如圖2中箭頭所指方向即為數據塊的分配順序.

4.3.2? ?分配規則

在本文所指的異構分布式環境中，對于參與計算的異構處理機，按照其計算能力由大到小順序排列，之后優先選擇計算能力強的處理機進行數據塊的分配. 如下算法1給出了具體的數據塊分配過程.

經過上述分配過程，可以完成數據集中大多數數據的初分配，并且分配后大多數處理機都能獲得小于等于其實際所需的數據量.

例如，給定多維數據集P，且|P|=120. 如表2所示，有5臺異構的從節點參與離群點的計算，對應的c1～c5處理機順序為：c2、c4、c1、c3、c5. 圖3所示為數據集劃分的結果，則數據塊的分配順序為b1～b16 . 首先對處理機c2進行數據塊分配，計算可得其所需數據量為×120 = 40. 優先處理數據塊b1，由于塊內數據量5小于c2當前所需數據量40，則將b2分配給處理機c2，同時更新c2當前所需數據量為35，最終，數據塊b1、b2、b3、b4、b5都可被分配給c2，當對數據塊b6進行分配時，由于處理機c2目前所需要的數據量為1，小于數據塊b6的數據量，所以停止對處理機c2的數據塊分配. 同理，可依次完成處理機c4、c1、c3、c5的數據塊分配任務.

具體的分配結果如表3所示. 這樣經過數據塊的分配后，只有處理機c5所分配的數據量略大于它實際所需要的數據量. 同時，只有數據塊b16未被分配，把它暫時留在主控制處理機上.

4.4? ?動態數據分配

動態分配旨在對存儲于主控制節點上的剩余的未被分配的數據塊進行數據分配. 為了對空閑處理機進行準確的任務分配，主控制節點需記錄從開始執行計算任務到有空閑節點出現所經過的時間，即當前空閑的處理機ci完成初始的分配任務的時間t，以及在處理時間t內每個處理機已經處理的數據量complete_num（ci），由此可計算出各處理機在當前所劃分的數據集中進行離群點檢測任務時的實時處理速度vi（其中，vi = ）;同時，用當前未被處理的數據總量除以各處理機處理速度之和還可預估出剩余的所有計算任務完成的時間T;最后，將時間T和空閑處理機的實時處理速度vi相乘，即可得出當前空閑工作節點所應分配的數據量. 當存儲在主控制節點上的數據都被分配后，動態分配過程結束.

這種動態數據分配方法依據各處理機的實際處理速度進行計算任務的分配，盡可能地避免了空閑處理機的等待，并充分利用了整個異構分布式環境中各處理機的計算資源，加快了離群點的檢測速度.

5? ?GODA算法描述

本節主要描述了GODA算法的具體細節. 整個過程分為2個階段：1）本地離群點計算，即利用每個處理機的計算能力計算出本地離群點;2）全局離群點計算，即通過全局通信確定最終離群點結果集.

5.1? ?本地離群點計算

本小節主要闡述GODA算法中一種有效的面向多維大規模數據集的本地離群點計算方法.

5.1.1? ?索引構建

由于網格索引、R樹索引等一般的空間索引無法應對數據集維度的增長，并且根據離群點的形象化描述，在給定的數據集中，大部分數據點都是非離群點，而離群點只占據數據集的很少一部分，因此，本文索引構建采用如下方法.

在給定數據集中隨機選取一個數據點p，其中，點p在很大程度上為非離群點，以點p為中心，計算數據集中其他數據點到點p的距離，依據距點p由近及遠的順序對數據進行管理，如果數據點q距離中心點p很遠，則說明點q很可能是離群點.

5.1.2? ?本地離群點計算方法描述

首先，對于給定數據集P中的數據點p，自定義數據結構node如下：

1）給定數據集P中的一個數據點p;

2）數據點p在給定數據集P中的唯一標識，用

p.id表示;

3）數據點p在給定數據集P中的鄰居情況，用

p.nn表示;

4）數據點p與其第k個近鄰點的距離，用p.r表示.

其中，p.nn是一個大小為k（用戶給定的查詢數量閾值）的列表，用于存儲數據集P中與數據點p的距離不大于用戶給定的查詢距離閾值r的數據點q的標識以及點q與點p間的距離dist（p，q）;對于p.r，當p.nn的大小為k時，p.r等于存儲在p.nn中最大的距離值;當p.nn的大小小于k時，p.r的值被設為+∞.

在離群點計算過程中，根據點p的node結構中p.r的值與查詢距離閾值r的大小關系即可判斷當前數據點p是否為離群點. 例如，若p.r的值小于等于查詢距離閾值r，那么數據點p是非離群點;若p.nn列表未存滿，且p.r取值為+∞，則點p是離群點.

根據上述自定義的node結構，給出非離群點過濾定理.

定理1? ?對于當前掃描到的數據集P中的數據點q，如果它和內存中存儲的數據點p之間的距離滿足dist（p，q）≤r-p.r，則數據點q為非離群點.

證? ?根據dist（p，q）≤r-p.r可得p.r≤r，則說明內存中的數據點p為非離群點，且在p.r范圍內數據點p的鄰居個數至少為k個. 又因為數據點p和數據點q之間的距離滿足dist（p，q）+ p.r≤ r，則說明數據點p及其鄰居都是數據點q的鄰居，也即數據點q的鄰居個數大于給定的數量閾值k，因此根據基于距離的離群點定義可得數據點q為非離群點.?? ? ? ? 證畢.

根據索引中數據點的順序及定理1中的過濾規則，每個處理機通過掃描兩次數據集可實現本地離群點的計算過程. 算法2給出了本地離群點檢測的具體過程.

算法2? ?本地離群點檢測算法.

輸入：查詢距離閾值r，查詢數量閾值k，本地存儲的數據集P;

輸出：本地離群點集合

1. 初始化隊列H為空;

2. FOR 數據集P中的每個數據點p? DO

3.? ? 初始化p的信息，p.nn為空，p.r為+∞;

4.? ? IF H為空 或者 IsNoInlier（p）? THEN

5.? ? ? ?將數據點p加入到隊列H中;

6.? ? ENDIF

7. ENDFOR

8. FOR H中的每一個數據點q DO

9.? ? 將滿足q.r不大于查詢半徑r的數據點從H中刪除;

10. ENDFOR

11. FOR 數據集P中的每個數據點p? DO

12.? ? DeleteInlier（p）;

13. ENDFOR

14. 隊列H中的數據點全部都是離群點，輸出;

第一次掃描數據集時，需要將當前掃描到的不能確定是非離群點的數據點的node結構存儲到內存中，以致于第一次掃描結束后，內存中至少存儲著所有的本地離群點的信息. 由此，判定數據點p不是非離群點的IsNoInlier（p）函數的算法如下：

IsNoInlier（）

輸入：查詢距離閾值r，查詢數量閾值k，查詢數據點p，隊列H;

輸出：數據點p的查詢結果

1. FOR H中的每一個數據點q? DO

2.? ? IF dist（p，q）≤r-p.r? THEN

3.? ? ? 數據點p為非離群點，返回FALSE;

4.? ? ? BREAK;

5.? ? ENDIF

6.? ? IF dist（p，q）≤r THEN

7.? ? ? 利用臨時變量oldr記錄數據點q的q.r值，并將p更新到q的

q.nn列表中;

8.? ? ? IF oldr>r 并且 q.r≤r THEN

9.? ? ? ? 以0.5的概率將數據點q從H中刪除;

10.? ? ? ENDIF

11.? ? ? 將q更新到p的p.nn列表中;

12.? ? ? IF p.r≤r? THEN

13.? ? ? ? 數據點p為非離群點，返回FALSE;

14.? ? ? ENDIF

15.? ? ENDIF

16. ENDFOR

17. IF p.r>r THEN

18.? ? 返回TRUE;

19. ENDIF

第二次掃描數據集時，即從所有的候選本地離群點集合中找出真正的本地離群點，其中，刪除內存中非離群點的DeleteInlier（p）函數的算法如下：

DeleteInlier（）

輸入：查詢距離閾值r，查詢數量閾值k，數據點p，隊列H;

輸出：隊列H

1. FOR H中的每一個數據點q? DO

2.? ? IF dist（p，q）≤r THEN

3.? ? ? 將p更新到q的q.nn列表中;

4.? ? ? IF q.r≤r THEN

5.? ? ? ? 將數據點q從隊列H中刪除;

6.? ? ? ENDIF

7.? ? ENDIF

8. ENDFOR

總體上，本小節基于距離的本地離群點計算方法可以通過掃描較少次數的數據集完成離群點的檢測過程，在一定程度上減少了IO代價，同時，還可以很好地應對數據集中數據維數的增長.

復雜度分析：記本地數據集的大小為N. 對于本地離群點的計算，構建索引所需時間復雜度為O（N·lgN），兩次掃描數據集所需的時間復雜度為O（|H|·N）. 因此，算法2的時間復雜度為O（N·lgN+|H|·N）.

5.2? ?全局離群點計算

在完成5.1節的計算之后，本地離群點被發送到主控制節點形成離群點候選集，此后由主控制節點判斷其所需進行網絡通信的處理機，進而計算出真正的離群點.

對于給定的數據集P，利用GDDP劃分方法對數據分布最均勻的二維空間（假設是d1和d2維所

組成的空間）劃分后所得的數據塊b可表示為b =

[b.min，b.max]. 其中，b.min、b.max分別表示數據塊b的下界和上界，則對于數據塊b中的任意數據p，

都有b.min[d1]≤p[d1]≤b.max[d1]，b.min[d2]≤p[d2]≤

b.max[d2]. 進一步，有如下引理：

引理1[15]? ?對于數據塊b中的任意本地離群點p，如果?i∈{d1，d2}，p[d1]-b.min[d1]>r且b.max[d2]-

p[d2]≥r，則數據點p是全局離群點.

對于離群點候選集中滿足引理1的數據點p，可得出其一定是全局離群點，而對于候選集中剩余的非確定的本地離群點，需和其所在數據塊的相鄰數據塊進行計算，以確定是否為真正的離群點.

定義3? ?點與數據塊的最小距離.給定數據點p和數據塊b，則點p與塊b的最小距離：

min_dist（p，b） =? ? ? （5）

其中：

z[i] = b.min[i]-p[i]，b.min[i]>p[i]

p[i]-b.max[i]，p[i]>b.max[i]

0，其他? ? ? （6）

顯然，對于塊b的近鄰塊集合N（b）中的塊bi，若min_dist（p，bi）≤r，說明塊bi中可能存在點p的近鄰，則將點p發送到Sb集合中，最終將Sb中的數據點發送到塊bi所在的處理機上. 算法3展示了具體的全局離群點計算過程.

算法3? ?全局離群點檢測算法.

輸入：數據塊b中的本地離群點集合Lb，數據塊b的近鄰塊集合

N（b），距離閾值r，數量閾值k;

輸出：本地離群點集合Lb中的全局離群點

1. FOR N（b）中的每一個數據塊bi DO

2.? ? 初始化集合Sb;

3.? ? FOR 本地離群點集合Lb中的每一個數據點p DO

4.? ? ? ?IF min_dist（p，bi）≤r THEN

5.? ? ? ? ?把數據點p加入到集合Sb中;

6.? ? ? ?ENDIF

7.? ? ENDFOR

8. 將集合Sb發送到數據塊bi所在的節點上;

9. ENDFOR

10. FOR Lb中的每個數據點p DO

11.? ? 根據各數據塊返回的結果，計算數據點p的近鄰數目 nn（p）;

12.? ? IF nn（p） < k THEN

13.? ? ? 將數據點p加入到全局離群點集合中;

14.? ? ENDIF

15. ENDFOR

復雜度分析：對于全局離群點的計算，記本地候選離群點的個數為η，根據公式（2）～（4）可將總數據集P劃分為b個數據塊，將本地候選離群點與相鄰數據塊中的數據點依次計算，因此，算法3的時間復雜度為O（η·（8/b）·|P|）. 不難發現，在分布式環境中，一個數據塊的相鄰塊通常分布在不同的處理機上，因此可以并行執行離群點的計算，使得處理效率大大提高.

6? ?實驗分析

6.1? ?實驗環境

本文實驗所搭建的異構分布式計算系統共包含5臺處理機，其中1臺主控節點，4臺從節點，它們的具體配置如下.

主控制節點：Intel Core i3-7020U CPU，4GB內存，500GB硬盤，操作系統為Windows 10;從節點1：Intel Core i5-8265U CPU，8GB內存，256GB硬盤，操作系統為Windows 10;從節點2：Intel Pentium（R） 2020M 2.4 GHz CPU，4GB內存，500GB硬盤，操作系統為Windows 10;從節點3：Intel Core i3 2100 3.1GHz CPU，8GB內存，500GB硬盤，操作系統為Windows 10;從節點4：Intel Core i3-6006U CPU，4GB內存，125GB硬盤，操作系統為Windows 10.

本文分別用真實數據集和合成數據集對所提出的GODA算法與PENL算法、BOD算法進行對比實驗.

6.2? ?真實數據集中的實驗結果分析

實驗所用的真實數據集為森林覆蓋數據集Covertype，包含581 012條數據，每條數據有10個維度，每維屬性值的范圍為[0，100]. 表4和表5展示了3種算法在該數據集中的處理時間和通信量.

如表4和表5所示，本文提出的GODA算法采用了基于網格的動態數據劃分方法GDDP，可以根據各從節點的計算能力進行數據劃分，實現異構分布式環境中各處理機的負載均衡，加快檢測效率;同時，考慮點的空間位置，將相鄰的點盡可能劃分至同一節點，大大節省了網絡開銷. 相比之下，BOD算法和PENL算法主要針對同構分布式環境，導致各節點數據分配不均衡，降低處理速度;PENL算法采用基于數據量的劃分方法，對于處理機的數據分配，都需與其他處理機上的數據集比較來確定最終結果，導致數據集重復傳輸，增加了網絡開銷.

另一方面，通過對比表4和表5中1、2行的實驗結果，可以發現，當k不變，隨著距離閾值r的增大，數據集中離群點數目逐漸減少，GODA算法和BOD算法的處理時間和通信量也逐步減少. PENL算法的處理時間與這兩種算法趨勢相同，而通信量維持不變. 這主要是因為PENL算法需要將所有處理機上的數據集進行兩兩之間的比較，網絡傳輸量與處理機的數目和數據集的規模有關，與查詢無關. 通過對比3、4行實驗結果可以看出，隨著查詢閾值k的增大，離群點的數目變多，導致GODA算法的處理時間和通信量都隨之增加. 但是，不管查詢閾值k和距離閾值r如何變化，與BOD算法和PENL算法相比，本文提出的GODA算法在異構分布式環境中能更有效地進行離群點的檢測.

6.3? ?人工合成數據集中的實驗結果分析

由于真實數據集規模有限，數據維度也無法變化，所以本節使用人工合成的數據集對3種算法進行有效性驗證. 首先，所使用的合成數據集為聚簇分布數據，各維取值范圍為0～10 000. 具體地，對于含有n個數據對象的數據集，隨機生成n/10 000個聚簇點，每個聚簇內平均包含1 000個數據對象，并以聚簇點為中心呈高斯分布. 表6給出了實驗相關變量的默認值和變化范圍.

表6? ?人工合成數據集中的參數設置

Tab.6? ?Parameter settings in a synthetic dataset

[參數 默認值 變化范圍 數據量 108 0.2 × 108 ～ 5 × 108 數據維度 10 8 ～ 16 查詢數量閾值k 50 40 ～ 60 查詢距離閾值r 16 14 ～ 18 ]

圖4描述了數據量對3種檢測算法的影響. 隨著數據量的增加，上述算法的處理時間都會變長，對應的通信量也隨之變多. 但通過對比可以發現，GODA算法和BOD算法的處理時間變化的速度較慢，而PENL算法的處理時間的增長趨勢較快，也會增大網絡開銷. 由此說明GODA算法的查詢效率要高于BOD算法和PENL算法的查詢效率.

圖5顯示了數據維度對3種算法檢測效果的影響. 在圖5（a）中，隨著數據維度的升高，PENL算法和GODA算法的處理時間呈現出線性變化，而BOD算法處理時間的增長趨勢明顯較快. 通過圖5（b）可以發現，3種算法的通信量都不受維度的影響.

圖6表述了查詢閾值k的變化對3種算法的影響. 在圖6（a）中，查詢閾值k增大時，3種算法的處理時間都變長，這是因為k增大，數據集中離群點數目增多，增加了算法的處理時間. 但與PENL算法相比，由于GODA算法和BOD算法在本地計算時良好的過濾措施，使其處理時間小于PENL算法. 通過圖6（b）可得，隨著查詢閾值k增大，PENL算法的通信量不變，而對于GODA算法和BOD算法，當k增大，使得數據集中離群點的數目增多，從而使其通信量稍微增加.

圖7描述了距離閾值r的變化對3種算法性能的影響. 在圖7（a）中，當距離閾值r不斷變大，數據集中離群點數目變少，使得所有算法的處理時間都變短. 由圖7（b）可以發現，隨著距離閾值r增大，PENL算法的通信量不變，而對于GODA算法和BOD算法，由于r變大，數據集中離群點數目減少，使其通信量也稍微變少.

通過上述對比實驗，驗證了本文提出的GODA算法的優秀性能. 與PENL算法和BOD算法相比，GODA算法可以很好地解決異構分布式環境中基于距離的離群點檢測問題.

7? ?結? ?論

本文針對常見的異構分布式環境中的離群點檢測問題，首先，提出有效的數據劃分方法GDDP，保證了各處理機計算能力的充分利用，并通過考慮數據點的空間位置信息減少網絡通信. 其次，基于GDDP方法，提出了GODA算法，在每個處理機本地，通過構建索引進行數據管理，使用過濾規則進行批量過濾，加快本地離群點計算. 再次，通過異構分布式計算框架中各節點間的網絡通信，計算出全局離群點. 最后，通過實驗驗證了GDDP和GODA算法的有效性.

參考文獻

[1]? ? KNORR E M，NG R T. Algorithms for mining distance-based outliers in large datasets[C]//Proceedings of the 24th International Conference on Very Large Data Bases. New York，USA，1998：392—403.

[2]? ? 鄭明玲，蔣句平，袁遠，等.? 一種面向大規模計算機的監控管理系統[J]. 湖南大學學報（自然科學版），2015，42（4）：107—113.

ZHENG M L，JIANG J P，YUAN Y，et al. A monitoring and management system for the large-scale computer[J].Journal of Hunan University（ Natural Sciences），2015，42（4）：107—113. （In Chinese）

[3]? ? ATKINSON A C，HAWKINS D M. Identification of outliers[J]. Biometrics，1981，37（4）：860.

[4]? ? FITRIANTO A，RANA S，MIDI H，et al. Effects of a single outlier on the coefficient of determination：An empirical study[J]. Empowering the Applications of Statistical and Mathematical Sciences，2015，1643：409—413.

[5]? ? WANG X T，SHEN D R，BAI M，et al. Cluster-based outlier detection using unsupervised extreme learning machines[C]//Proceedings of ELM-2015 Volume 1. Berlin：Springer International Publishing，2016：135—146.

[6]? ? BREUNIG M M，KRIEGEL H P，NG R T，et al. LOF：Identifying Density-Based Local Outliers[C]// Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data. Dallas，Texas，USA：ACM，2000：93—104.

[7]? ? BAY S D，SCHWABACHER M. Mining distance-based outliers in near linear time with randomization and a simple pruning rule[C]//Proceedings of the ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Texas，USA：ACM，2003：29—38.

[8]? ? YANG P，HUANG B. An efficient outlier mining algorithm for large dataset[C]// International Conference on Information Management. IEEE Computer Society，2008：41—46.

[9]? ? BUZZI-FERRARIS G ，MANENTI F . Outlier detection in large data sets[J]. Computers & Chemical Engineering，2011，35（2）：388—390.

[10]? HUNG E，CHEUNG D W. Parallel mining of outliers in large database[J]. Distributed and Parallel Databases，2002，12（1）：5—26.

[11]? BAI M，WANG X T，XIN J C，et al. An efficient algorithm for distributed density-based outlier detection on big data[J]. Neurocomputing，2016，181：19—28.

[12]? YAN Y Z，CAO L，KULHMAN C，et al. Distributed local outlier detection in big data[C]//Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Halifax，Canada，2017：1225—1234.

[13]? 王習特，申德榮，白梅，等. BOD：一種高效的分布式離群點檢測算法[J]. 計算機學報，2016，39（1）：36—51.

WANG X T，SHEN D R，BAI M，et al. BOD：An efficient algorithm for distributed outlier detection[J]. Chinese Journal of Computers，2016，39（1）：36—51. （In Chinese）

[14]? ANGIULLI F，BASTA S，LODI S，et al. GPU strategies for distance-based outlier detection[J]. IEEE Transactions on Parallel & Distributed Systems，2016，27（11）：3256—3268.

[15]? 王珊，王會舉，覃雄派，等. 架構大數據：挑戰、現狀與展望[J]. 計算機學報，2011，34（10）：1741—1752.

WANG S，WANG H J，QIN X P，et al. Architecting Big data：challenges，studies and forecasts[J]. Chinese Journal of Computers，2011，34（10）：1741—1752. （In Chinese）