基于行波效應的大跨度上承式勁性骨架拱橋抗震性能分析

賀坤龍 許偉 戶東陽 李沖杰 劉濤

（1.湖南省交通規劃勘察設計院有限公司，長沙 410000；2.中鐵二院昆明勘察設計研究院有限責任公司，昆明 650000）

橋梁作為交通工程中的樞紐結構，保證其在地震作用下的安全性非常重要。當橋梁跨徑較大時，地震波在傳播過程中經過各個支撐點時存在時間差，從而產生了行波效應［1-3］。近年來，一些學者對各類大跨度橋梁的行波效應進行研究，結果表明行波效應對結構地震響應的影響不可忽略［4-6］。趙燦輝等［7］以主跨400 m 的上承式鋼桁拱橋為例研究行波效應的影響，表明行波效應顯著增大了拱肋內力；樊珂、楊華平等［8-9］分別以主跨252 m 的上承式鋼管混凝土桁架拱橋和主跨490 m 的上承式鋼桁拱橋為例研究行波效應的影響，發現結構地震響應與行波波速之間不存在單調變化的關系。

鋼管混凝土勁性骨架拱橋剛度大、施工難度低、經濟性好，在我國西部山區高速鐵路中應用較多［10］，但其抗震方面研究較少。本文以一座高速鐵路鋼管混凝土勁性骨架拱橋為例，采用非線性時程分析方法，基于行波效應研究該橋的抗震性能。

1 工程概況及動力計算模型

1.1 工程概況

該橋主跨為340 m，矢跨比為1/4.595，拱軸線采用拱軸系數m=3.2的懸鏈線。主拱圈平面為提籃形，拱圈分叉段拱肋截面為單箱單室截面，拱圈合并段拱肋截面為單箱三室截面。拱腳基礎包括水平樁基礎和豎直樁基礎。拱上結構為3聯4跨預應力混凝土連續梁。交界墩（1#墩）和拱上立柱均采用雙柱式橋墩。左引橋為（65+65）m T構連續梁，右引橋為3跨變截面連續梁。全橋立面布置如圖1 所示，拱圈合并段單箱三室截面如圖2所示。

圖1 全橋立面布置（單位：m）

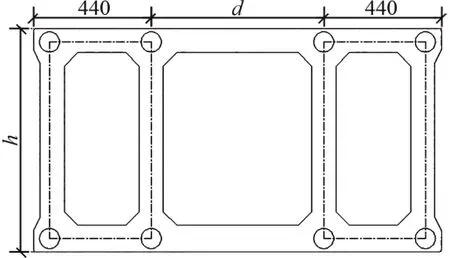
圖2 拱圈合并段單箱三室截面（單位：cm）

1.2 動力計算模型

采用有限元計算軟件建立全橋動力計算模型。除拱肋外包混凝土采用板單元模擬外，其余構件均采用梁單元模擬。拱腳水平樁基礎端部和豎向樁基礎底部采用固結。引橋橋墩墩底采用固結。拱腳水平樁基礎和豎向樁基礎均考慮樁土共同作用，并采用土彈簧模擬樁土共同作用。土彈簧剛度采用m 法計算，順橋向土彈簧剛度取7.9×108kN/m，橫橋向土彈簧剛度取8.5×108kN/m。

1.3 自振特性

動力計算方法采用多重Ritz向量法進行求解。前8階結構自振頻率和振型見表1。

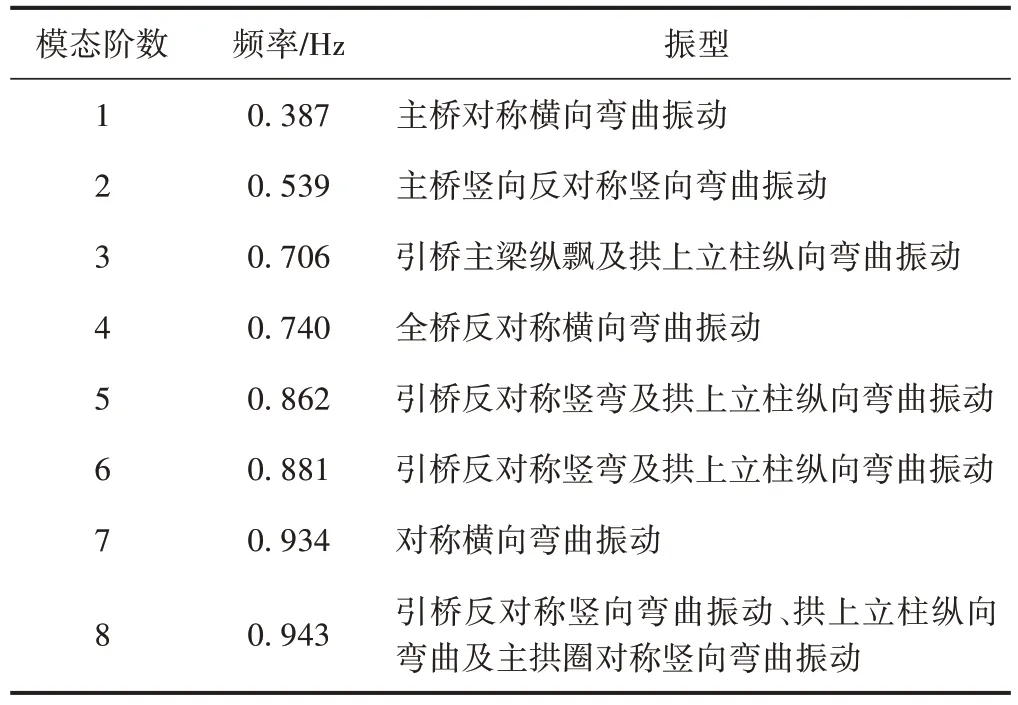
表1 全橋模型自振特性

由表1 可知，全橋模型第1 階振型為對稱橫向彎曲振動，表明其橫向剛度較弱。全橋模型基頻為0.387 Hz，屬于長周期柔性結構，這與橋梁跨度較大有關。全橋模型第3，5，6，8階出現拱上立柱縱向彎曲振動，交界墩振動表現明顯，這與其高度較高有關。

2 地震動輸入

罕遇地震作用下，基本地震動峰值加速度取0.3g，反應譜特征周期取0.45 s，對應的地震烈度為Ⅷ度。采取人工波和實錄地震波進行對比研究，人工波根據JTG/T B02-01—2008《公路橋梁抗震設計細則》中設計水平加速度反應譜擬合而成，共生成3 組人工波加速度時程曲線，地震波持時取40 s。人工波下結構地震響應取3組地震波的最大值。對比基于人工波加速度時程曲線的反應譜與設計水平加速度反應譜發現，二者吻合較好，可用于抗震時程計算分析。實錄地震波采用 1979 年 James RD. E1centro，310Deg（簡稱 James波），并對其進行調幅。地震作用方向為縱向+豎向，其中豎向地震動取縱向地震動的65%。

3 行波效應對結構地震響應的影響

3.1 拱肋內力響應分析

為了考慮波速對行波激勵下結構內力響應的影響，假定地震波從橋梁左側傳到右側，波速分別為500，1 000，2 000，3 000，4 000 m/s，計算行波激勵下拱肋關鍵位置的地震響應。在人工波一致激勵下，拱腳、1/4 拱肋、拱頂最大軸力分別為5 544，3 786，4 287 kN；拱腳、1/4拱肋、拱頂最大彎矩分別為82，69，736 kN·m。將行波激勵和一致激勵下地震響應極值的比值作為豎坐標，波速對拱肋內力的影響見圖3。

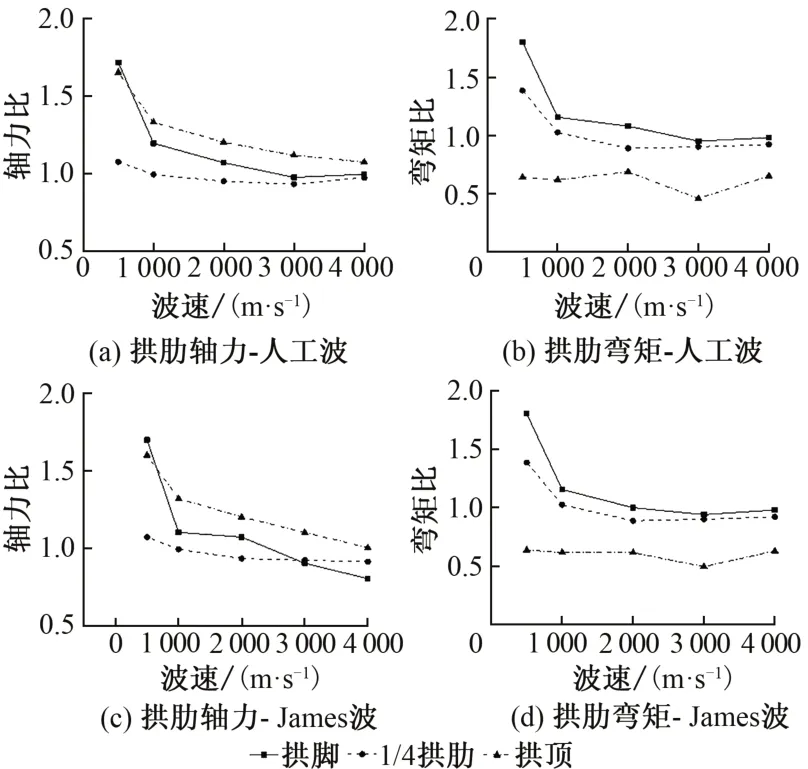
圖3 波速對拱肋內力的影響

由圖3可知：行波效應會增大拱肋的軸力，但在波速大于2 000 m/s 后，行波激勵和一致激勵產生的內力響應基本一致。行波效應會增大拱腳和1/4 拱肋的彎矩，減小拱頂的彎矩。拱肋不同位置的內力響應隨波速的變化規律基本一致，但拱腳對行波效應更加敏感。

3.2 交界墩及拱上立柱墩底內力響應分析

人工波一致激勵下1#—7#墩墩底最大彎矩分別為65 451，35 256，26 477，34 475，7 048，2 045，3 286 kN·m。波速對墩底彎矩的影響見圖4。可知：行波效應對各墩的影響規律不一致，原因是主橋空間結構復雜，振型頻率密集，當受行波激勵地震作用時，振型序列也會發生改變，導致各墩底截面的彎矩隨波速變化產生復雜的變化規律。隨著波速的增加，1#，2#和6#墩墩底最大彎矩不斷減小并趨于平緩；3#和4#墩墩底最大彎矩先減后增；5#和7#墩墩底最大彎矩變化不明顯。

3.3 交界墩及拱上立柱墩頂位移響應分析

由于1#墩高度最高，在縱向+豎向地震作用下產生的墩頂位移最大。人工波一致激勵下1#墩墩頂最大縱向位移為18 cm，墩梁最大相對縱向位移為6.6 cm。分析波速對墩頂縱向位移和墩梁相對縱向位移的影響，見圖5。

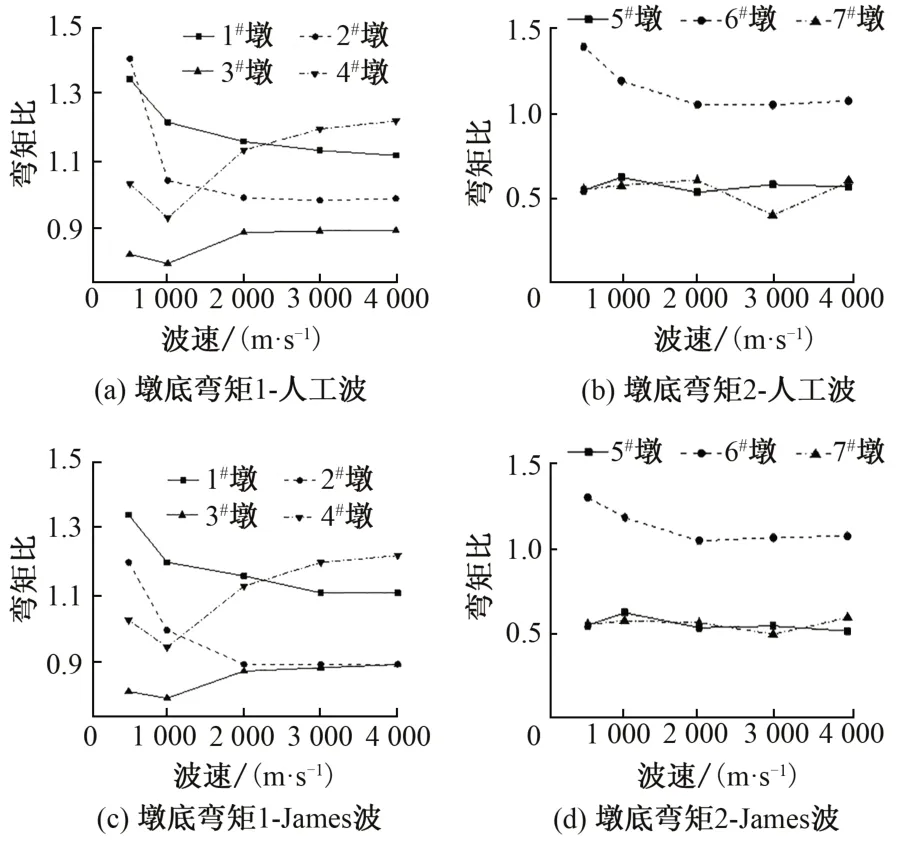
圖4 波速對墩底彎矩的影響

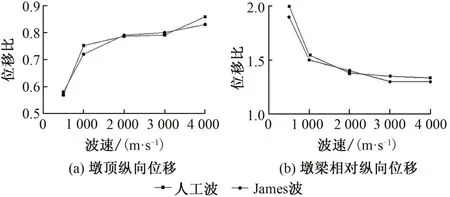
圖5 波速對墩頂縱向位移和墩梁相對縱向位移的影響

由圖5可知：人工波和James波行波效應下位移響應的規律基本一致，1#墩墩頂縱向位移小于一致激勵下墩頂縱向位移。隨著波速的增加，墩頂縱向位移逐漸變大，當波速為4 000 m/s時，其最大值為一致激勵時的86%。行波效應下墩梁相對縱向位移要大于一致激勵，且隨著波速增加，其逐漸減小并趨于平緩。

4 軟鋼阻尼器對拱橋的減震效果

4.1 軟鋼阻尼器

軟鋼阻尼器將軟鋼作為阻尼器，利用其塑性變形吸收振動能量。為防止鋼材發生受壓屈曲，通常在外側加上套筒等裝置防止內芯屈曲。日本王渡橋曾采用軟鋼阻尼器進行抗震加固并取得良好效果，本文參考該橋的布置方式，在拱橋4#立柱布置4 根軟鋼阻尼器（圖6）。支撐內芯材料采用LY100 低屈服點鋼，屈服承載力為9 000 kN，其力學本構模型采用雙線性模型（圖7）。其中，K初始和K屈服后分別為初始剛度和屈服后剛度；Xy和Xmax分別為屈服位移和極限位移；Fy和Fmax分別為屈服力和極限力。

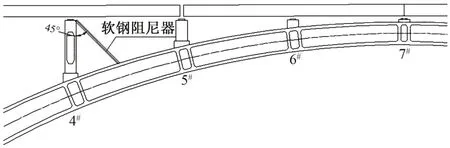
圖6 軟鋼阻尼器布置示意

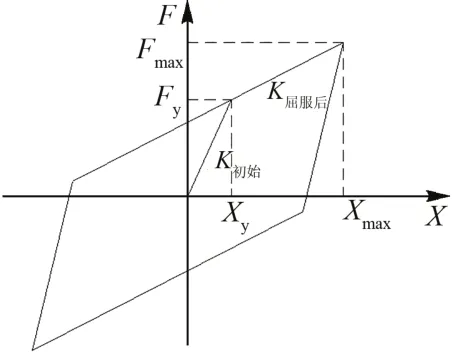
圖7 軟鋼阻尼器力學模型

4.2 減震效果分析

為評價減震效果，定義減震率=（原結構地震響應-減震結構地震響應）/原結構地震響應×100%。計算得出各拱上立柱的墩頂位移減震率和墩底彎矩減震率，見圖8。

圖8 拱上立柱墩頂位移減震率和墩底彎矩減震率

由圖8 可知：由于軟鋼阻尼器安裝在4#立柱，4#立柱減震效果明顯，墩頂位移減震率達到43.5%，墩底彎矩減震率達到60.5%；其余立柱亦有一定的減震效果。

5 結論

本文采用非線性時程法研究了大跨鋼管混凝土勁性骨架拱橋在行波效應下的抗震性能，得出以下結論：

1）該橋基頻為0.387 Hz，屬于長周期柔性結構。全橋模型第3，5，6，8 階均出現拱上立柱縱向彎曲振動，交界墩振動表現明顯，應重點關注拱上立柱及交界墩的地震響應。

2）行波效應會增大拱肋的軸力，增大拱腳和1/4拱肋的彎矩，減小拱頂的彎矩。拱肋不同位置的內力響應隨波速的變化規律基本一致，但拱腳對行波效應更加敏感。行波效應對各墩的內力影響規律不一致。行波效應會增大交界墩墩頂縱向最大位移，但會減小墩梁相對縱向最大位移。隨著波速的增加，行波效應的影響逐漸減小并趨于平緩。

3）軟鋼阻尼器對拱橋減震效果明顯，在4#立柱安裝軟鋼阻尼器，其墩頂位移減震率達到43.5%，墩底彎矩減震率達到60.5%。其余立柱的彎矩和位移均有所減小。