水溫影響下有壓水工隧洞結構穩(wěn)定分析

丁少超 王亦陳

摘?要：為解決運行期有壓引水隧洞溫度荷載和均勻內(nèi)水壓力聯(lián)合作用下的應力計算問題，采用有限元法分析隧洞運行期水溫變化所產(chǎn)生的溫度應力對襯砌應力場與應力極值的影響，通過ANSYS Workbench進行有限元分析，計算運行期不同水溫影響條件下的應力分布情況，并對比了彈性力學法計算的溫度應力極值。計算結果分析表明，在隧洞運行期混凝土水化熱基本穩(wěn)定后，水溫為溫度應力的主導條件，水溫升高會增大襯砌徑向拉應力。因此，對于夏季高溫地區(qū)或高水溫地區(qū)需調(diào)整隧洞襯砌的配筋，以適應水溫產(chǎn)生的溫度應力對隧洞襯砌結構的影響。

關鍵詞：水工隧洞;溫度場;溫度應力;應力分析; ANSYS Workbench 有限元軟件

中圖分類號：TV651?文獻標志碼：A

doi：10.3969/j.issn.1000-1379.2020.10.034

Stability Analysis of Pressurized Hydraulic Tunnel Under the Influence of Water Temperature

DING Shaochao， WANG Yichen

（Zhejiang Water Conservancy and Hydroelectric Power Consulting Center， Hangzhou 310020， China）

Abstract：Aiming at the stress calculation under the combined action of temperature load and uniform internal water pressure in the pressurized water tunnel during operation， the influence of temperature stress generated by the water temperature change during tunnel operation to the stress field and stress extreme value of the lining was analyzed by finite element method. The finite element analysis was carried out by ANSYS Workbench to calculate the stress distribution under the influence of different water temperatures during operation and compared the extreme values of temperature stress calculated by the elastic displacement harmonic method. The analysis shows that after the concrete hydration heat is basically stable during the tunnel operation period， the water temperature is the dominant condition of temperature stress， and the increase of water temperature will increase the radial tensile stress of the lining. Therefore， it is necessary to adjust the reinforcement of the tunnel lining in the summer high temperature area or high water temperature area to adapt to the influence of the temperature stress generated by the water temperature to the tunnel lining structure.

Key words： hydraulic tunnel; temperature field; temperature stress; stress analysis; ANSYS Workbench FEM software

在水工隧洞設計中，經(jīng)常遇到有壓隧洞在溫度荷載和均勻內(nèi)水壓力聯(lián)合作用下的應力計算問題[1]。近些年發(fā)展起來的抽水蓄能電站和引水式電站，其洞徑往往較大、地質(zhì)條件相對復雜、埋深較深，因此溫度應力計算問題變得更為突出。雖然國內(nèi)外對大體積混凝土工程的溫度應力研究較為重視，理論也日漸成熟，但是對于隧洞混凝土襯砌薄壁型結構的溫度應力研究較少，且沒有得到足夠的重視[2-8]，在現(xiàn)有的規(guī)范中也沒有給出相應具體溫度應力的計算方法。在實際工程中許多混凝土襯砌出現(xiàn)了由溫度應力引起的裂縫，特別是對于有壓引水隧洞，在溫度應力與內(nèi)水壓力聯(lián)合作用下引起應力疊加，使得隧洞襯砌的總應力水平提高，從而影響隧洞的安全穩(wěn)定性[9]。因此，對于有壓引水隧洞溫度應力的計算需給予重視。

筆者主要采用有限元法針對工程地質(zhì)條件復雜、圍巖等級較低、隧洞直徑較大的有壓引水隧洞進行應力分析，給出隧洞在運行期，由水溫變化所產(chǎn)生的溫度應力對襯砌應力極值的影響。

1?計算原理及方法

（1）熱傳導基本微分方程。對于圓形隧洞可將其看作均質(zhì)各向同性體[10]，采用直角坐標系（x，y，z） 時，在時刻t隧洞內(nèi)某一點的溫度為T（x，y，z，t），若采用柱坐標體系則由傅立葉熱傳導方程，可得

Tt-aSymbolQC@

2T=Wcρ;a=λcρSymbolQC@

2T=2T2r2+1rTr+2T2z2+1r2Tθ2 （1）

式中： a為導溫系數(shù);ρ為物體的密度;c為物體的比熱;λ為物體的導熱系數(shù);W為物體內(nèi)熱源強度;T為溫度;θ、r為xoy平面上投影點的極坐標;z為軸向坐標。

（2）溫度場邊界條件。對于隧洞與圍巖這兩種不同的固體接觸時，通常都假定接觸是“完全的”，即在接觸面上溫度和熱流量都是連續(xù)的[11]。邊界條件為

Ts=Tcλs（Tsn）=λc（Tcn）（2）

式中：Ts、Tc 分別為兩種介質(zhì)接觸面的溫度;λs、λc 分別為兩種介質(zhì)的導熱系數(shù);n表示法線方向。

2?有限元計算

對于水工隧洞襯砌應力的計算，傳統(tǒng)上都把襯砌看作一個獨立的研究對象，與圍巖割裂開來，僅用根據(jù)假設規(guī)律計算得來的外力代替圍巖所起的作用。有限單元法是將隧洞襯砌與圍巖看作一個整體來分析，把單位厚度的襯砌與圍巖斷面當作一個平面彈性連續(xù)體，劃分平面體為許多離散的單元，對每一單元按照其幾何與物理條件，求出節(jié)點力與節(jié)點位移。

2.1?工程概況

選取西北某水電站的有壓引水隧洞作為工程算例，隧洞全長約17.2 km，流量為260.5 m3/s，洞內(nèi)流速3.01 m/s，縱向坡比為0.19%。隧洞為圓形斷面，圍巖等級為Ⅲ、Ⅳ類圍巖，隧洞襯砌為鋼筋混凝土全斷面襯砌，洞徑為10 m，襯砌厚度為0.6 m。圍巖為花崗巖，巖石原始溫度T=12 ℃，冬季月平均最低溫度為0.2 ℃，夏季月平均最高溫度21.5 ℃。

2.2?計算方案與荷載組合

工況1：巖石壓力，襯砌自重，穩(wěn)定滲流時的地下水壓力（水頭28 m），運行期最大水壓力（水頭83 m）。

工況2：巖石壓力，襯砌自重，穩(wěn)定滲流時的地下水壓力（水頭28 m），運行期最大水壓力（水頭83 m），考慮最高水溫條件下的溫度應力。

工況3：巖石壓力，襯砌自重，穩(wěn)定滲流時的地下水壓力（水頭28 m），運行期最大水壓力（水頭83 m），考慮最低水溫條件下的溫度應力。

2.3?在ANSYS Workbench中實現(xiàn)

（1）三維建模。本例中主要采用ANSYS Workbench中的Design Modeler建立三維模型，建立的三維模型主要有覆蓋的土層、巖層、圍巖和襯砌。z軸為高程方向，頂部為地面，其他方向考慮隧洞外5倍洞徑作為圍巖邊界[12]。模型建立后將模型傳遞到Mechanical中定義各模型之間的接觸關系。

（2）網(wǎng)格劃分。在混凝土襯砌瞬態(tài)熱分析中，襯砌內(nèi)部的溫度梯度變化不大，對內(nèi)部網(wǎng)格單元要求不是很高，因此襯砌網(wǎng)格劃分時不考慮內(nèi)部網(wǎng)格尺寸的加密[12]。由于圍巖與襯砌接觸面會發(fā)生熱交換和應變，因此需要加大圍巖與襯砌接觸面上的網(wǎng)格密度。為圍巖與襯砌、襯砌與水體接觸面設置膨脹層。定義圍巖和襯砌的最小網(wǎng)格尺寸分別為1 m和0.1 m。隧洞整體有限元模型與襯砌有限元模型如圖1所示。

（3）編輯材料屬性。在ANSYS Workbench中采用結構靜力學分析時，選用非金屬材料的德魯克-普拉格（Drucke-Prager）非線性本構模型模擬圍巖和襯砌[13]。通過使用ANSYS Workbench中的參數(shù)化程序設計語言（APDL），在Mechanical中找到圍巖和襯砌模型，通過插入APDL語言來定義D-P模型。在定義圍巖與襯砌模型后，繼續(xù)添加圍巖與襯砌的物理力學參數(shù)和材料熱力學參數(shù)。對于覆蓋土層、巖層，以及混凝土材料，在分析選項中的工程數(shù)據(jù)里編輯并設置相應的物理力學參數(shù)和材料熱力學參數(shù)。

（4）設置初始條件和邊界條件。隧洞襯砌為圓形結構，其對稱面在溫度場計算中為絕熱邊界，屬于第二類熱力學邊界條件，對于襯砌外側周邊距離圍巖與襯砌接觸面較遠的為已知溫度的邊界條件。在圍巖與襯砌接觸面以及襯砌與水體接觸面，由于表面導熱系數(shù)較大，因此可將其接觸面看作光滑固體表面與空氣熱對流邊界，即第三類熱學邊界條件[14]。

溫度場初始條件：最低水溫為冬季月平均最低溫度0.2 ℃，最高水溫為夏季月平均最高溫度21.5 ℃。運行期過水后，混凝土水化熱逐漸減小，混凝土襯砌溫度基本穩(wěn)定后，襯砌外圍巖溫度恒定，其襯砌外層溫度初始值可視為恒溫[9]。依據(jù)埋入同一斷面的鋼弦式監(jiān)測儀器數(shù)據(jù)，取年平均溫度15 ℃作為初始值。

應力場邊界條件：對于水工隧洞計算區(qū)域，采取位移邊界約束。左右為水平x法向約束，底部設置彈性地基，上表面為自由面，定義圍巖與襯砌的接觸關系為綁定。為所有模型添加重力加速度方向沿z軸負方向大小為9.807 m/s2的慣性載荷，即給襯砌添加自重和上部巖石壓力與土壓力，并施加不同工況下的結構載荷，包括面壓力、靜水壓力、力矩和線壓力。

（5）分析設置。本例分析的靜力學項目有：水平位移、豎直位移、第一主應力、第三主應力、切應力、正應力。瞬態(tài)熱分析項目有：溫度場、熱流通量。

2.4?計算參數(shù)

材料力學、材料熱學計算參數(shù)見表1、表2，多年月平均水溫見表3。

3?計算結果分析

3.1?溫度場分析

工況2和工況3為隧洞運行期混凝土水化熱穩(wěn)定后，襯砌外圍巖溫度恒定。工況2為考慮7月隧洞過水時最高水溫21.5 ℃產(chǎn)生的溫度場，溫度場云圖見圖2（a），襯砌內(nèi)壁最高溫度為水溫，襯砌與圍巖接觸面溫度接近圍巖常年恒溫溫度。由圖2（b）可以看出，水溫影響下襯砌沿徑向溫度場基本成線性遞減分布，在襯砌外壁附近溫度相對穩(wěn)定。工況3為考慮1月最低水溫0.2 ℃產(chǎn)生的溫度場（見圖3），與工況2溫度場分布剛好相反，溫度沿徑向成線性遞增分布，同樣在圍巖與襯砌外壁附近溫度場較為穩(wěn)定。

3.2?應力場分析

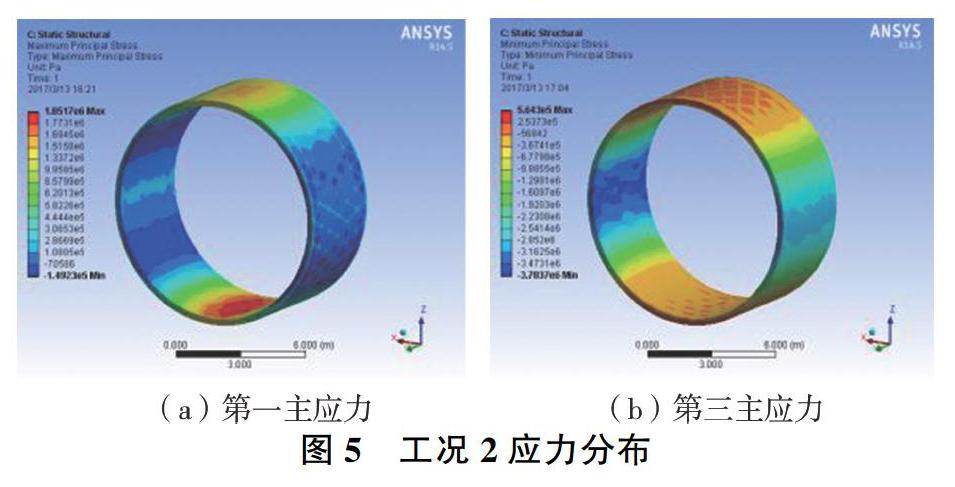
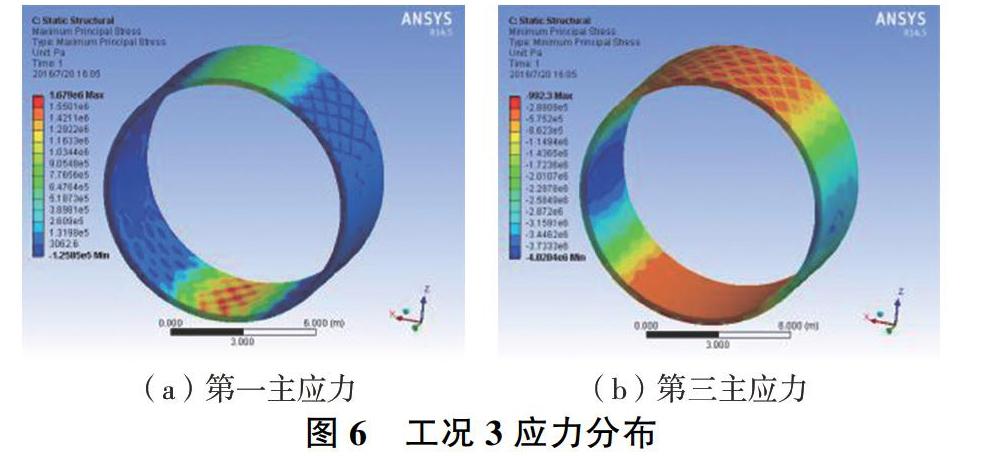
運行期增加了內(nèi)水壓力和水溫產(chǎn)生的應力場，工況1為不考慮水溫所產(chǎn)生的應力場，其最大主應力1.488 MPa，極值點出現(xiàn)在隧洞底部內(nèi)側180°位置，應力較為集中分布在底部150°～210°范圍;最小主應力-4.118 MPa，極值點出現(xiàn)在襯砌兩側90°和270°位置，應力分布見圖4。工況1的應力范圍為-4.118～1.488 MPa，可見最大拉應力超出混凝土的抗拉強度，其拉應力主要由環(huán)向鋼筋承擔。最大壓應力遠小于混凝土的抗壓強度，因此產(chǎn)生的壓應力對襯砌的影響不大。工況2應力分布見圖5，考慮了最高水溫影響的應力場，其最大主應力為1.852 MPa，最小主應力為-3.783 MPa，極值點和應力分布基本不變，應力范圍為-3.783～1.852 MPa。可見，增加高水溫的溫度應力，使襯砌的壓應力極值減小、拉應力極值增大。工況3為考慮了運行期最低水溫的影響，其最大主應力為1.678 MPa，最小主應力為-4.020 MPa，應力范圍為-4.020～1.678 MPa，最大主應力極值相對分散在拱底內(nèi)側，最小主應力分布基本不變，工況3應力分布見圖6。

3.3?變形分析

在運行期考慮襯砌內(nèi)壁受均勻內(nèi)水壓力作用和水溫影響，工況1即不計算溫度應力，水平位移極大值為1.366 1 mm，發(fā)生在襯砌兩側，豎直位移極大值為2.434 7 mm，發(fā)生在襯砌頂部，位移分布云圖見圖7;工況2即考慮夏季最高水溫影響，襯砌水平位移極大值為0.872 8 mm，豎直位移極大值為4.350 1 mm，位移分布云圖見圖8，可見高水溫時水平位移極值減小0.493 3 mm，豎直位移極值增大1.915 4 mm;工況3即考慮冬季最低水溫影響，溫度場與應力場產(chǎn)生的位移，其水平位移極大值為0.991 5 mm，豎直位移極大值為-2.834 1 mm，位移分布云圖見圖9，可見低水溫時水平位移極值減小0.374 6 mm，豎直位移極值增大0.399 4 mm。工況2與工況3相對于工況1位移極值分布的位置基本保持一致。

3.4?應力分析總結

對比工況1、工況2、工況3可知，運行期混凝土水化熱基本穩(wěn)定后，水溫成為溫度應力的主導條件，隧洞運行期水溫主要產(chǎn)生徑向拉應力，高水溫比低水溫產(chǎn)生的拉應力大。因此，在一些夏季高溫地區(qū)或高水溫地區(qū)需調(diào)整隧洞襯砌的配筋，以適應水溫產(chǎn)生的溫度應力對隧洞襯砌結構的影響。應力分析成果見表4。圖7?工況1位移分布云圖

4?對比分析

按照《水工隧洞設計規(guī)范》（DL/T 5195—2004）有壓圓形隧洞襯砌各應力系數(shù)表[15]，通過有限元法分析可知應力極值位置出現(xiàn)在隧洞底部與兩側，因此在計算隧洞斷面時選擇90°和180°斷面。表5為彈性力學法計算出的各工況應力組合下極值情況，根據(jù)表6對比有限元法和彈性力學法計算的應力極值情況可以看出兩種方法大致相近。從應力極值分布情況來看，彈性力學法與有限元法計算的壓應力極值都出現(xiàn)在襯砌與圍巖接觸面上，拉應力極值均出現(xiàn)在襯砌內(nèi)邊緣。彈性力學法計算出工況2拉應力最大值為2.533 MPa，工況3出現(xiàn)最大壓應力值為5.079 MPa，有限元法計算出工況2拉應力最大值為1.852 MPa，工況1出現(xiàn)最大壓應力為4.118 MPa。可以看出彈性力學法計算的拉應力和壓應力極值相對偏大，原因是彈性力學法對荷載之間的相互作用以及圍巖、襯砌的材料性質(zhì)之間的相互影響考慮不足。

5?結?論

（1）運行期考慮內(nèi)水壓力的情況下，溫度應力對襯砌的整體變形影響較小。最低水溫相對于最高水溫水平位移增大了0.118 7 mm，垂直位移減小了1.156 0 mm，可知高水溫相對于低水溫對襯砌的結構穩(wěn)定更加不利。

（2）運行期增加內(nèi)水壓力使得襯砌的最大主應力、最小主應力、切應力和正應力都相應增大。拉應力極值超出了混凝土抗拉強度，壓應力極值增大但仍小于混凝土軸心抗壓強度標準值。可知，有壓引水隧洞只使用混凝土襯砌達不到抗拉強度的要求，需根據(jù)計算的應力極值來決定襯砌類型。

（3）運行期混凝土水化熱基本穩(wěn)定后，水溫則成為溫度應力的主導條件，隧洞運行期水溫主要產(chǎn)生徑向拉應力，高水溫比低水溫產(chǎn)生的拉應力大，高水溫相對于低水溫對襯砌的結構穩(wěn)定更加不利。因此，在一些夏季高溫地區(qū)或高水溫地區(qū)需調(diào)整隧洞襯砌的配筋，以適應水溫產(chǎn)生的溫度應力對隧洞襯砌結構的影響。

參考文獻：

[1]?汪胡楨.水工隧洞的設計理論和計算[M].北京：水利電力出版社，1990：77.

[2]?ROHOLA H， JAMAI R， BAHTIYAR U. 3D Finite Difference Kodel for Simulation of Double Shield TBM Tunnelling in Squeezing Grounds[J]. Tunnelling and Underground Space Technology， 2014， 40： 109-126.

[3]?KARGAR A R， RAHMANNEJAD R， HAJABASI M A. The Stress State Around Lined Non-Circular Hydraulic Tunnels Below the Water Table Using Complex Variable Method[J]. International Journal of Rock Mechanics & Mining Sciences， 2015， 78：207-216.

[4]?ZHONG D H， HU N， CHENG Z F. 3D Finite Element Analysis of TBM Water Diversion Tunnel Segment Coupled with Seepage Field[J]. Transactions of Tianjin University，2016， 22：35-42.

[5]?王克忠，唐雨薔，李偉平，等.滲流-應力耦合下深埋引水隧洞變形穩(wěn)定性分析[J].浙江工業(yè)大學學報，2016， 44（2）：207-211.

[6]?蘇凱，伍鶴皋.水工隧洞鋼筋混凝土襯砌非線性有限元分析[J].巖土力學， 2005，26（9）：1485-1490.

[7]?邵潮鑫，沈振中.基于ANSYS的隧洞襯砌有限元分析配筋法研究[J].南水北調(diào)與水利科技，2014， 12（4）：116-119.

[8]?董正中，肖明，楊瑩.復雜隧洞襯砌結構的三維有限元分析及結構配筋[J].中國農(nóng)村水利水電，2016（1）：109-113.

[9]?蔡曉鴻，蔡勇平.水工壓力隧洞結構應力計算[M]. 北京：中國水利水電出版社，2004：165.

[10]?宿輝，馬超豪，馬飛.基于高地溫引水隧洞的溫度場數(shù)值模擬研究[J].水利水電技術，2016，47（7）：34-37.

[11]?ZHOU X， ZENG Y， FAN L. Temperature Field Analysis of a Cold-Region Railway Tunnel Considering Mechanical and Train-Induced Ventilation Effects[J]. Applied Thermal Engineering， 2016， 100：114-124.

[12]?WU D， ZHANG Y， ZHAO R， et al. A Coupled Thermal-Hydraulic-Mechanical Application for Subway Tunnel[J]. Computers & Geotechnics， 2017， 84：174-182.

[13]?SONG F， XU Y， HAN C， et al. 3D Simulation and Analysis on Effect of Construction Process of Urban Shallow Tunnel[J]. Chinese Journal of Underground Space & Engineering， 2013， 9（1）：141-146.

[14]?WANG W， LU C F， LI Y X. Effects of Stress and High Temperature on the Carbonation Resistance of Fly Ash Concrete[J]. Construction and Building Materials，2017，138：486-495.

[15]?中華人民共和國國家發(fā)展和改革委員會. 水工隧洞設計規(guī)范：DL/T 5195—2004[S]. 北京：中國電力出版社，2004：68-69.

【責任編輯?趙宏偉】