雙筋矩形梁正截面受彎承載力計算方法的合理分析

曹鋒 張仁苓

摘要：根據雙筋矩形梁正截面受彎承載力的計算原理，針對受壓區配筋已知，求受拉區配筋的情況，介紹了三種雙筋矩形梁正截面受彎承載力的計算方法：解方程法、截面分解法、綜合求解法。闡述了三種計算方法的適用條件以及求解過程，并分析了三種計算方法的合理性及準確性。通過工程算例分析，得到三種計算方法求解結果的差異性，以及對配筋設計的影響。隨著混凝土強度等級提高及構件截面高度增加，進一步分析三種計算方法的合理性及配筋情況變化規律，三種計算方法結果基本一致。

關鍵詞：雙筋矩形梁;受彎承載力;計算方法;配筋設計

中圖分類號：TU311.4

文獻標志碼：A

1雙筋矩形梁正截面受彎承載力計算原理

1.1計算公式

雙筋矩形梁的配筋設計有兩種情況，一種是兩側鋼筋均未知;一種是因為構造等原因，已知受壓區鋼筋，求受拉區鋼筋[1]。雙筋矩形截面受彎構件正截面受彎承載力計算簡圖如圖1所示[2]。

由力的平衡條件可得：

a1fcbx+f'yA's=fyAs

（1）

由力矩平衡條件可得：

Mu=a1fcbx（h0-x/2）+f'yA's（h0-a's）

（2）

其巾：a1為混凝土受壓區等效矩形應力圖系數，fc為混凝土軸心抗壓強度設計值，x為混凝土受壓區高度，f'y鋼筋抗壓強度設計值，fy為鋼筋抗拉強度設計值，A's為受壓區鋼筋截面面積，As為受拉區鋼筋截面面積，Mu為正截面受彎承載力。

當受壓區配筋已知，求受拉區配筋面積時，上述方程組中有兩個未知數x和A's，對上述方程組進行求解。

由（2）式可得：

A's=M-a1fcbx（h0-x/2）/f'y（h0-a's）

（3）

由（1）式可得：

As=A's+a1fcbx/fy

（4）

1.2適用條件

應用以上二式時，必須滿足以下適用條件[3-4]：

（1） X≤ξbh0，防止受壓區混凝土在受拉鋼筋屈服前壓碎;

（2）x≥2a's：，保證受壓鋼筋在受壓區混凝土壓碎前屈服。

2計算方法

2.1解方程法

由（2）式求解一元二次方程得：

M-fy4。（矗。

x=h0-，再將x代入上述（4）式，即可求出As。

2.2截面分解法

如圖所示，把圖1的雙筋矩形截面分解為以下兩個截面相加：一個截面是由受壓鋼筋As與對應的部分受拉鋼筋As1構成的，提供承載力Mu1;另一個截面是由剩余部分受拉鋼筋As2和受壓區混凝土組成的單筋矩形截面，提供承載力Mu2[5];如圖2所示。

由截面I可得：

fyAS1=fy'As'

（5）

Mu1=fy'As'（h0-as'）

（6）

由截面Ⅱ可得：

fyAs2=a1fcbx

（7）

Mu2=a1fcbx（h0-x/2）

（8）

根據截面I受力情況，由（5）可得As1=As'，由（6）式可求出Mu1，則Mu2=Mu-Mu1。根據截面Ⅱ受力圖示及（7）式、（8）式，截面Ⅱ為單筋矩形截面，即可求出x和As2，最終配筋面積As=As1+As2。

2.3綜合求解法

將前述（3）式代入（4）式可得：

As=M+a1fcbx（x/2-as'）/fy（h0-as'）

（9）

再由前述解方程法求得x，代入（9）式，求出As。

2.4實例及應用

取一雙筋矩形截面梁，截面高度為500 mm，寬度為200mm，混凝土為C40，鋼筋為HRB400，梁上作用彎矩設計值M=330KN·m.一類環境，在受壓區已配置縱向受力鋼筋320，As'=941mm2。求受拉鋼筋截面面積As。

（1）解方程法

x=h0-

=435-

=140.88mm>2as=80mm

As=α1fcbx+fy'As'/fy=360×941+1.0×19.1×200×140.88/360

= 2435.87mm2

（2）截面分解法

Mu1=fy'As'（h0-as'）=360×941×（435-40）

=133.81×106N·mm

Mu1=M-Mu1=330x106-133.81×106

=196.19×106N·mm

αs=Mu2/α1fcbh02=196.19×106/1.0×19.1×200×4352=0.272

rs=0.5（1+√1-2αs）=0.5（1+√1-2×0.272）=0.838

As=Mu2/fyrsh0=196.19×106/360×0.838×435=1495mm2

As=As1+As2=941+1495=2436mm2

（3）綜合求解法

As=M+α1fcbx（x/2-as'）/fy（h0-as'）

=330×106+1.0×19.1×200×140.88×（140.88/2-40）/360×（435-40）

= 2435.88mm2

同一工程實例，采用上述三種計算方法所得結果極為接近，根據計算結果，均可選配鋼筋為525，As=2454mm2，配筋滿足要求。

3計算方法分析

3.1混凝土強度影響

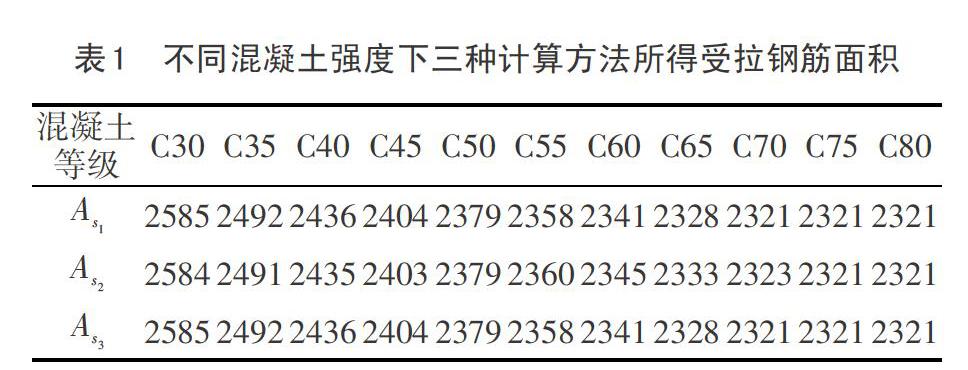
對上述計算實例，截面尺寸、鋼筋強度等級及梁截面所受彎矩作用不變條件下，改變混凝土強度等級，分別按上述三種計算方法求得其受拉鋼筋配筋面積，計算結果統計于表1，表中As1為按照解方程法（方法一）計算的配筋面積，As2為按照截面分解法（方法二）計算的配筋面積，As3為按照綜合求解法（方法三）計算的配筋面積[6]。

將表1的計算結果繪制于圖3，可得雙筋矩形梁受拉區配筋面積隨著混凝土強度等級變化的關系曲線，如圖3所示。

由圖3可知，隨著混凝土強度等級的提高，雙筋矩形截面受拉鋼筋的配筋面積不斷減小，且用三種計算方法求得的受拉鋼筋面積變化規律相同，均隨混凝土強度的提高逐漸減小，前期減小較快，后期逐漸變緩。但是減小的幅度較小，即提高混凝土強度雙筋矩形截面配筋面積影響較小。三種計算方法所得的計算結果十分接近，則三種計算方法均較為合理。

3.2截面高度影響

對上述計算實例，當材料強度等級、截面寬度及所受彎矩不變的情況下，改變截面高度，分別按上述三種計算方法分別求得其受拉鋼筋配筋面積，計算結果統計于表2。

將表2的計算結果繪制成圖，可得鋼筋混凝土受彎構件配筋率隨著梁截面高度的變化關系曲線，如圖4所示。

由圖4得知，隨著構件截面高度的增加，雙筋矩形截面受拉鋼筋的配筋面積不斷減小，且三種計算方法求得的受拉鋼筋面積變化規律相同，受拉鋼筋面積減小的幅度較大，即增加梁截面高度對雙筋矩形截面配筋面積的影響較大。三種計算方法所得的計算結果十分接近，則三種計算方法均較為合理。

4結論

（1）鋼筋混凝土受彎構件正截面受彎承載力的計算方法，可采用一元二次方程法、截面法、簡易法，三種方法的計算結果十分接近。一元二次方程法計算過程簡單，但求解較難;簡易法和一元二次方程求解有相似之處;而截面法是一種比較新穎的并且使用了單筋截面的解法;因此，建議選用截面法求解。

（2）隨著混凝土強度等級的提高，受拉鋼筋配筋面積呈減小趨勢，但是減小的幅度較小，且三種計算方法求得的配筋面積基本相同，提高混凝土強度等級對雙筋截面受彎構件配筋率影響不大。

（3）隨著構件截面高度的增加，受拉鋼筋配筋面積呈減小趨勢，減小的幅度較大，且三種計算方法求得的配筋面積也基本相同，增加梁截面高度對鋼筋混凝土受彎構件配筋率影響較大。

參考文獻：

[1]東南大學，天津大學，同濟大學.混凝土結構設計原理[M].北京：中圍建筑工業出版社，2018.

[2]中華人民共和圍住房和城鄉建設部.混凝土結構設計規范：GB50010-2010[S].北京：中國建筑工業出版社，2015.

[3]曹鋒，陳夢霞，陳志遠，等.雙筋矩形RC梁配筋設計影響因素及變化規律研究[J].佳木斯大學學報（自然科學版），2020，38（2）：20-23.

[4]陳小英，朱浪濤.鋼筋混凝土構件正截面承載力計算公式的教學探討[J].高等建筑教育，2018，27（4）：100-105.

[5]曹鋒.鋼筋混凝土受彎構件正截面受彎承載力計算方法的合理分析[J].甘肅科技縱橫，2019，48（4）：35-37，58.

[6]高麗，王勇.受彎構件正截面承載力若干問題探討[J].山西建筑，2017，43（6）：43-44.

收稿日期：2020-06-11

基金項目：青海民族大學建筑與結構教研創新團隊項目（項目編號：2019-JYTD-002）。

作者簡介：曹鋒（1989-），男，漢族，陜西商洛人，碩士，講師，主要從事建筑與土木工程方向的教學與研究工作。