針栓式噴注單元霧化角模型分析
王凱,雷凡培,張波濤,楊岸龍,周立新
1.西安航天動力研究所 液體火箭發動機技術重點實驗室,西安 710100 2.中國船舶工業集團有限公司,北京 100044
近年來隨著商業航天的迅猛發展,特別是SpaceX等商業航天公司的迅速崛起,國內外掀起了高性能、長壽命可重復使用、低成本、推力深度可調的液體火箭發動機技術研究的熱潮。在變推力液體火箭發動機設計中,噴注器的設計尤為重要。與雙組元液體火箭發動機上常用的典型撞擊式或同軸式噴嘴比較,針栓式噴注器具有獨特的幾何特性和噴注特性,變推力工況下能夠產生很高的燃燒效率(典型值為96%~99%),并具有調節能力強、面關機、操作安全、固有燃燒穩定性好等工作特性[1]。另外,針栓式噴注器可以在很寬的推力水平內按比例放大或縮小,并可適應不同的推進劑組合,不用設置諸如聲腔或隔板之類的穩定裝置。相比傳統火箭發動機的噴注器由成百上千個精細的噴嘴組成,針栓式噴注器的結構大為簡化,意味著可靠性提高,同時可以快速更換零組件實現改進升級[2],減少質量和降低成本。這些工作特性給火箭發動機的設計、性能、穩定性和試驗靈活性帶來了極大的好處,也被看成是降低現有運載器大發動機成本的一種有效手段。
針栓式噴注器典型的工作原理是通過伸入燃燒室內部的針栓結構,使一種推進劑流經針栓中心流道,并由針栓頭端附近的一系列孔(或縫隙)呈放射狀徑向噴注;另一種推進劑通過針栓外側的環形縫隙軸向噴注,兩者呈90°交叉撞擊,使推進劑霧化混合[3],具體原理結構如圖1所示。針栓式噴注器的概念最早出現于20世紀50年代噴氣推進實驗室(Jet Propulsion Laboratory,JPL)設計的一種簡單而精致的試驗裝置。后來1960年TRW公司開始實踐和研制針栓式噴注器,其后的 40年間,至少有60多種方案進行了熱試車[4]。最著名的針栓式發動機為阿波羅登月艙下降發動機LMDE,其采用N2O4/A-50,推力變比10∶1 (4.67~ 46.7 kN)[5-6]。從20世紀80年代開始,TRW又對針栓式噴注器進行了一系列設計改進,實現了噴注面關機及凝膠推進劑的成功應用。從20世紀90年代開始,在進一步提升常規推進劑針栓式發動機性能的同時,重點開展了液氧/液氫[7-8]、液氧/煤油[9]、液氧/甲烷[10-11]等針栓式發動機研究,在低溫推進劑應用、低成本方案、按比例放大設計上取得了顯著的成果,并將其應用于大推力針栓式發動機的研制。如2 900 kN的TR106 LOX/LH2發動機[12-15],SpaceX的Merlin 1D系列發動機[16-17]。

圖1 針栓式噴注器原理圖Fig.1 Schematic diagram of pintle injector
中國對針栓式變推力發動機的研究主要從20世紀70年代開始,在2013年中國研制的5∶1月球探測用7 500 N針栓式發動機成功將嫦娥CE-3送到了月球表面,2019年又將CE-4首次送到月球背面。為了實現載人登月,中國也開展了用于登月艙下降的液氧/甲烷針栓式變推力發動機方案研究[18]。經過幾十年的研究,中國已經基本掌握了針栓式發動機的設計技術,然而與工程研制的輝煌成就相比,針栓式噴注器工作特性的理論研究尚不足,許多機理尚不清楚。因此需要針對一些關鍵結構和工作參數進行系統深入的研究。
前期關于針栓式噴注器的研究主要集中在TRW公司,主要依靠大量試驗數據和豐富的設計經驗。他們的研究發現除了針栓式噴注器單元的幾何尺寸參數外,重點關注的無量綱參數有動量比CTMR和阻塞率CBF,噴注特性參數有噴注速度和霧化角θ。

針栓式噴注器結構形式獨特,霧場范圍大,過于稠密,光學觀測困難,現有光學測量設備較難獲得有效噴霧場參數,為了解決此問題,Sakaki等率先提出平面針栓式噴注器單元的設想,選取最小噴注單元為研究對象,研究了動量比和噴霧場結構的關系,結果表明平面針栓與軸對稱針栓的特性基本一致[31-32]。
以前研究者的結果均是液膜/液膜撞擊,屬于二維平面撞擊,而實際的液液針栓式噴注器一般都是液膜/液束撞擊,屬于三維空間撞擊,撞擊過程中液膜液束均會發生顯著變形,流場結構更加復雜,此時霧化角與動量比的關系存在較大差異,阻塞率及徑向孔的形狀也成為影響霧化角的重要參數。目前仍未見報道關于液膜撞擊液束的基礎理論分析和定量研究,其有待于進一步研究。因此,本文以平面針栓噴注單元為研究對象,首先通過理論推導引入了變形因子,將撞擊的幾何變形效應與霧化角關聯,建立液膜/液膜撞擊霧化角模型;接著通過引入阻塞率定義有效撞擊動量比,同時將液膜/液束撞擊變形的影響隱含考慮在變形因子中,建立液膜/液束撞擊霧化角模型;并與常用霧化角模型進行對比分析,揭示霧化角模型之間的本質區別;然后通過數值仿真和試驗結果對霧化角模型進行驗證;最后針對圓孔液束與液膜相互作用,建立了對應的變形因子組合系數,獲得適應性更廣、準確性更高的霧化角預測模型。
1 霧化角理論模型分析
1.1 液膜/液膜撞擊霧化角模型
1.1.1 基本定義
下面通過動量比的定義分析Boettcher等[20]的研究結果中二維平面膜與三維環形膜霧化角差異的原因。兩種結構的膜撞擊示意圖如圖2所示。

圖2 液膜撞擊液膜示意圖Fig.2 Schematic diagram of one liquid sheet impacting another liquid sheet
對于平面膜,動量比為
(1)
對于環形膜,動量比為
(2)
式(1)~式(2)中:Ap,1和Ap,2分別為二維平面膜的軸向路和徑向路流通面積;ρ1和ρ2分別為軸向和徑向流體密度;A1和A2分別為軸向和徑向流通橫截面積;h1和h2分別為軸向和徑向液膜厚度;D為針栓柱直徑。

1.1.2 基本假設
根據撞擊物理過程建立如圖3所示的控制體幾何模型,做出以下假設:

圖3 控制體幾何模型Fig.3 Geometric model for control body
1) 兩種液體不相溶。
2) 流動過程是穩態,即流動與時間無關。
3) 入口和出口截面的速度方向垂直于該截面。
4) 假定控制體1的入口和2個控制體的出口均遠離撞擊點,因此這些面的壓力均可視為環境壓力。
5) 忽略體積力(如重力等)和表面張力。
6) 忽略壁面對液膜的摩擦阻力和環境氣體對氣液自由表面的剪切阻力。
7) 不考慮相間傳熱和相變(如蒸發)。
8) 軸向動量守恒,徑向動量不守恒[33]。
1.1.3 霧化角公式推導
由忽略非穩態項和體積力的積分型動量方程可得
∮AV(ρV·dA)+∮ApdA=Fs
(3)
式中:V為速度矢量;A為面積;A為控制體表面矢量;ρ為流體密度;p為壓力;Fs為相界面間剪切阻力。
根據假設,將式(3)應用于控制體1和控制體2,得到相應的動量方程在軸向(z方向)的投影方程為

(4)
式中:V為速度大小;下標1和2分別表示控制體1和2;下標in和out分別表示入口和出口截面。
從式(4)可見,2種液相界面間的壓力和剪切阻力屬于內力(作用力與反作用力),求和為零,故式(4)未出現此項。式(4)主要根據重要假設(8)獲得,假設(8)在文獻[33]中有詳細的論證過程,并已得到了試驗及數值仿真結果的充分驗證。
從式(4)可獲得霧化角為

(5)
式(5)與Cheng等[30]得到的方程相同,然而推導過程不同,接下來的推導過程則導致最終結果與其不同。

將上述定義的參數代入式(5)可得
(6)



(7)

(8)
式(8)中C1和C2分別是2個控制體入口截面的面積與撞擊后出口截面的面積之比,物理意義是表征由于撞擊造成的截面面積變化。通過引入變形因子C1和C2將撞擊的幾何變形效應與霧化角關聯,同時也可將撞擊液膜的幾何形狀因素考慮其中,從而可以更加準確地描述霧化角與影響因素之間的關系。
1.2 液膜/液束撞擊霧化角模型

(9)
式中:A1in total為軸向環縫液膜流動截面的總面積。式(9)中隱含假設認為w=d。
以單個液膜/液束撞擊單元作為控制體研究對象,如圖4所示,基于液膜撞擊液膜的霧化角分析模型,將式(9)代入式(8)中可推導出液膜撞擊液束的霧化角模型為

圖4 液膜/液束撞擊單元Fig.4 Injection element of liquid sheet impacting liquid jet
(10)
液膜/液束撞擊過程中液束會同時發生彎曲變形和橫截面變形,液膜也會發生繞液束流動,因此液膜/液束撞擊后截面面積會發生較大變化,通過在式(10)中引入變形因子C1和C2,隱含考慮了液膜/液束撞擊的顯著影響,進而修正了霧化角模型。與液膜/液膜撞擊相比,液膜/液束撞擊的一個顯著不同是液束的入口孔型有多種選擇,可以是單一孔型(如圓孔、橢圓孔、方孔、長寬比不同的矩形槽等),也可以是以上各種形狀的組合孔型,這些不同形狀的液束與液膜發生撞擊后,霧化角變化規律類似,可通過相應的變形因子C1和C2的組合系數來表征,從而描述不同孔型液束與液膜撞擊的相互作用,進而獲得適應不同情況更加準確的液膜撞擊液束的霧化角模型。本文中主要以簡單的圓孔為例開展研究。
1.3 模型分析討論
關于霧化角公式(8)的討論:
1) 由于推導過程中以守恒量ρV2整體進行積分變換,后面又引入了平均密度,因此式(8)既適用于不可壓的液體膜及氣體膜撞擊,也適用于可壓縮的氣體膜撞擊。
2) 當認為兩路液體撞擊后出口截面面積與各自入口截面面積相等時,式(8)中2個變形因子均等于1,因此霧化角公式簡化為
(11)
式(11)與Cheng等[30]得到的結果一致,從而也可以看出Cheng等[30]的結果僅適用于2個變形因子均為1的特殊情況,這也正是引入變形因子的新模型與Cheng模型的不同之處。對于二維平面膜撞擊,各自的截面積變化相對小,變形因子均為1的假設近似成立。對于液膜/液束撞擊,液膜繞流變形和液束變形效應更顯著,變形因子更容易偏離1。具體的變形因子數值可根據不同的撞擊形式及幾何形狀,通過試驗和數值仿真獲取,進而可獲得適應性更廣、準確性更高的霧化角預估模型。
3) 從式(5)或式(6)不難看出,該模型的霧化角余弦值等于軸向入口動量(即控制體1的入口截面動量)與撞擊后出口總動量(即控制體1和2的出口截面的動量和)之比,是根據實際的出口軸向動量(等于入口軸向動量)和出口合成總動量來計算霧化角,隱含考慮了撞擊造成的影響,也適合引入撞擊液膜與液束的幾何形狀因素。該模型僅認為軸向動量守恒,徑向動量不守恒。而相比于另一種常用的霧化角模型:tanθ=CTMR,即
(12)
該常用模型的霧化角余弦值等于軸向入口動量與撞擊前入口合成總動量(即軸向入口動量與徑向入口動量平方和的算術平方根)之比,是根據撞擊前入口的軸向動量和合成總動量來計算霧化角,未考慮撞擊造成的影響,成立的前提條件是動量完全守恒(軸向動量守恒和徑向動量守恒),這也是式(12)和式(8)2個霧化角模型的本質區別。

2 數值物理模型
2.1 數值方法
2.1.1 控制方程
數值仿真采用開源軟件Gerris作為計算工具。Gerris采用的數值方法Popinet在文獻[34-35]中作了詳細的描述,下面對Gerris采用的數值方法做一個總結性的描述。Gerris求解的是不可壓、變密度、帶有表面張力的Navier-Stokes方程[34-35]。
(13)

采用氣相、液相1和液相2三相進行計算,分別定義液相1體積分數c1(x,t)和液相2體積分數c2(x,t),得到的流體密度和黏性系數為
(14)
式中:ρl1、ρl2和μl1、μl2分別是液相1和液相2的密度和黏度;ρg和μg分別為氣相的密度和黏度。
在Gerris中使用經典的時間分裂投影法進行簡化,達到時間二階精度。使用四叉樹/八叉樹進行空間離散,達到空間二階精度,使得自適應加密算法(根據流場參數變化對局部網格進行動態加密或粗化)可簡易靈活地實現,在不損失計算精度的情況下顯著降低了計算量,非常適合處理多尺度流動問題。使用分段線性的VOF(Volume of Fluid)幾何重構方法進行自適應網格界面捕捉,該方法非常適合應用于包含破碎、聚合現象的霧化過程計算[36-38],如圖5所示為計算生成的自適應網格。通過將表面張力轉化為某一區域連續的體積力并結合高度函數曲率估計實現表面張力的精確求解。采用單調集成大渦模擬(MILES)(又稱隱式大渦模擬(ILES))[39]近似模擬亞格子(SGS)的能量傳遞,這是由于數值計算不可避免地有數值耗散。

圖5 基于分段線性VOF幾何重構方法的自適應網格加密Fig.5 Adaptive mesh refinement based on a piecewise-linear geometrical VOF
2.1.2 氣液相界面捕捉
VOF方法通過定義體積分數函數c來描述界面(含有運動界面的網格滿足0 采用分段線性的VOF方法(Piecewise-Linear Interface Calculation VOF,PLIC VOF)對界面進行重構,圖6所示紅色斜平面描述的是不同情況下的相界面,其中網格單元為單位長度的正方體,相界面的單位法向量n由液相一側指向氣相一側,α為相界面斜平面和原點之間的最小距離,液相的體積分數c(體積)可由n和α唯一確定表達,H(x)為Heaviside階躍函數。 圖6 分段線性的VOF界面重構方法Fig.6 Piecewise-linear VOF interface reconstruction method 計算所選用的結構參數及計算域如圖7所示,軸向液膜厚度為h1,軸向速度為u1,徑向液膜厚度(或液束直徑)為h2(或d),徑向速度為u2。圖7(a)為二維軸對稱液膜撞擊液膜的模型,計算域由8個L×L的基本結構Box構成,左端面和底端面為軸向液膜和徑向液膜入口;圖7(b)為液膜撞擊液束的模型,計算域由8個L×L×L的基本結構Box構成,計算域左端面和底端面分別為軸向液膜和徑向液束入口,液膜展向寬度取10 mm。圖中標注的面為無滑移壁面,其余面為出口,采用Outflow邊界,背壓為大氣環境。第1相為空氣,第2相和第3相均為水。計算域的L= 10 mm,最高網格等級采用Level=9加密,最小網格約19.5 μm。網格自適應函數設置為體積分數梯度,即網格會實時根據流場中計算的體積分數梯度大小進行自適應加密或粗化。設定軸向液膜與徑向液膜或液束撞擊前的距離(即跳躍距離)為6 mm,對應模擬的針栓柱直徑D=20 mm,其他具體的工況參數詳見表1~表4。數值仿真獲得霧化角的結果如圖8所示。 圖7 計算域示意圖Fig.7 Sketch map of computation zone 表1 液膜撞擊液膜的結構參數表Table 1 Structural parameters of different injectors with liquid sheet impinging on liquid sheet 表2 液膜撞擊液膜的工況參數表Table 2 Working parameters of different injectors with liquid sheet impinging on liquid sheet 表3 液膜撞擊液束的結構參數表Table 3 Structural parameters of different injectors with liquid sheet impinging on liquid jet 表4 液膜撞擊液膜的工況參數表Table 4 Working parameters of different injectors with liquid sheet impinging on liquid jet 圖8 數值仿真獲得的霧化角Fig.8 Spray angle of numerical simulation 為了深入研究不同幾何結構參數、流動工況參數在大范圍變化情況下對霧化角的影響規律,同時便于開展有效光學觀測及將試驗結果與數值仿真結果進行對比,冷態試驗的噴注器設計借用文獻[31-32]中平面針栓式噴注單元的設計理念,采用噴注器單元結構可更換的方案設計了平面針栓式噴注單元試驗裝置。平面針栓式噴注單元由一個可更換的液膜生成構件和一個可更換的液束生成構件組成,試驗件如圖9所示。液膜生成構件可以產生一定厚度的平面液膜,平面液膜的寬度足夠寬,設計中單孔噴注單元選取液膜寬度為10 mm;液束生成構件可以產生一定孔型型面和一定尺寸的射流。試驗中液膜和液束兩路單獨供應,通過分別改變液膜和液束兩路流量及更換不同結構尺寸的液膜和液束構件,從而形成不同動量比的工況。 圖9 液液平面針栓式噴注單元試驗件結構Fig.9 Structure of liquid-liquid plane pintle injector element 為了充分研究無量綱參數動量比的影響,方案中工況設計選取的動量比從0.1到6.25,覆蓋較寬的變化范圍;同時動量比的變化包含了液膜、液束入口速度(流動參數)和液膜厚度、液束直徑(結構參數)等的變化,可使研究結果更具一般性地說明動量比這一無量綱參數的影響規律。試驗中選取的可更換液膜厚度h1和液束直徑d的結構參數如表5所示。 表5 試驗中可更換液膜厚度和液束直徑的結構參數表Table 5 Structural parameters of replaceable thickness of liquid sheet and diameter of liquid jet in experiment 試驗系統簡圖如圖10所示,試驗中通過高壓空氣擠壓貯箱實現試驗用水供應,供應管路上設置科氏力質量流量計(型號:F050),測量水的質量流量。試驗中,噴前壓力通過安裝在靠近噴前的壓阻型壓力傳感器測得,采樣頻率1 000 Hz[41-42]。使用LED面光源照射噴注單元及其液霧場,通過Phantom V12.1型COMS黑白高速相機及其鏡頭拍攝噴注單元的撞擊霧化過程圖像,該相機最大分辨率為1 280 pixel×800 pixel,在最高1×106frame/s的幀頻下能達到的最大分辨率為128 pixel ×8 pixel,最小曝光時間1 μs。試驗中觀測方法如圖10所示,高速相機采樣頻率為3 000 Hz,曝光時間為10 μs,圖像分辨率為 1 024 pixel×768 pixel。 圖10 噴嘴霧化試驗系統Fig.10 Spray experiment system for injectors 試驗中噴霧圖像采用高速陰影法拍攝,然而霧化過程是瞬態過程,產生的霧扇會隨時間波動,為了準確評估霧化角大小,對試驗獲得的如圖11(a)所示的噴霧瞬態圖像進行圖像增強處理,獲得如圖11(b)所示的增強圖像,然后將1 000 張增強后的瞬態圖像進行平均處理獲得如圖11(c)所示的圖像,再取霧扇邊界平均中心來測量獲得霧化角,如圖12所示。 圖11 試驗結果圖像處理過程Fig.11 Image processing of experimental results 圖12 試驗測得的霧化角Fig.12 Spray angle of experimental result 針對1.1.3節建立的液膜/液膜撞擊霧化角理論模型中引入的變形因子C1和C2,通過分相識別方法對2路液膜的撞擊霧化過程進行數值仿真,分別提取軸向液膜和徑向液膜撞擊前后的截面面積,如圖13[33]所示,圖中M1in、M2in、M1out和M2out分別為軸向路和徑向路撞擊前后截面的動量,pw為壁面壓力,p2in為徑向路撞擊前截面的壓力,Fw為壁面摩擦阻力。出口截面的統計位置選在撞擊點下游徑向距離4 mm處。通過獲得的2路液膜入口截面面積A1in和A2in及出口截面面積A1out和A2out計算得到的面積比C1和C2如圖14所示。可以看出隨動量比的變化,面積比基本維持在0.9~1.1,特別是動量比小于2.5時,這也是實際應用中動量比的范圍。因此,在計算霧化角時C1和C2在0.9~1.1范圍內取值(推薦值如圖15所示,其是根據霧化角數據擬合獲得,圖中括號里還給出了C1和C2擬合獲得的上限值和下限值),采用推導的霧化角模型可準確預估霧化角。 圖13 液膜撞擊液膜流場結構[33]Fig.13 Flow field structure of liquid sheet impinging on liquid sheet[33] 根據上述獲得的結果,將數值仿真計算的霧化角、根據面積比(變形因子)計算的霧化角、試驗測得的霧化角、以前常用的tan模型預測的霧化角、Cheng的模型(即本文模型對應的C1=1、C2=1特例)預測的霧化角及根據圖15擬合得到的變形因子模型預測的霧化角進行對比,得到如圖16所示的霧化角隨動量比變化曲線,可以看到霧化角隨著動量比增大而增大;在動量比較小時,霧化角增長較快;在動量比較大時,霧化角增長開始變慢;在動量比很大時,霧化角增大很慢。從圖16還可以看出在動量比大范圍變工況下,數值仿真結果、試驗結果及變形因子模型預測結果均吻合很好,與以前常用的tan模型預測結果差異較大,最大相差20°以上,原因已在1.3節中討論分析。另外,發現Cheng的模型也與計算結果及試驗結果吻合較好,這是由于液膜撞擊液膜屬于正撞,僅有正向應力壓縮作用,撞擊過程液膜變形較小,撞擊前后橫截面變化很小,變形因子接近1,圖14和圖15的結果可以印證這點,因而該模型也成立。 圖14 面積比的計算結果Fig.14 Calculation results of area ratio 圖15 霧化角擬合獲得的面積比Fig.15 Fitting curve of area ratio according to spray angle 圖16 不同動量比下的霧化角結果對比(液膜撞擊液膜)Fig.16 Comparison of spray angles at various momentum ratios (liquid sheet impinging on liquid sheet) 相比于液膜撞擊液膜,液膜撞擊液束屬于三維空間撞擊,同時存在正向應力壓縮和切向應力剪切的雙重作用,撞擊過程中液膜與液束均會發生較大變形,液束會同時發生彎曲變形和橫截面變形,液膜也會發生繞液束的分叉流動,因此液膜/液束撞擊的霧化角變化規律與液膜/液膜撞擊的存在差異。根據1.2節建立的液膜/液束撞擊霧化角模型,引入阻塞率定義有效動量比,獲得了霧化角隨有效動量比變化的曲線,如圖17所示。同樣將數值仿真結果、試驗結果、以前常用的tan模型預測結果及變形因子均為1(C1=1、C2=1)的模型預測結果進行對比可以發現,數值仿真結果與試驗結果在有效動量比大范圍變工況下均吻合很好,與變形因子均為1的模型預測結果趨勢一致,與以前常用的tan模型預測結果差異較大,這類似于4.1節液膜與液膜撞擊霧化角的結果。然而進一步對比圖17(a)可以發現,在中等有效動量比(1.2~2.0)下,變形因子均為1的模型(即Cheng模型)預測結果與仿真結果及試驗結果吻合較好;在低的有效動量比(<1.2)下,該模型明顯高估了霧化角;在高的有效動量比(>2.0)下,該模型明顯低估了霧化角。可見,對于膜撞束,由于變形顯著增大,未考慮膜束變形影響的Cheng模型預測值誤差增大,此時該模型適應的局限性凸顯。 對于新模型,根據試驗結果和數值仿真結果擬合變形因子C1和C2得到如圖17(b)所示的結果,在低的有效動量比時,得到的變形因子為C1=0.95和C2=1.05;在高的有效動量比時,得到的變形因子為C1=0.55和C2=1.45;綜合高低有效動量比范圍內的結果,得到的變形因子為C1=0.75和C2=1.25,可以看到在動量比大范圍變工況下,擬合的變形因子模型預測結果與試驗及數值仿真結果均吻合較好。以上結果是在動量比大范圍變工況下獲得的,包含了液膜、液束入口速度(流動參數)和液膜厚度、液束直徑(結構參數)等的變化,因此可使研究結果更具一般性地說明動量比這一無量綱參數的影響規律。 圖17 不同動量比下的霧化角結果對比(液膜撞擊液束)Fig.17 Comparison of spray angles at various momentum ratios (liquid sheet impinging on liquid jet) 圖18 液膜繞液束的流動與變形過程Fig.18 Flow and deformation process of liquid sheet around liquid jet 圖19 液膜與液束撞擊形成的“Ω”形霧扇Fig.19 “Ω” shape spray fan formed by liquid sheet impinging on liquid jet 至此,針對建立的霧化角模型,分析和驗證了引入變形因子的合理性和準確性,也給出了定量預估霧化角建議的變形因子參考值,可為針栓式噴注器的理論研究和工程設計提供重要參考。 為了研究動量比對針栓式噴注器撞擊霧化角的影響規律,從動量守恒方程出發推導建立了液膜撞擊液膜和液膜撞擊液束霧化角的新理論模型,同時基于Gerris開源軟件采用的自適應網格技術和PLIC VOF方法對液膜/液束撞擊的霧化角進行了數值模擬,并結合試驗結果對理論模型進行了驗證。本文研究表明: 1) 基于軸向動量守恒和徑向動量不守恒的假設,通過理論推導引入了2個變形因子,將撞擊的幾何變形效應與霧化角關聯,推導建立了液膜撞擊液膜的霧化角新模型。引入變形因子的理論模型預測值與試驗及數值仿真結果吻合很好;變形因子基本維持在0.9~1.1,根據試驗結果及仿真結果的推薦值為C1=0.99和C2=1.06。 2) 基于液膜撞擊液膜的霧化角分析模型,通過引入阻塞率定義有效撞擊動量比,同時將液膜液束變形的影響隱含考慮在變形因子中,推導建立了液膜撞擊液束的霧化角新模型。引入變形因子和阻塞率的理論模型預測值與試驗及數值仿真結果吻合很好,理論模型和數值仿真模型均得到了有效驗證;根據試驗結果及仿真結果獲得的變形因子推薦值為C1=0.75和C2=1.25。 3) 建立的霧化角新模型根據實際出口的軸向動量(等于入口軸向動量)和合成總動量計算霧化角,隱含考慮了撞擊變形作用的影響,較根據撞擊前入口的軸向動量和合成總動量計算霧化角的常用tan模型預測值準確度顯著提高,這是2種霧化角模型之間的本質區別,為針栓式噴注器的理論研究和工程設計提供了重要參考。
2.2 計算模型


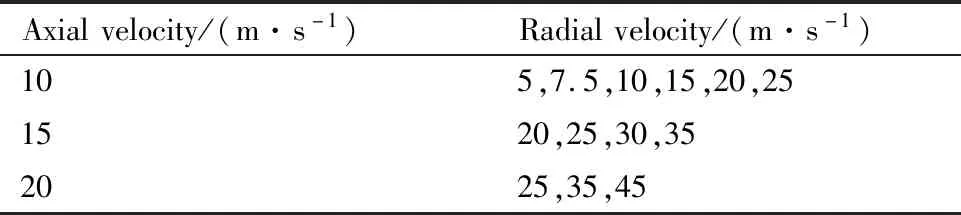



3 噴注單元試驗裝置及試驗測量系統
3.1 噴注單元試驗裝置


3.2 試驗測量系統

3.3 試驗圖像處理方法


4 結果討論與分析
4.1 液膜/液膜撞擊霧化角結果分析




4.2 液膜/液束撞擊霧化角結果分析



5 結 論

