基于分支深度強化學習的非合作目標追逃博弈策略求解

劉冰雁，葉雄兵，高勇，王新波，倪蕾

1.軍事科學院，北京 100091 2.解放軍32032部隊，北京 100094 3.航天工程大學，北京 101416

航天器與非合作目標的空間交會，是最優控制與動態博弈的深度融合，可描述成一種追逃博弈問題[1-3]。從航天器視角看待的追逃博弈(Pursuit and Evasion Hames,PEG)問題[4]，是在僅知自身狀態和非合作目標當前有限狀態、未知非合作目標未來行為策略的條件下，采取最優行為并最終完成交會任務的一個動態博弈過程。

追逃博弈問題中的非合作目標，除了在一個連續且動態變化的空間環境中活動外，還具有典型的非合作性，即有信息層面不溝通、機動行為不配合、先驗知識不完備等特性。針對此類雙方連續動態沖突、對抗博弈問題，可通過微分方程，運用微分對策[5-6]進行數學描述。文獻[7]應用微分對策理論描述了兩個航天器追逃中的策略問題，并將對策研究轉化為高維時變非線性兩點邊值問題進行數值求解。文獻[3]將衛星末端攔截交會看作追蹤與逃逸，并轉換為零和微分對策問題，采用攔截脫靶量和燃料消耗作為二次最優目標函數，推導出了衛星軌道次優控制策略。文獻[8]針對三維空間中的航天器追逃博弈問題展開研究，結合微分對策理論，得出了追蹤器的最優控制策略描述式。文獻[1]利用定量微分對策方法分析連續推力作用下的空間交會追逃微分對策問題，提出了用非線性規劃求解該微分對策問題的方法。文獻[9]對航天器追逃博弈問題運用微分對策進行描述，采用半直接配點法進行求解，可得到收斂的數值解。

關于追逃博弈問題的微分對策求解，因其涉及微分方程復雜、約束條件呈非線性、狀態變量多，一直是一項比較困難而棘手的問題[10-11]。隨著以深度強化學習[12]為代表的新一代人工智能方法快速發展，依其在自主學習、自我優化方面的優勢，處理決策控制問題不受任務模式限制，已在軍事、計算機、交通等領域廣泛運用，并取得了顯著成效[13]。文獻[14]闡述了將深度學習和強化學習為代表的機器學習技術引入博弈對抗建模，提出了基于深度強化學習的智能博弈對抗概念，進一步探索了智能化控制決策。文獻[15]將水面復雜的障礙規避問題轉換為零和博弈問題，提出了一種基于模糊分類的深度強化學習方法，滿足動態決策任務和在線控制過程的需求。文獻[16]針對障礙物動態規避問題，將深度強化學習與優先重放模式相結合，能夠依據經驗對當前狀態進行行為預測，從而降低運算量、提升成功率。文獻[17]為提高準被動雙足機器人斜坡步行穩定性，提出了一種基于深度強化學習的準被動雙足機器人步態控制方法，實現了較大斜坡范圍下的機器人穩定步態控制。

盡管這些研究使得深度強化學習算法在控制決策領域得以應用，但在連續空間應用中仍面臨與表格強化學習相類似的問題，即需要顯式表示的操作數量隨著操作維數的增加呈指數增長。鑒于深度強化學習在控制決策方面的潛力和目前在連續空間的應用限制，針對與非合作目標的空間交會問題，本文提出了一種基于分支深度強化學習的追逃博弈算法，以獲得與空間非合作目標的最優交會策略。

1 航天器與非合作目標的動力學模型

在二體模型中，把中心天體作為參考點，以P表示在軌航天器、E表示非合作目標，兩者空間位置關系如圖1所示。圖中，以同軌道平面內的一參考星作為坐標原點O，參考星與中心天體連線方向為x軸，軌道平面內沿軌道速度方向為y軸，z軸垂直于轉移軌道平面與x軸、y軸構成右手系。航天器與非合作目標相對距離遠小于非合作目標軌道半徑，其動力學模型可描述為

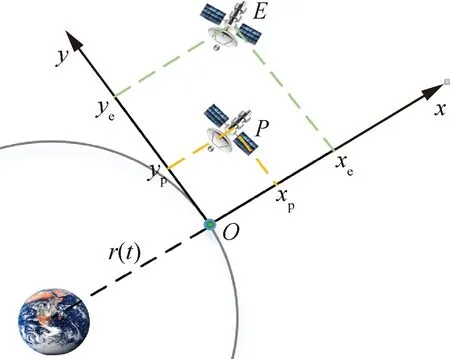
圖1 航天器與非合作目標對策的坐標示意圖Fig.1 Coordinate frame sketch of spacecraft and non-cooperative target

(1)

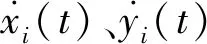
在生存型微分對策[18]中，航天器與非合作目標均采取最大推力，雙方實際行為控制量為推力方向角，即up=[θp,δp]、ue=[θe,δe]。

將航天器與非合作目標的交會問題，描述為追逃博弈問題，需具備以下3個要素：博弈參與者N={P,E}，各參與者行為up、ue，以及參與者的目標函數J。

在追逃博弈的目標函數中，考慮兩者之間的歐式距離

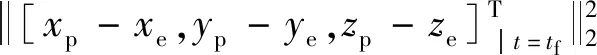
(2)

對于連續推力，燃料消耗與推力作用時間成正比，推力作用時間越長，燃料消耗越多。因此，將推力作用時間間隔作為追逃博弈目標函數的一部分，構建時間-距離綜合最優控制的目標函數

(3)

式中：k為比例權重，且k∈[0,1]。

在追逃博弈過程中，航天器與非合作目標分別根據當前狀態，通過獨立優化目標函數J來采取行為。其間，航天器將力求獲得使目標函數J最小化的行為策略，而非合作目標則期望獲得使目標函數J最大化的行為策略。根據博弈論中的納什均衡[19-20]理論，雙方行為當且僅當滿足不等式(4)時，行為策略達到納什均衡

(4)

為了使該追逃博弈問題存在納什均衡解，假設滿足下列條件：“行為策略集up與ue是度量空間中的緊集，目標函數J：up×ue→R在up×ue上連續”[21]。再根據比較原理[22]可知，若在一個追逃對策中存在不同的最優策略，那么所有最優策略對應的對策值均相同[23]。

由此，求解該追逃博弈問題的目的，就是要尋求一組行為策略滿足納什均衡，即使得式(5)成立

(5)

航天器通過求解上述最優化問題，得到追逃博弈問題的納什均衡行為，從而實現與非合作目標的最優交會。

2 空間行為的模糊推理模型

航天器與非合作目標交會是在連續狀態空間進行，然而傳統的深度強化學習算法可能會由于其難處理性、連續狀態空間和行為空間龐大而導致維數災難問題[24]。為避免這一問題，根據“模糊推理是一種可以任何精度逼近任意非線性函數的萬能逼近器”[25]這一結論，本文構建了一種空間行為的模糊推理模型，以實現連續狀態經由模糊推理再到連續行為輸出的映射轉換，從而有利于發揮深度強化學習的離散行為算法優勢。

零階Takagi-Sugeno-Kang(TSK)[26]，作為最常用的模糊推理模型，在通過隸屬函數(MF)[27]表征連續狀態空間或行為空間后，利用IF-THEN模糊規則可以獲得模糊集到輸出線性函數之間的映射關系[28]：

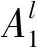
THENul=cl

(6)

圖2展示了當輸入量n=2、隸屬函數y=3時的空間行為模糊推理模型。該模型為5層網狀結構，其中以小圓圈表示變量節點，以小方框表示運算節點。推廣到一般情況，假設有n個連續空間變量xi(i=1,2,…,n)作為輸入，在對每個變量xi運用y個隸屬函數處理后，再經過模糊化與去模糊過程便可獲得精確輸出u，其中各層功能如下所述。

圖2 空間行為的模糊推理模型Fig.2 TSK fuzzy inference model

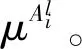
(7)

在網絡第3層，為實現加權平均去模糊化，對隸屬度進行了歸一化處理

(8)

在網絡第4層，引入模糊集中心常數cl，對在每一個節點進行點乘運算

(9)

在網絡第5層，對節點進行累計處理，便可將模糊量轉換成精確量[31]

(10)

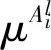
(11)

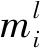
3 追逃博弈的分支深度強化學習

深度強化學習(Deep Reinforcement Learning)，雖是神經網絡與強化學習的有效結合，但直接運用于空間行為模糊推理模型，卻會面臨行為數量與映射規則的組合增長問題，這大大削弱了離散化處理后的行為控制決策能力。此外，值函數的樸素分布以及跨多個獨立函數逼近器的策略表示同樣會遇到許多困難，從而導致收斂問題[32]。

為此，本文提出了一種新的分支深度強化學習架構。將狀態行為值函數的表示形式分布在多個網絡分支上，通過多組并行的神經網絡以實現離散行為的獨立訓練與快速處理；在共享一個行為決策模塊的同時，將狀態行為值函數分解為狀態函數和優勢函數，以實現一種隱式集中協調；給出航天器與非合作目標的博弈交互過程，經過適當的訓練，可實現算法的穩定性和良好策略的收斂性。

3.1 多組并行的網絡分支

依據空間行為模糊推理模型中L條規則，將狀態行為值函數的表示形式分布在多個網絡分支上，搭建L組并行的神經網絡。多組并行的神經網絡，是在單個神經網絡基礎上增加了多組并行神經網絡。與單組神經網絡[33]類似，并行神經網絡在與環境的不斷交互中自主訓練、獨立決策。結合強化學習的博弈和反饋機制，將使得多組并行神經網絡具有更強的自主性、靈活性和協調性，極大地提升了離散行為的獨立學習能力，整體增強了對環境的探索能力。

分支深度強化學習架構中的多組并行神經網絡如圖3所示。其中，各組神經網絡均由輸入層、隱藏層和輸出層組成，當狀態信息分別輸入L組并行神經網絡后，獨立通過激勵函數進行前向傳輸以及進行梯度下降反向訓練，輸出可獲得離散行為的狀態行為函數(簡稱為q函數)。

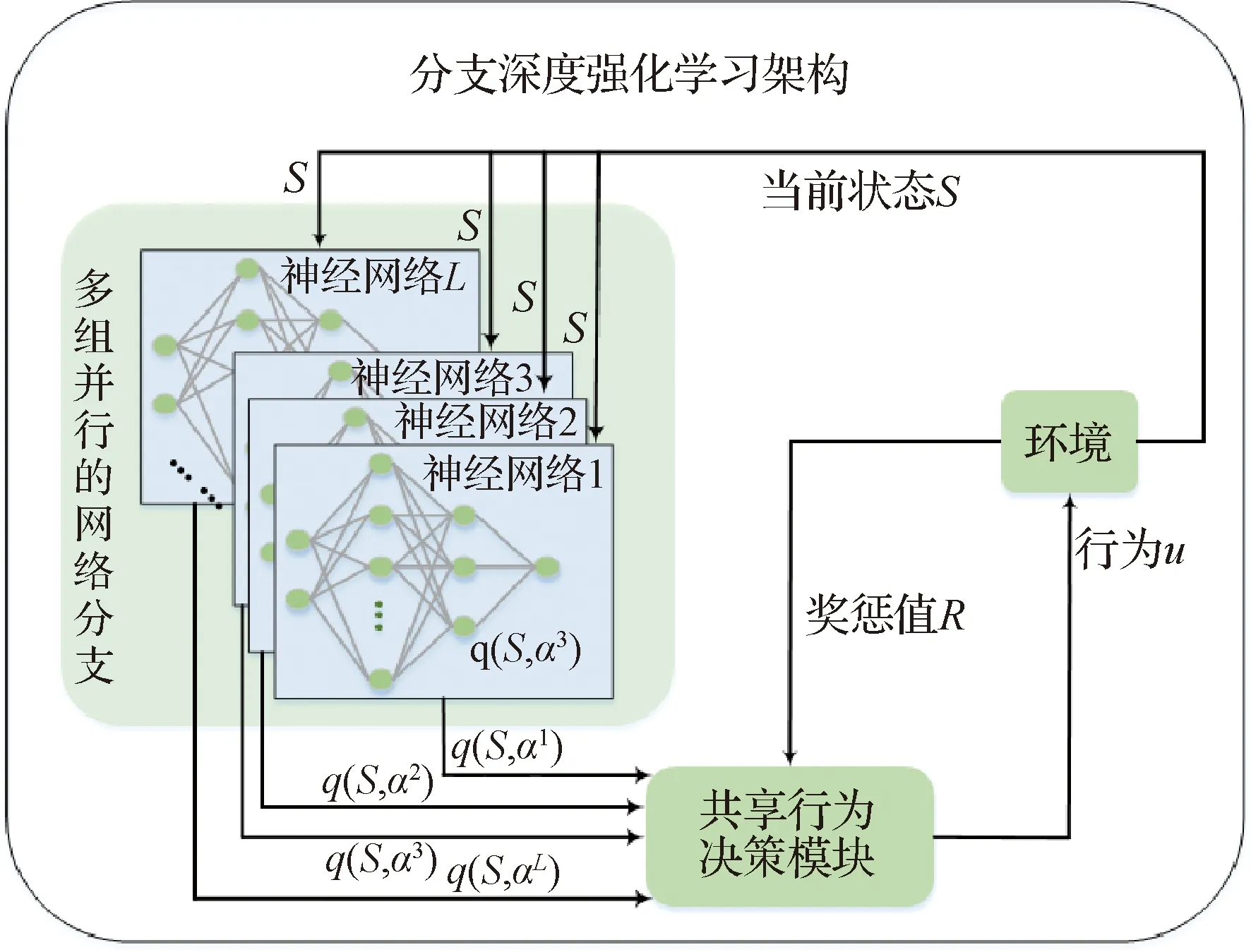
圖3 分支深度強化學習架構示意圖Fig.3 Schematic diagram of branching deep reinforcement learning architecture

3.2 共享行為決策模塊

對于具有n個輸入量和y個隸屬函數的模糊推理模型，直接使用傳統強化學習算法，則需要同時考慮yn個可能的q函數。這使強化學習算法在多離散行為應用中變得棘手，甚至難以有效探索[34]。

本文在所構建的共享行為決策模塊中，對傳統強化學習算法進行了改進。如圖4為基于改進強化學習的共享行為決策示意圖，其主要思想是將多組并行神經網絡計算輸出的q函數分解為狀態函數和優勢函數，以分別評估狀態值和各獨立分支的行為優勢，最后再通過一個特殊的聚合層，將狀態函數和分解后的優勢函數組合起來，輸出得到連續空間行為策略。詳細算法如下所述。

圖4 基于改進強化學習的共享行為決策示意圖Fig.4 Schematic diagram of shared behavior decision based on improved reinforcement learning

在狀態輸入端對模糊規則稍作調整，在空間行為模糊推理模型進行L(L=yn)條IF-THEN模糊規則映射時，用al替換式(6)中的cl，即

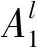
THENul=al

(12)

式中：al為離散行為集a={a1,a2,…,aL}中對應于規則l的行為。

在行為選擇階段，為了有效解決強化學習中的探索與利用問題，即持續使用當前最優策略保持高回報的同時，敢于嘗試一些新的行為以求更大地獎勵，則對行為al采取ε-greedy貪婪策略[15]。該策略定義以ε的概率在離散行為集中隨機選取，以1-ε的概率選擇一個最優行為

(13)

式中：S為當前航天器的位置狀態；q(S,al)為對應規則l和航天器行為al∈a下的q函數。q函數被定義為在ε-greedy策略下從狀態S開始執行行為a之后的期望價值Gt，并將ε-greedy策略下q函數的期望稱為狀態函數[35]

qt(S,al)=E[Gt|St=S,at=a,ε-greedy]

(14)

vt(S)=Ea～ε-greedy[qt(S,al)]

(15)

狀態函數可以度量特定狀態下的行為狀態，而q函數則度量在這種狀態下選擇特定行為的價值。基于此，將q函數與狀態函數的差值定義為優勢函數

ot(S,al)=qt(S,al)-vt(S)

(16)

理論上，優勢函數是將狀態值從q函數中減去后的剩余，從而獲得每個行為重要性的相對度量，并且滿足Ea～ε-greedy[ot(S,al)]=0。然而由于q函數只是對狀態-行為的價值估計，這導致無法明確狀態值和優勢值的估計。為此，利用優勢函數期望值為0這一特性，即當獲取最優行為a*時qt(S,a*)=vt(S)，vt(S)將實現狀態函數的估計，與此同時ot(S,al)亦將實現優勢函數的估計，進而可將q函數分解為一個狀態函數vt(S)和一個優勢函數ot(S,al)

qt(S,al)=vt(S)+

(17)

在行為輸出端，可將與行為選取無關的狀態函數分離出來，只需在對各優勢函數進行優選操作后，再結合式(10)通過全連接層輸出。這一處理既緩解了q函數的運算量，又有效避免了行為數量與映射規則的組合增長問題。

(18)

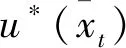
在自主學習階段，在獎懲值的牽引下為實現反饋自主學習，定義時間差分(TD)誤差函數

(19)

式中：γ∈[0,1]為折扣因子；Rt+1為t+1時刻可獲得的獎懲值，并定義Rt+1=2e-u2-1。

q函數更新階段，通過自主迭代訓練進行更新

(20)

式中：η為強化學習速率。

3.3 航天器與非合作目標的博弈交互

將與非合作目標的空間交會問題，經微分策略描述成追逃博弈問題后，運用基于分支深度強化學習的追逃博弈算法，在模糊推理模型中，使得空間連續狀態經由模糊推理以及追逃博弈算法，獲得連續行為輸出。在此以航天器視角為例，展現雙方動態博弈交互過程：

過程1根據航天器當前狀態S定義模糊推理模型輸入量n，設定隸屬函數y。依據模糊規則數，定義L(L=yn)組神經網絡，并對各網絡的q函數進行隨機初始化。

過程3分別在與第l={1,2,…,L}條規則所對應的神經網絡中，計算q函數q(S,al)，根據式(13)選取離散行為al(l=1,2,…,L)。

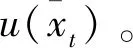
過程5計算航天器與非合作目標的歐氏距離，判斷是否滿足交會條件。若滿足，令變量Done=1并轉到過程10；若不滿足，則轉到過程6。

過程6令變量Done=0，非合作目標根據逃逸策略采取對自己最有利的行為，并移至新位置狀態P+1。

過程7依據行為u以及位置狀態變化情況，計算獎懲值R。在各分支網絡中將當前狀態S、離散行為al、獎懲值R以及下一步狀態S+1，組合成[S,al,R,S+1]矩陣形式并存入記憶庫[35-36]。

過程8共享行為決策模塊中進行自主強化學習，依據式(16)～式(20)，以誤差函數pt為牽引，采取一定的學習率η，更新q函數。

過程9判斷步數是否達到最大行動步數M。若達到，轉至過程10；否則，步數加1并轉入過程2。

過程10結束本輪追逃博弈交互過程。

4 算例分析

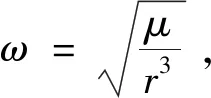
表1 航天器與非合作目標的初始狀態Table 1 Initial state of spacecraft and non-cooperative target

航天器P與非合作目標E之間的空間角度差φ由俯仰角角度差Δδ與軌道平面內推力角之差Δθ構成，即φ=[Δδ,Δθ]

(21)

(22)

式中：φ′為上一狀態的角度差；T是采樣時間。

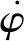
算例仿真在1.6 GHz、1.8 GHz雙核CPU、8GRAM計算硬件上，運用PyCharm仿真編譯環境進行。在分支深度強化學習架構中，考慮離散行為決策無需過多的高維特征信息提取，因此采用的神經網絡層數為3，隱藏層神經元個數為10，激活函數為sigmoid，探索率ε=0.3，折扣因子γ=0.9，學習速率η=0.3，采樣時間T=1 s。

經仿真比對，本文算法具有連續空間行為決策應用的對比優勢。同樣采取ε-greedy策略，分別運用本文算法和傳統深度強化學習算法自主學習1 000次，運用TensorFlow的TensorBoard模塊對學習過程進行檢測，每隔3次對獎懲值進行采樣。圖5為由TensorBoard生成的學習曲線，即獎懲值隨學習次數的累積變化情況。由曲線分布可知，本文算法的獎懲值增長更明顯且更為平穩。

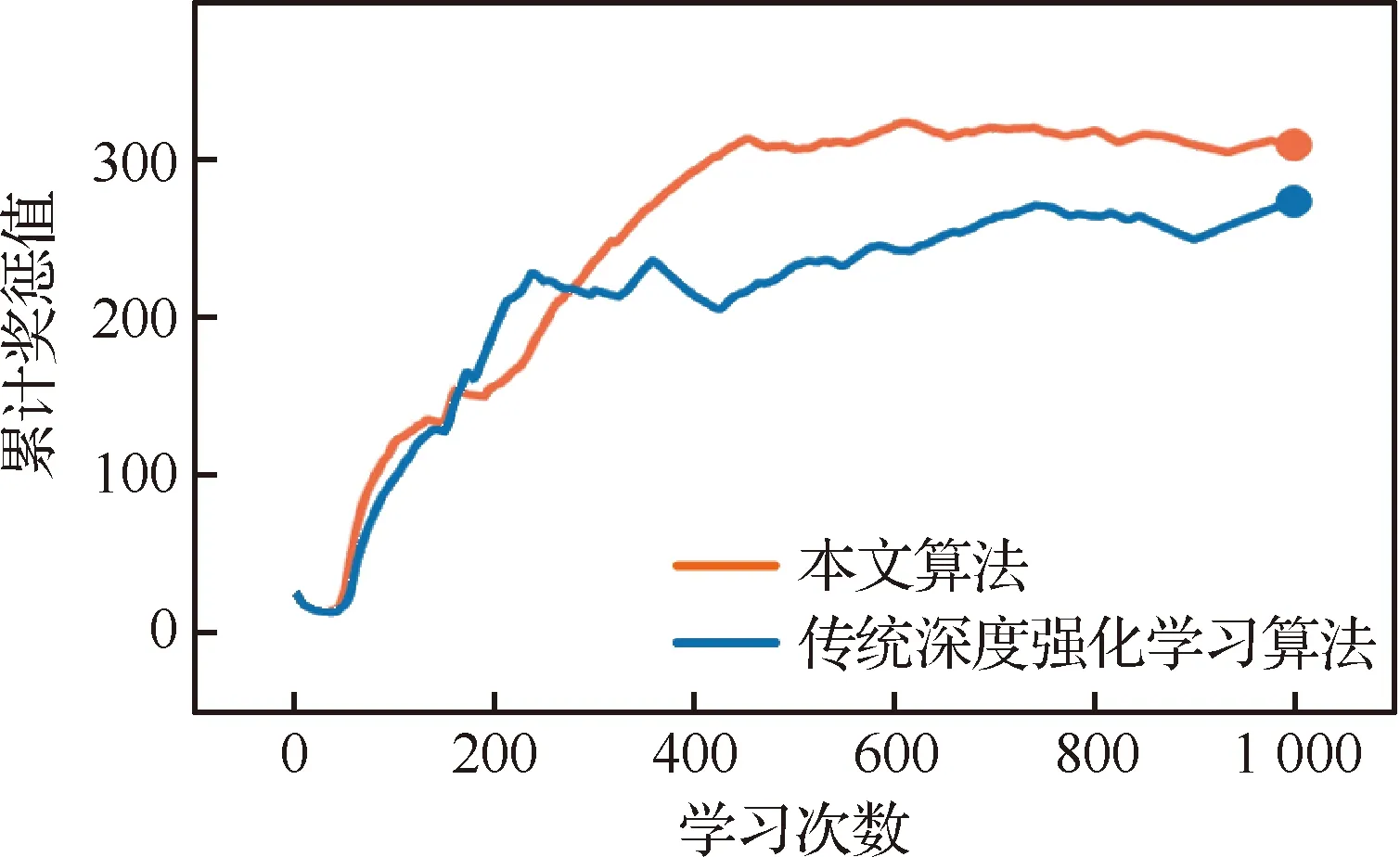
圖5 兩種算法的學習曲線Fig.5 Training curves of two algorithms

算例仿真表明，本文所提算法能夠有效解決航天器與非合作目標的追逃博弈問題。例如，選取經過自主學習0次、500次后的追逃博弈進行比對，其軌跡分別如圖6和圖7所示。圖6為當算法不經學習直接應用于該追逃博弈問題的軌跡變化情況。其中，航天器雖有目標函數驅使，但由于其q函數隨機生成，且沒有任何先驗知識，導致行為舉棋不定、來回浮動，非合作目標不受威脅沿原來軌道方向繼續行進。最終，航天器與非合作目標距離越來越遠，不能完成任務。如圖7所示，當算法經過500次自主學習后，航天器能夠朝著非合作目標方向逼近，途中非合作目標采取規避行為改變既定軌道，雙方不斷博弈在耗時2 328 s后，航天器實現與非合作目標的空間交會。

圖6 學習0次后的追逃博弈軌跡Fig.6 Trajectory of pursuit-evasion game after learning 0 time

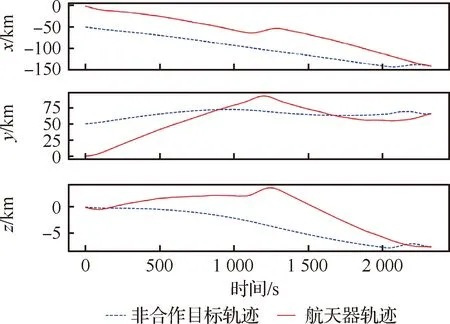
圖7 學習500次后的追逃博弈軌跡Fig.7 Trajectory of pursuit-evasion game after learning 500 times

圖8為自主學習中q函數誤差隨訓練次數的變化情況，隨著訓練次數的不斷增多，q函數誤差越來越低，較快地收斂到最優行為策略，從而實現了該追逃博弈的納什均衡。但由于采用貪婪策略，使得后期誤差還存在微弱的波動。

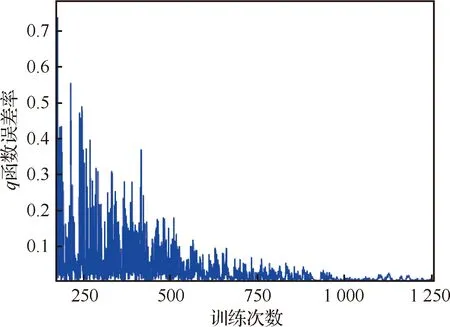
圖8 q函數誤差率隨訓練次數的變化情況Fig.8 Variation rate of q function error with training times

當算法經過1 000次自主學習后，航天器能夠更好地處理非合作目標的逃逸行為，在與非合作目標博弈一段時間后很快使得相互的行為趨于穩定，雙方追逃行為概率分布如圖9所示。依此，在均衡策略的驅使下，航天器能夠選擇最佳軌跡，在最短耗時1 786 s后便與非合作目標實現空間交會，其行為控制量如圖10所示，運動軌跡如圖11所示。由圖易知，雙方在z方向的軌跡沒有發生明顯變化，符合航天器P與非合作目標E在追逃過程中最佳的追逃策略應發生在共面軌道的結論[9,37]。

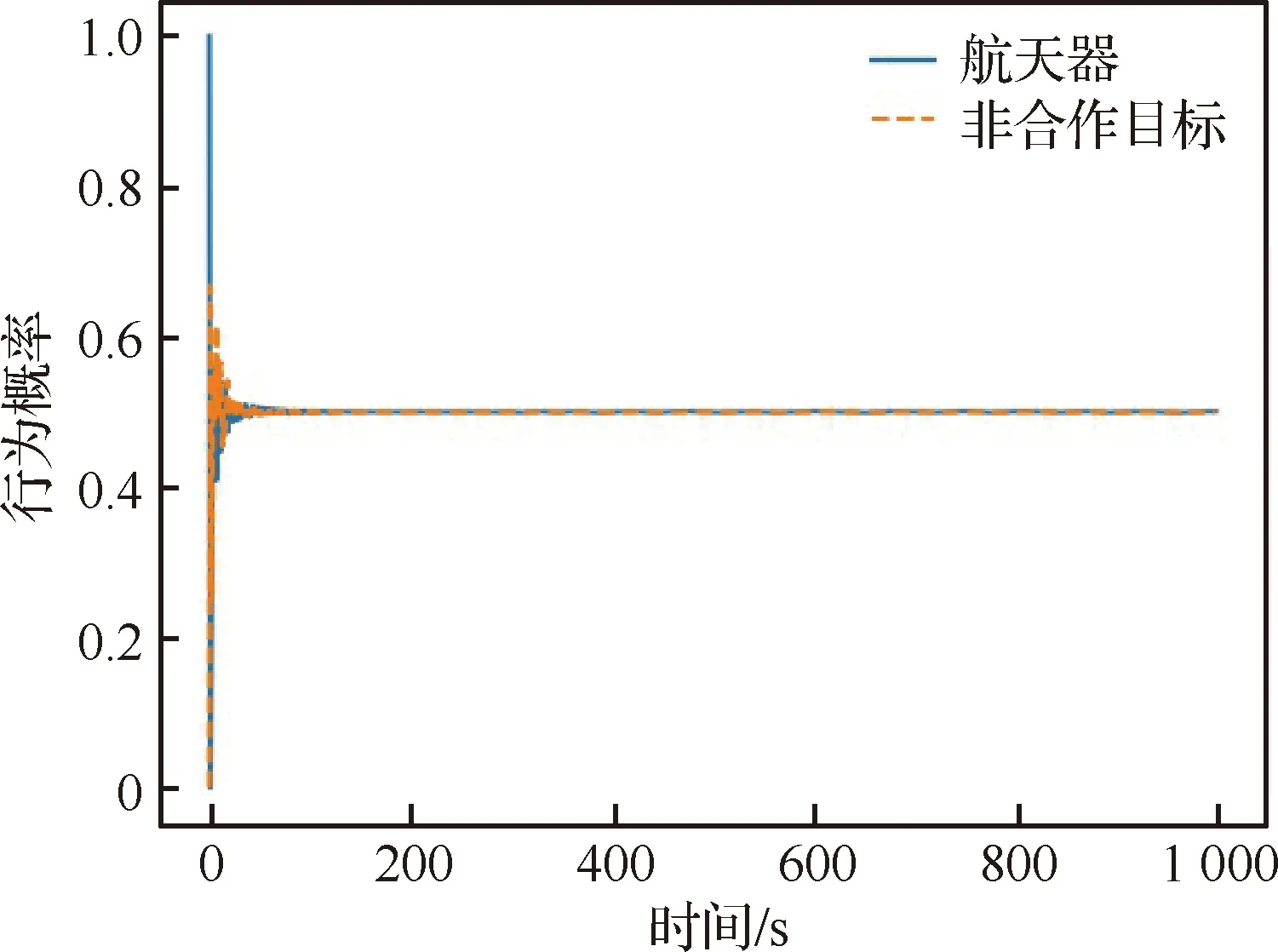
圖9 追逃行為概率分布Fig.9 Probability distribution of pursuit-evasion behavior

圖10 學習1 000次后的行為控制量Fig.10 Amount of behavioral control after learning 1 000 times

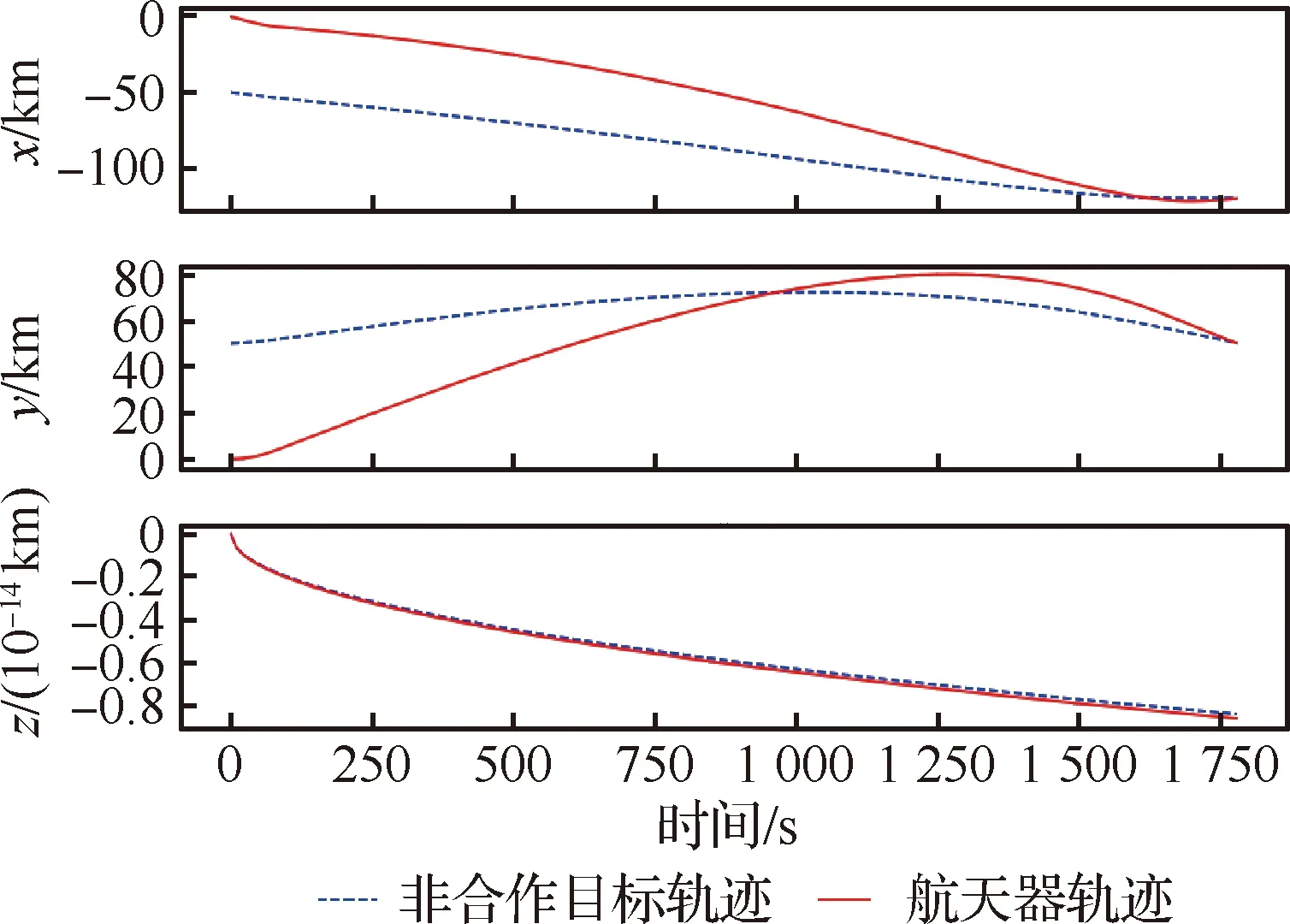
圖11 學習1 000次后的追逃博弈軌跡Fig.11 Trajectory of pursuit-evasion game after learning 1 000 times

5 結 論

1) 構建了近地軌道航天器的追逃運動模型，給出了追逃博弈的納什均衡策略，將非合作目標空間交會策略問題轉述為微分對策問題。

2) 構建了空間行為模糊推理模型，實現了連續狀態經由模糊推理再到連續行為輸出的映射轉換，有效避免了傳統深度強化學習應對連續空間存在的維數災難問題。

3) 提出了一種新的分支深度強化學習架構，實現了行為策略的分支訓練與共享決策，有效解決了行為數量與映射規則的組合增長問題。

算例分析表明，論文算法具有連續空間行為決策應用的對比優勢，能夠有效應對連續空間追逃博弈問題，為非合作目標空間交會策略求解提供了新思路。同時，對于解決其他領域的追逃博弈問題具有較強的借鑒意義。