隧道振動臺試驗相似比試驗設計分析

魏 雯 關振長

（福州大學土木工程學院）

0 引言

我國臨近太平洋地震帶，在高烈度地震頻發的區域，如何確保隧道工程的抗震性能顯得尤為重要，達到“小震不壞，中震可修，大震不倒”的設防目標成為隧道抗震領域亟待解決的熱門問題[1-4]。開展隧道抗震性能的振動臺試驗研究具有重要意義，目前隧道抗震性能研究，主要采用的研究手段為理論分析、原位觀測以及模型試驗[5-9]。模型試驗主要是將模型試驗結果反演到原型結構，進而研究原型結構在地震作用下的變形規律及破壞形態。模型試驗能夠較好的控制邊界條件、模型尺寸以及方便選取地震波類型，進而模擬地震過程[10-12]。

本文依托福州市金雞山隧道擴建項目，通過振動臺試驗分析隧道在地震作用下的變形形態。一個好的模型試驗研究，需要依據相似理論推導出隧道圍巖及襯砌結構的各物理量相似關系。因此，相似比設計在模型試驗中顯得尤為重要，是進行振動臺試驗的理論基礎及前提條件。

1 工程概況

福州金雞山隧道原位擴挖后為雙向8 車道，隧道高13.0m、寬19.0m，隧道最大埋深約39m，隧道圍巖地層由上往下依次為花崗巖殘積砂土、花崗巖殘積粉質粘土與中風化粗粒花崗巖。

考慮到隧道特征及試驗研究目的，選取典型地段，對隧道圍巖土層進行了簡化，簡化后隧道埋深約14m，土層厚度由上往下為12m、15m 和12m。隧道位于花崗巖殘積粉質粘土層，如圖1 所示。

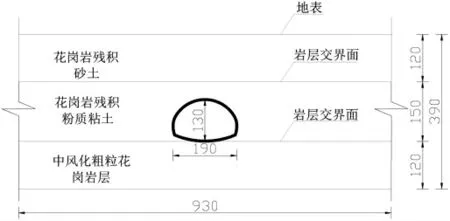
圖1 隧道典型斷面圖（單位：dm）

2 相似理論分析

相似性在自然界中是客觀存在的普遍現象。在幾何相似理論中，對于類似性質的物理過程，假設全部相關的物理量于幾何點和相對時間均存在一定比例關系，則稱之為相似現象。通常認為相似現象遵循一定的物理規律，相似現象采用的物理表達方程式認為是一樣的。相似現象中，原型物理量與對應的縮放物理量的比例關系稱為相似常數，通常情況下，受物理定律的約束相似常數不能隨意選取，例如幾何尺寸最佳相似比是依據重力加速度確定的。當下，確定相似關系主要的方法有方程式與量綱分析[13-14]。

一般情形下，相似判斷若經確定的方程式推導而得，那么用方程分析法推導相似判斷也是準確的。方程分析法建立的基礎是物理過程中每個物理量的函數關系式必須是確定的，但往往受制于試驗條件以及材料的復雜性，很難得到準確的函數關系表達式，此時量綱分析法可以有效的解決這個問題。

通過相似理論分析，每個物理量都存在一定聯系，因此每個物理量之間的量綱也存在一定聯系。

量綱一般是確定物理量的類型種類，無關于量的大小。量綱關系主要是達成一定的量綱和諧，量綱關系主要有以下對應關系：

①假如兩個物理量相等，那么它們數值相等，量綱也相同。②兩物理量若是量綱相同，那么它們的比值是無量綱量的，無關于單位大小。③量綱和諧：一般方程可以采用減、加及等號關聯起來用來描述某一個物理現象，但是每一項的量綱一定要相同。

相似理論是探究物理相似現象的基本原理和指導方法。相似現象一般能夠采用物理方程所表達出來，進而得到三個基本定理如下。

⑴相似第一定理

如果相似指標等于1，則稱為兩個現象相似，那么一樣的物理量所對應點的比例系數相等。1686 年Newton 提出了著名的牛頓準則，較好的闡述了兩個力學系統相似準則問題，同時用相似關系建立了兩個運動物體的關聯問題；1848 年，Bertrand 首次提出了相似第一定理。

⑵相似第二定理

相似第二定律闡述的原理是，當在n 個物理量的某個物理系統中，相互獨立的量綱有m 個，那么存在（n-m）個相似判據。該定理還提出，假設某個物理系統的現象相似，則可以推導出相似判據一樣。1911 經俄國費捷爾曼首次提出；若干年后，被美國學者E.Buckingham 推導論證。

⑶相似第三定理

相似第三定理闡述的原理是，當物理量處于幾何相似系統，那么物理量之間的微分方程要一樣，其中還要求對應部分的模數數值相等。該定理由基爾皮契夫提出。

在相似第三定理中，單值量條件需滿足單個具體現象得從眾多現象中區別篩選出來的條件，它主要包含以下部分：①幾何條件：凡參與物理過程的物體的幾何大小應當給出的單值量條件。②物理條件：在物理系統過程中，物質屬性必須明確單值量條件，主要有泊松比、速度、質量、剪應力、彈模等。③邊界條件：世間物理現象之間均是相互影響的，所以單值量條件在邊界上應當明確，比如：邊界荷載分布情況，地基的支承受力端的方向，分析物體體積膨脹時的溫度條件等。④初始條件：事物現象的發展往往跟初始狀態密切聯系，一般情況下必須給出初始的單值量條件，比如，運動物體的初始速度和出發時間、物體的質量和體積以及自然狀態下物體的溫度等。

各物理量之間是相互聯系的，確定若干個單值量后，通過物理系統中的物理方程式可推導出其他相關單量值。

3 相似比設計

當前受場地及設備的限制，物理模型試驗通常情況是通過原型縮尺進行。根據相似理論，將物理結構原型經相似比設計后縮小進行實驗研究，通過模型試驗研究相關結構的受力規律及破壞形態，進而推導出結構在實際工程應用中的受力情況，以便更好的提供理論基礎支撐及指導工程施工。因此做好模型試驗的重要前提是明確結構的相關物理量以及各物理量之間的相似關系。結合具體的某個試驗，應具體情況具體分析，在物理關系明確，可以用數學函數表達出物理方程式的可采用第三相似定律推導。本文研究的隧道抗震性能分析，其隧道受力關系明確，因此采用方程式推導出各物理量的動力相似關系，進而設計相似比。

3.1 相似關系

模型試驗能否較好的反映實際受力變形情況跟相似關系密切相關。相似關系中提出必須滿足各物理量的相似條件，但通常受制于試驗材料和試驗設備的影響，往往很難做到完全相似。于是，每個試驗項目根據研究的具體目的著重考慮某些物理量相似，進而推導出其他物理量的相似關系。

本項目借助福州某高校振動臺進行了隧道抗震模型試驗研究，其中振動臺的主要物理參數如表1 所示。

表1 振動臺的主要物理參數

通常情況，若是已知三個物理量，且物理量之間相互獨立，那么即可推導出剩余物理量量綱。因此，當沒有離心機時，原型和模型均位于一樣的重力場，要增大物體質量相當困難，重力加速度默認為相等。為了方便模型試驗研究，同時受制于場地和試驗設備，一般假定加速度、幾何尺寸與彈模作為獨立變量，進而依據明確的物理方程式推導剩余的物理量相似比。

通過以上假定，根據具體項目要求、場地條件、材料屬性、經濟條件以及試驗設備，確定出已知量的相似設計比。本項目結合試驗作業臺面以及模型試驗箱，材料吊裝安全等幾方面考慮，最終確定將隧道埋深39m 縮尺為1.3m 較為妥當，進而推導出幾何尺寸相似比為1/30；因在同一重力場，重力加速度相似比確定為1/1；參考已有研究以及材料物理屬性限制，將彈性模量相似比確定1/40。其余物理量相似比通過以上已知條件推導。主要的材料物理量有應變、應力、密度彈模以及泊松比；主要的幾何物理量有位移和幾何尺寸；主要的動力物理量有加頻率、速度、剛度、時間和阻尼等，根據第三相似定律推導后，主要的動力相似關系如表2 所示。

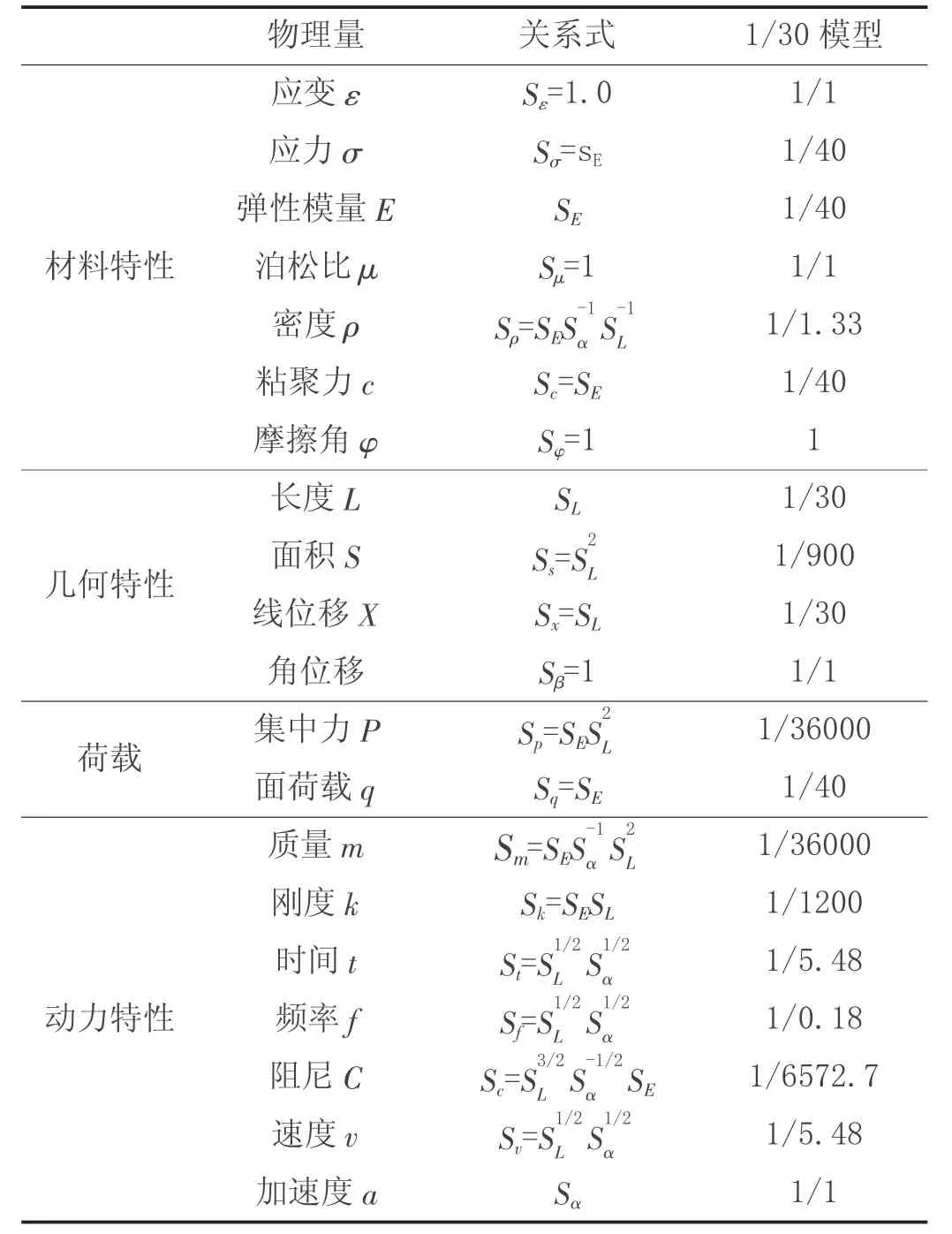
表2 動力相似關系

隧道圍巖相似比設計完成后，襯砌結構的相似比也應確認。從隧道受力角度分析認為，抗彎和彎曲應變對襯砌安全起到重要作用。隧道襯砌結構受力狀態不僅承受抗彎，同時還承受軸力，該襯砌結構類似于圓柱形殼體結構。因此,在模型試驗中我們將抗彎剛度作為研究重點。但是由于隧道結構的軸向和彎曲變形方程不相同，兩者相似準則不能一概而論，應將兩種情況單獨分析考慮。

在隧道結構彎曲變形相似設計中，假設其滿足薄板結構板撓曲ω 控制方程，將薄板厚度設置成h，x 軸與y軸分別為橫截面內的坐標軸，則薄板在橫向均布力q 的作用下，應滿足的薄板撓曲ω 方程如下所示：

式中，

Sh——圍巖長度單位相似比為；

SE——圍巖彈模相似比；

S＇h——二襯長度單位相似比；

S′E——襯砌彈模相似比為。

同時泊松比是無量綱物理量，可推導出S＇μ=Sμ=1。結合本項目試驗目的以及試驗材料屬性，同時便于試驗研究，經過分析對比，將襯砌彈模相似比設置為S′E=SE，進一步推導出S＇h=Sh，那么襯砌結構厚度相似比可以推導出為1/30，襯砌相似關系也如表2 所示。

3.2 確定模型相似尺寸

通過確定長度L 相似比為1/30，重力加速度相似比為1/1，彈性模量相似比確定為1/40，本項目模型試驗的最終尺寸擬定為長310cm、寬80cm 和高130cm。通過相似關系推導，結合表2 的動力相似關系，確定出模型襯砌結構尺寸厚2.5cm、高43cm 以及寬63cm。經過相似設計比，將本項目原型尺寸縮尺后得到的幾何尺寸圖如圖2 所示。縮尺后隧道圍巖劃分為三層，各層厚度由上往下依次為40cm、50cm 以及40cm。

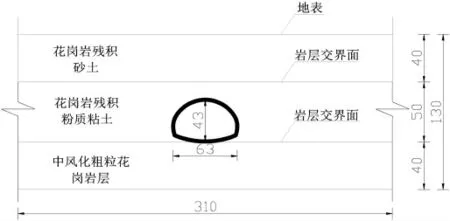
圖2 隧道模型縮尺后立面圖（單位：㎝）

3.3 相似材料選取

由以上相似關系推導可知，模型試驗中采用的材料密度為實際圍巖密度的1.33 倍，因此隧道圍巖底層的中風化粗粒花崗巖，采用巖質相似材料的重晶石粉和鐵粉等模擬；頂層的花崗巖殘積粉質粘土以及底層的花崗巖殘積砂土采用土質相似材料，主要由粉質黏土和膨脹土模擬。在后續振動試驗結果分析中，根據相似比設計反推回實際結構在振動響應中的振動速度、加速度及應力等物理量。通過配合比試驗得到相似材料的主要物理參數盡量滿足表3 的相似關系。

根據相似材料主要物理參數，通過比較分析試驗結果，為了能較好的模擬隧道圍巖物理屬性，本文選取的相似材料配比如下：

⑴花崗巖殘積砂土相似材料配比為：m重晶石粉:m鐵粉:m粉細砂:m松香:m酒精:m石膏=0.606:0.152:0.189:0.033:0.1:0.02。

⑵花崗巖殘積粉質粘土相似材料配比為：m粉質粘土:m重晶石粉:m粉細砂=0.48:0.4:0.12。

⑶砂土狀強風化花崗巖材料配比：m粉質粘土:m重晶石粉:m粉細砂:m膨潤土=0.384:0.32:0.096:0.20。

表3 巖質相似材料的相似關系

4 結語

⑴通過相似比設計，擬定加速度相似比為1/1、幾何尺寸為1/30 以及彈性模量為1/40。確定出模型試驗的最終尺寸擬定為長310㎝、寬80㎝和高130㎝。

⑵通過擬定的物理量相似關系，推導出模型試驗中速度、加速度及密度等其他物理量的動力相似關系。

⑶通過確定隧道圍巖材料的相似比，選取出物理屬性較為適合的材料進行配比作為試驗相似材料。

合理的模型試驗設計，能夠使試驗結果更加真實可靠地反映原型結構變形與受力情況，為隧道抗震研究提供理論基礎。