面向條帶SAR的多孔徑圖像偏移自聚焦算法

李謹成，郭德明

(南京電子技術研究所，江蘇南京 210039)

0 引言

在SAR信號處理中，方位向匹配濾波器的構造精度有賴于對目標斜距歷程的精確計算。對于機載平臺，由于受到大氣湍流、陣風、導航設備不準等多種因素的影響，飛機常常會偏離事先規劃的理想航跡。其結果導致雷達相位中心到目標之間的接收斜距相對于理想狀態發生變化，從而引入回波多普勒信號的相位和幅度誤差，嚴重影響成像質量。因此，機載SAR的數據處理中需要進行運動補償。現階段，由于慣性導航設備的精度達不到亞波長級[1]，基于自聚焦處理的運動誤差估計是獲取高精度機載SAR圖像的關鍵步驟。

多孔徑偏移(Multi Aperture Mapdrift，MAM)算法是一種針對聚束SAR的參數化自聚焦算法[1]：相比于以最小熵算法[2]為代表的參數化自聚焦算法，MAM的誤差模型的階數更高，故其誤差估計精度更高；相比于以相位梯度自聚焦(PGA)[3]為代表的非參數化算法，MAM算法估計的魯棒性更高，能夠在場景缺乏強散射點的情況下準確地估計運動誤差。MAM算法通過測量子孔徑圖像間的位置偏移來估計誤差，由于條帶SAR的雷達波束隨著飛機的運動而運動，其子孔徑圖像對應的場景在不斷變化，因此傳統MAM算法不能直接用于條帶SAR的自聚焦處理。

本文提出了一種能夠用于條帶SAR的多孔徑偏移(Stripmap Multi Aperture Mapdrift，SMAM)算法，在傳統MAM算法的框架下給出針對條帶模式的子孔徑劃分方法、子孔徑成像方法與誤差拼接方法，該方法能夠高精度且魯棒地估計機載條帶SAR的運動誤差，從而獲取高精度的機載SAR圖像。

1 信號模型

機載SAR的觀測幾何模型如圖1所示，Y軸指向載機飛行的方向，Z軸為高度向，X軸與Y軸、Z軸一起構成右手直角坐標系。圖1中的藍色虛線表示事先規劃好的理想航跡，紅色彎曲虛線表示存在運動誤差時載機飛行的實際航跡。當不存在運動誤差時，載機到目標的距離為

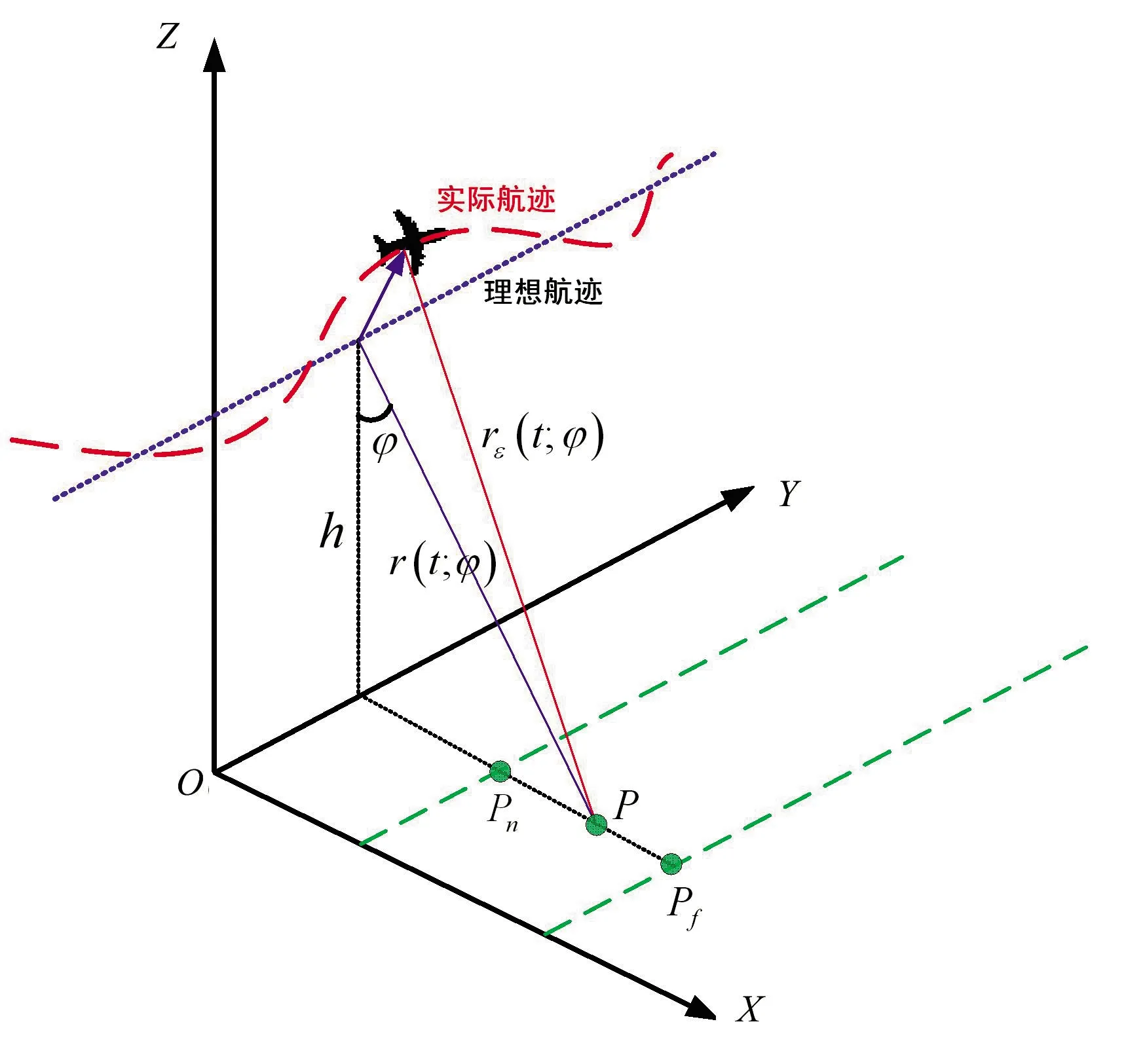
圖1 機載SAR的觀測幾何模型

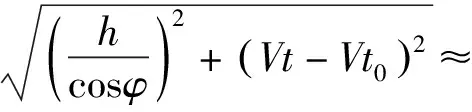
(1)

式中，h為載機的飛行高度，φ為接收機下視角，V為載機的飛行速度，t為方位向時間，t0為載機到目標距離最近的方位向時刻。

當存在運動誤差時，載機到目標的距離為

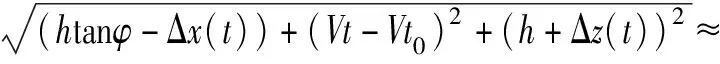
r(t;φ)+ΔrLOS(t;φ)

(2)

式中，Δx(t)和Δz(t)分別為載機在X方向和Z方向上偏離理想航跡的位置誤差，ΔrLOS(t;φ)為接收斜距的誤差，并且

ΔrLOS(t;φ)=Δz(t)·cosφ-Δx(t)·sinφ

(3)

SMAM將運動誤差建模為高階多項式形式，即

(4)

式中，ηm為第m階誤差系數。

2 SMAM算法

2.1 數據分割

為了提高數據處理效率，在SAR的成像處理中每次需要處理多個合成孔徑長度的數據。SMAM算法的第一步是沿方位向分割數據，如圖2所示，SMAM算法中數據分割分為兩步。如圖2(a)所示，SMAM算法首先將數據沿方位向分割為多個估計子塊。如圖2(b)所示，每個SMAM估計子塊之后又被分為多個方位向子孔徑，每個方位向子孔徑對應的時間長度在一秒左右[4]。圖2(b)給出的是子孔徑數目為4時的情況，由于每個SMAM估計子塊的長度小于一個合成孔徑時間，因此每個子孔徑數據對應的場景范圍均有重疊的部分。圖2(b)以第一個子孔徑為例給出了其與其他子孔徑之間的重疊場景(SOL(p,q)表示第p個和第q個子孔徑間重疊場景的長度)，可見重疊場景的方位向長度隨著子孔徑之間距離的增大而減小，而相鄰子孔徑之間的重疊場景范圍最大。

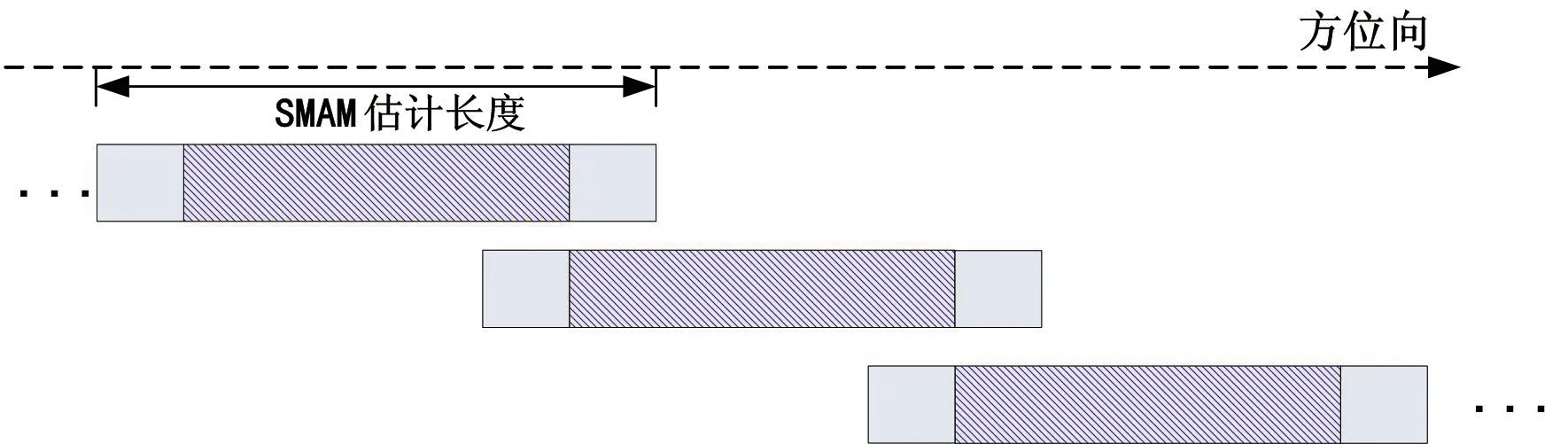
(a)整段數據被分割為多個估計子塊

2.2 子孔徑成像

本文采用后向投影(Back Projection，BP)算法[5]進行子孔徑成像處理，為了使子圖像與信號相位歷程之間有固有的傅里葉變換對的關系，子孔徑成像網格被建立在虛擬極坐標系中[6]。機載虛擬極坐標系的坐標軸為(r,Ξ)，其中Ξ=sinθu，考慮到機載SAR的瞬時多普勒頻率fd=2Vsinθu/λ，λ為雷達波長，因此在機載虛擬極坐標系構建圖像在多普勒頻域是均勻采樣的。另一個坐標軸為距離軸，則可認為子孔徑圖像被構建在距離多普勒域。

2.3 子孔徑圖像互相關處理

在獲取重建在機載虛擬極坐標系的各個子孔徑圖像之后，便可通過互相關處理測量各子圖像之間場景的偏移，進而計算高階多項式誤差模型中的各階系數。圖3給出了條帶模式中子孔徑圖像互相關處理的示意圖，其中位于上方的圖像為基準圖像，位于下方的是被移動圖像。在互相關處理中，被移動圖像沿方位向作圓周位移，然后通過兩幅圖像的幅度相乘得到對應位移下的互相關函數值，即

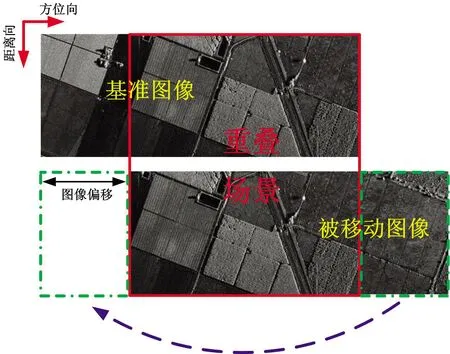
圖3 條帶模式中子孔徑圖像互相關處理示意圖

Cp,q(i)=?Ip(fa,τ;0)·Iq(fa,τ;i)dfadτ

(5)

式中，Iq(fa,τ;i)表示第q個子孔徑圖像沿方位向圓周位移i個像素時的二維幅值函數。

圖4給出了本文第3節所處理真實SAR數據的互相關函數，互相關函數的整體下降趨勢是由于子圖像天線方向圖隨著圓周位移相關性下降造成的。當子圖像間的兩個子圖像的重疊場景處于相同的方位向位置，其互相關函數中會均為出現一個尖峰，圖4中互相關函數的梯度函數如圖5所示，圖5中各梯度函數的最大值和最小值分別對應互相關函數中尖峰兩側的“陡坡”。位于“陡坡”頂端的尖峰是函數的極值，其對應的梯度值為零，所以可以通過測量互相關函數梯度的最大值和最小值之間的零點來自動獲取子圖像間場景的偏移量。以第一幅與第五幅子圖像互相關函數為例，圖4和圖5分別在右上角給出了其互相關函數的尖峰附近以及互相關函數梯度最值之間的零點附近的放大圖，由圖中標出的坐標可見相關函數的尖峰與互相關函數梯度最值之間的零點對應著相同的橫坐標。

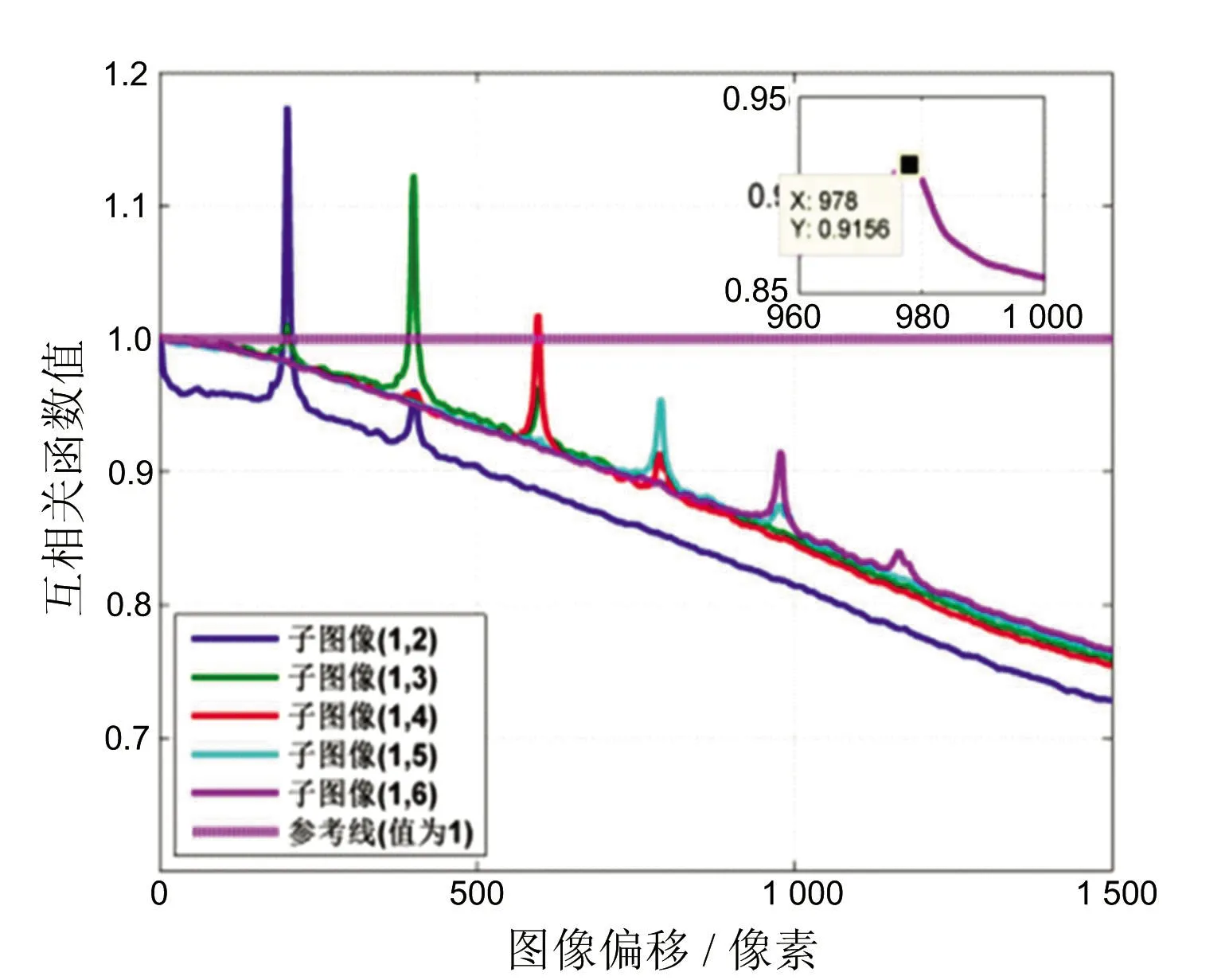
圖4 真實SAR數據的互相關函數

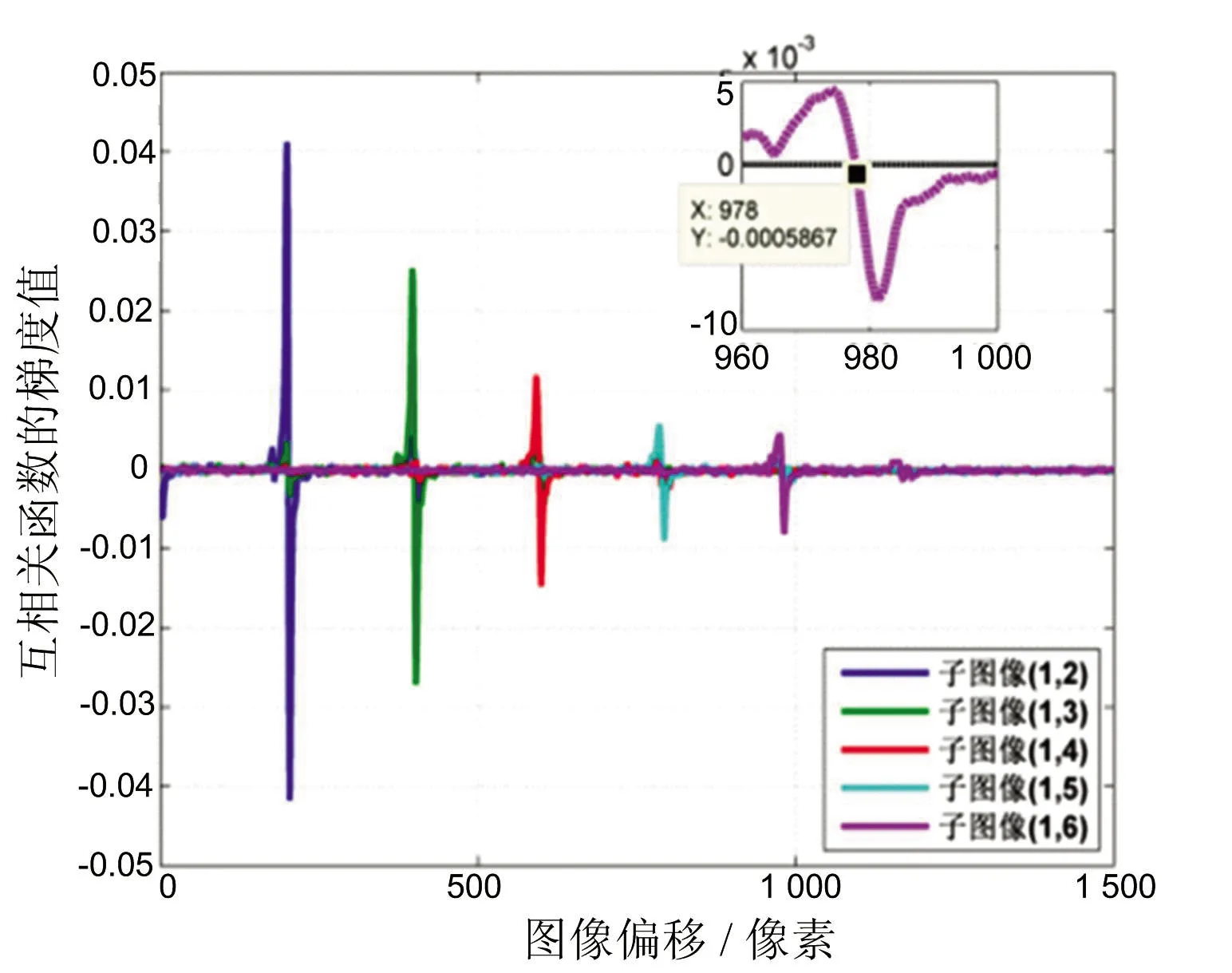
圖5 互相關函數的梯度

2.4 誤差估計與拼接

引起各子孔徑間重疊場景偏移的有兩方面因素。第一個因素為條帶模式下天線波束的移動：當誤差模型的階數設定為M時，在SMAM處理每個估計子塊內的子孔徑數目也為M，則同一目標在第p幅和第q幅(q>p)子圖像間的頻率偏移為

(6)

式中，fr=2V2/λRB為機載SAR方位向調頻率，Tes為估計子塊對應的時間長度。則該頻率偏移在距離多普勒域引起的子圖像偏移為

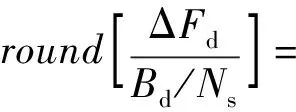
(7)

式中，round[·]表示就近取整操作，Ns為各子圖像方位向采樣點數。

第二個引起場景偏移的因素為載機偏離理想航跡引起的運動誤差：如式(4)所示，在SMAM中運動誤差被建立為高階多項式的形式，則在第p個子孔徑內其對應的相位誤差為

4.控制零食的攝入量及時間，且盡量選擇健康的零食。很多零食盲目的追求口感，而忽略了營養價值，所以要慎重選擇零食種類。零食的攝入不應該影響到正餐，要把握好攝入量及時間。

(8)

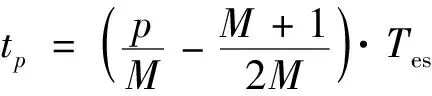
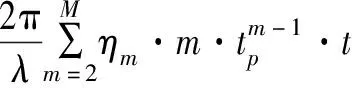
(9)

由傅里葉變換的性質可知，時域的線性相位對應著頻譜的搬移。如前所述，各子孔徑的圖像構建在多普勒域(方位頻域)，則式(9)的時域線性相位在第p幅子圖像內引起的偏移量為

(10)

則由運動誤差引起的第p幅和第q幅圖像之間的相對偏移量為

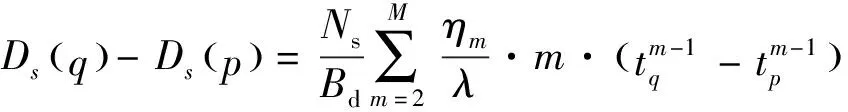
(11)

其中p,q∈[1,2,…,N]，即式(11)能夠包括所有子圖像間的相對偏移量。該表達式能夠寫成下面的矩陣形式[1]：

Δ=δη

(12)

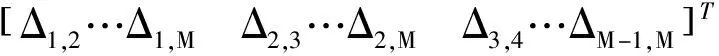
(13)

(14)

(15)

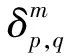
(16)

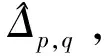
(17)

其中互相關測量得到的偏移矩陣Δ為

(18)

波束移動引起的偏移矩陣Ω為

Ω=[Ω1,2…Ω1,MΩ2,3…Ω2,MΩ3,4…ΩM-1,M]T

(19)

通過解式(12)中的超定線性方程，可得高階誤差多項式的系數的最小二乘解為

ηLs=(δTδ)-1δTΔ

(20)

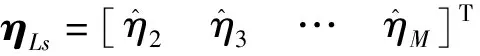
(21)

由于在誤差多項式中不包括線性相位和常數相位，在進行各估計子塊間的誤差拼接處理時需要通過二階求導將式(21)轉換為位置誤差加速度的形式[8]，即

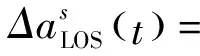
(22)

3 實測數據處理結果

為了驗證所提運動誤差估計方法的有效性，本文選擇一段實測高分辨機載條帶SAR數據進行實驗。該機載SAR系統工作于X波段，工作模式為條帶模式，方位向分辨率為0.2 m，脈沖重復頻率為2 000 Hz，飛機的飛行高度為5 000 m，飛行速度約為100 m/s。該系統所具備的慣導設備精度較低，其絕對精度在米級，遠大于雷達波長(厘米級)，且慣導數據的更新頻率為20 Hz，遠低于系統的脈沖重復頻率。

在高分辨率的機載SAR的自聚焦處理中，誤差估計通常是在子孔徑內進行的，然后進行拼接并在全孔徑補償。因此，子孔徑誤差的估計精度對于獲取聚焦的雷達圖像至關重要。圖6給出了自聚焦處理前后的子孔徑圖像：其中圖6(a)是未經處理的圖像，由于慣導精度較低，圖像散焦嚴重；圖6(b)是PGA算法的處理結果，由于子圖像內缺乏強散射目標，PGA算法不能有效地估計運動誤差；圖6(c)給出的是本文所提的SMAM算法的處理結果，圖中的高壓塔架清晰可見，說明SMAM算法能夠魯棒且高精度地估計運動誤差。

(a)未處理 (b)PGA處理 (c)SMAM處理

圖7給出的是全孔徑數據的處理結果，其中圖7(a)給出的是用慣導數據計算并補償運動誤差后的處理結果，由于慣導設備的精度較低，圖像的整體尤其圖像的左半部分嚴重散焦。圖7(b)給出的是經過SMAM處理后的結果，可見圖像的質量明顯提高，圖像熵由18.626 9降低為17.965 9(圖像熵越小越好)，場景中的屋頂，高壓電線塔架等目標能夠被清楚地分辨出來。

(a)自聚焦處理前

4 結束語

本文所提出的SMAM算法是一種參數化的自聚焦方法，其將運動誤差建立為高階多項式的形式，通過測量各子孔徑圖像內的重疊場景的偏移量來計算高階多項式的系數。由于誤差模型的階數較高，能夠取得比傳統參數化方法更好的估計精度，并且算法對起始輸入的要求較低，能夠魯棒地估計運動誤差。需要注意的是，當運動誤差比較復雜時，高階多項式誤差模型的精度仍然有限，可以再通過如PGA的非參數化處理進一步提高誤差估計的精度。